Learning to Stabilize Unknown LTI Systems on a Single Trajectory under Stochastic Noise
Paper and Code
May 31, 2024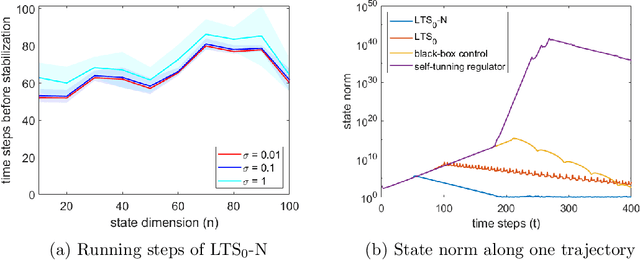


We study the problem of learning to stabilize unknown noisy Linear Time-Invariant (LTI) systems on a single trajectory. It is well known in the literature that the learn-to-stabilize problem suffers from exponential blow-up in which the state norm blows up in the order of $\Theta(2^n)$ where $n$ is the state space dimension. This blow-up is due to the open-loop instability when exploring the $n$-dimensional state space. To address this issue, we develop a novel algorithm that decouples the unstable subspace of the LTI system from the stable subspace, based on which the algorithm only explores and stabilizes the unstable subspace, the dimension of which can be much smaller than $n$. With a new singular-value-decomposition(SVD)-based analytical framework, we prove that the system is stabilized before the state norm reaches $2^{O(k \log n)}$, where $k$ is the dimension of the unstable subspace. Critically, this bound avoids exponential blow-up in state dimension in the order of $\Theta(2^n)$ as in the previous works, and to the best of our knowledge, this is the first paper to avoid exponential blow-up in dimension for stabilizing LTI systems with noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge