Predictive Control and Regret Analysis of Non-Stationary MDP with Look-ahead Information

Policy design in non-stationary Markov Decision Processes (MDPs) is inherently challenging due to the complexities introduced by time-varying system transition and reward, which make it difficult for learners to determine the optimal actions for maximizing cumulative future rewards. Fortunately, in many practical applications, such as energy systems, look-ahead predictions are available, including forecasts for renewable energy generation and demand. In this paper, we leverage these look-ahead predictions and propose an algorithm designed to achieve low regret in non-stationary MDPs by incorporating such predictions. Our theoretical analysis demonstrates that, under certain assumptions, the regret decreases exponentially as the look-ahead window expands. When the system prediction is subject to error, the regret does not explode even if the prediction error grows sub-exponentially as a function of the prediction horizon. We validate our approach through simulations, confirming the efficacy of our algorithm in non-stationary environments.

Autonomous Drifting Based on Maximal Safety Probability Learning

This paper proposes a novel learning-based framework for autonomous driving based on the concept of maximal safety probability. Efficient learning requires rewards that are informative of desirable/undesirable states, but such rewards are challenging to design manually due to the difficulty of differentiating better states among many safe states. On the other hand, learning policies that maximize safety probability does not require laborious reward shaping but is numerically challenging because the algorithms must optimize policies based on binary rewards sparse in time. Here, we show that physics-informed reinforcement learning can efficiently learn this form of maximally safe policy. Unlike existing drift control methods, our approach does not require a specific reference trajectory or complex reward shaping, and can learn safe behaviors only from sparse binary rewards. This is enabled by the use of the physics loss that plays an analogous role to reward shaping. The effectiveness of the proposed approach is demonstrated through lane keeping in a normal cornering scenario and safe drifting in a high-speed racing scenario.

Generalizable Physics-informed Learning for Stochastic Safety-critical Systems

Accurate estimate of long-term risk is critical for safe decision-making, but sampling from rare risk events and long-term trajectories can be prohibitively costly. Risk gradient can be used in many first-order techniques for learning and control methods, but gradient estimate is difficult to obtain using Monte Carlo (MC) methods because the infinitesimal devisor may significantly amplify sampling noise. Motivated by this gap, we propose an efficient method to evaluate long-term risk probabilities and their gradients using short-term samples without sufficient risk events. We first derive that four types of long-term risk probability are solutions of certain partial differential equations (PDEs). Then, we propose a physics-informed learning technique that integrates data and physics information (aforementioned PDEs). The physics information helps propagate information beyond available data and obtain provable generalization beyond available data, which in turn enables long-term risk to be estimated using short-term samples of safe events. Finally, we demonstrate in simulation that the proposed technique has improved sample efficiency, generalizes well to unseen regions, and adapts to changing system parameters.

Learning to Stabilize Unknown LTI Systems on a Single Trajectory under Stochastic Noise

We study the problem of learning to stabilize unknown noisy Linear Time-Invariant (LTI) systems on a single trajectory. It is well known in the literature that the learn-to-stabilize problem suffers from exponential blow-up in which the state norm blows up in the order of $\Theta(2^n)$ where $n$ is the state space dimension. This blow-up is due to the open-loop instability when exploring the $n$-dimensional state space. To address this issue, we develop a novel algorithm that decouples the unstable subspace of the LTI system from the stable subspace, based on which the algorithm only explores and stabilizes the unstable subspace, the dimension of which can be much smaller than $n$. With a new singular-value-decomposition(SVD)-based analytical framework, we prove that the system is stabilized before the state norm reaches $2^{O(k \log n)}$, where $k$ is the dimension of the unstable subspace. Critically, this bound avoids exponential blow-up in state dimension in the order of $\Theta(2^n)$ as in the previous works, and to the best of our knowledge, this is the first paper to avoid exponential blow-up in dimension for stabilizing LTI systems with noise.

Myopically Verifiable Probabilistic Certificates for Safe Control and Learning

This paper addresses the design of safety certificates for stochastic systems, with a focus on ensuring long-term safety through fast real-time control. In stochastic environments, set invariance-based methods that restrict the probability of risk events in infinitesimal time intervals may exhibit significant long-term risks due to cumulative uncertainties/risks. On the other hand, reachability-based approaches that account for the long-term future may require prohibitive computation in real-time decision making. To overcome this challenge involving stringent long-term safety vs. computation tradeoffs, we first introduce a novel technique termed `probabilistic invariance'. This technique characterizes the invariance conditions of the probability of interest. When the target probability is defined using long-term trajectories, this technique can be used to design myopic conditions/controllers with assured long-term safe probability. Then, we integrate this technique into safe control and learning. The proposed control methods efficiently assure long-term safety using neural networks or model predictive controllers with short outlook horizons. The proposed learning methods can be used to guarantee long-term safety during and after training. Finally, we demonstrate the performance of the proposed techniques in numerical simulations.

Physics-informed RL for Maximal Safety Probability Estimation

Accurate risk quantification and reachability analysis are crucial for safe control and learning, but sampling from rare events, risky states, or long-term trajectories can be prohibitively costly. Motivated by this, we study how to estimate the long-term safety probability of maximally safe actions without sufficient coverage of samples from risky states and long-term trajectories. The use of maximal safety probability in control and learning is expected to avoid conservative behaviors due to over-approximation of risk. Here, we first show that long-term safety probability, which is multiplicative in time, can be converted into additive costs and be solved using standard reinforcement learning methods. We then derive this probability as solutions of partial differential equations (PDEs) and propose Physics-Informed Reinforcement Learning (PIRL) algorithm. The proposed method can learn using sparse rewards because the physics constraints help propagate risk information through neighbors. This suggests that, for the purpose of extracting more information for efficient learning, physics constraints can serve as an alternative to reward shaping. The proposed method can also estimate long-term risk using short-term samples and deduce the risk of unsampled states. This feature is in stark contrast with the unconstrained deep RL that demands sufficient data coverage. These merits of the proposed method are demonstrated in numerical simulation.

An Analytic Solution to Covariance Propagation in Neural Networks

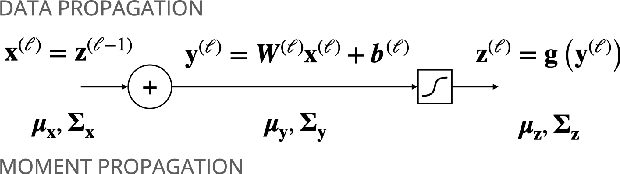
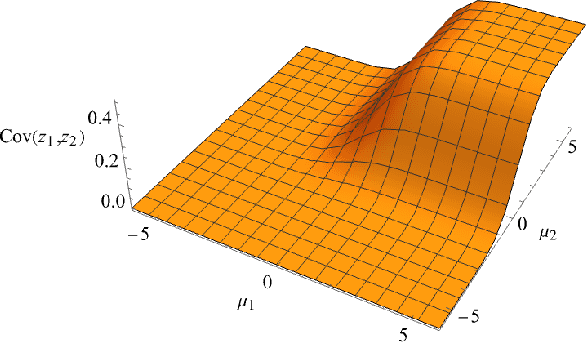
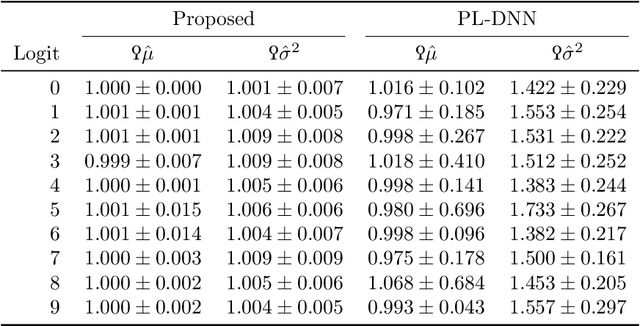
Uncertainty quantification of neural networks is critical to measuring the reliability and robustness of deep learning systems. However, this often involves costly or inaccurate sampling methods and approximations. This paper presents a sample-free moment propagation technique that propagates mean vectors and covariance matrices across a network to accurately characterize the input-output distributions of neural networks. A key enabler of our technique is an analytic solution for the covariance of random variables passed through nonlinear activation functions, such as Heaviside, ReLU, and GELU. The wide applicability and merits of the proposed technique are shown in experiments analyzing the input-output distributions of trained neural networks and training Bayesian neural networks.

Context-aware LLM-based Safe Control Against Latent Risks

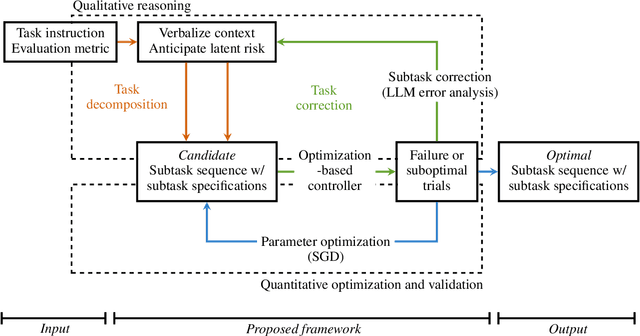
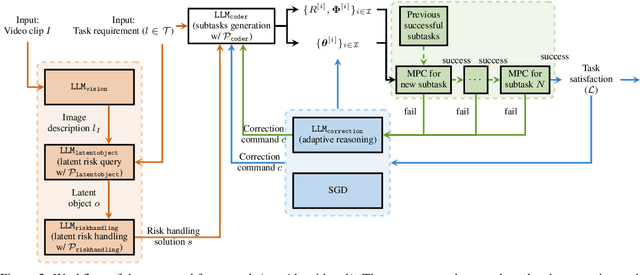
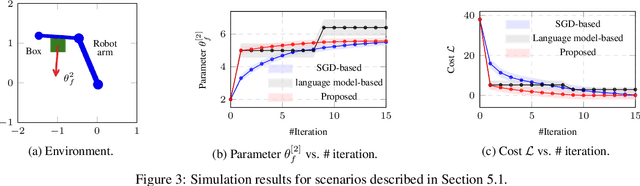
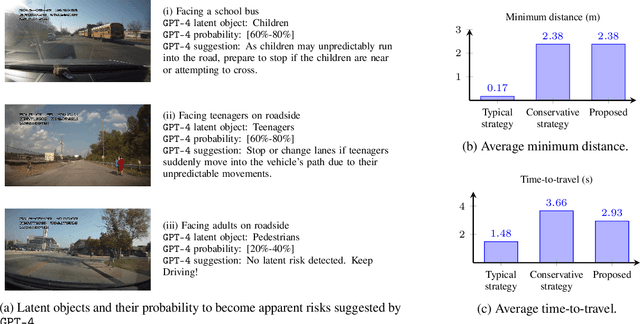
It is challenging for autonomous control systems to perform complex tasks in the presence of latent risks. Motivated by this challenge, this paper proposes an integrated framework that involves Large Language Models (LLMs), stochastic gradient descent (SGD), and optimization-based control. In the first phrase, the proposed framework breaks down complex tasks into a sequence of smaller subtasks, whose specifications account for contextual information and latent risks. In the second phase, these subtasks and their parameters are refined through a dual process involving LLMs and SGD. LLMs are used to generate rough guesses and failure explanations, and SGD is used to fine-tune parameters. The proposed framework is tested using simulated case studies of robots and vehicles. The experiments demonstrate that the proposed framework can mediate actions based on the context and latent risks and learn complex behaviors efficiently.

Towards Proactive Safe Human-Robot Collaborations via Data-Efficient Conditional Behavior Prediction

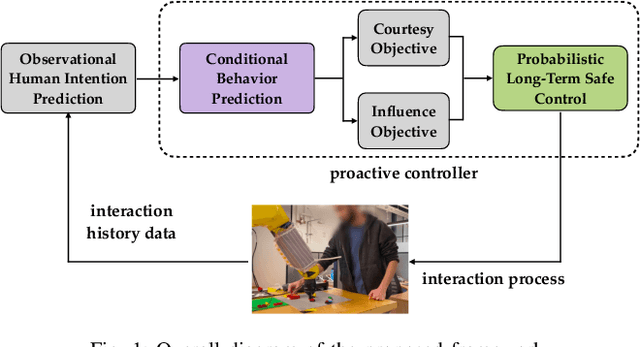
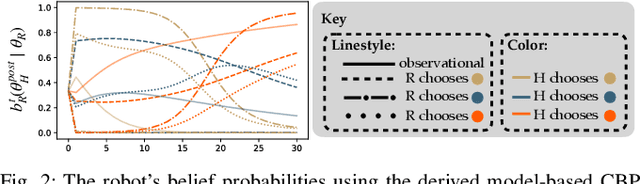
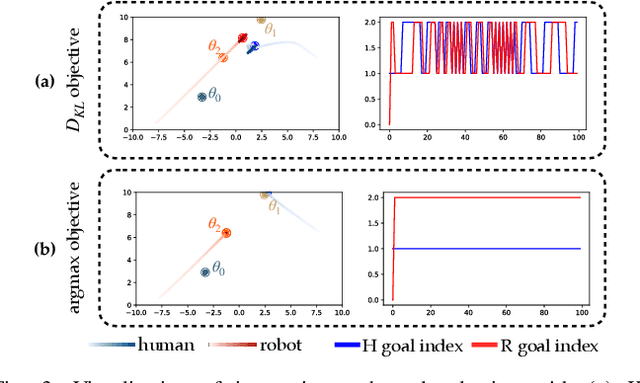
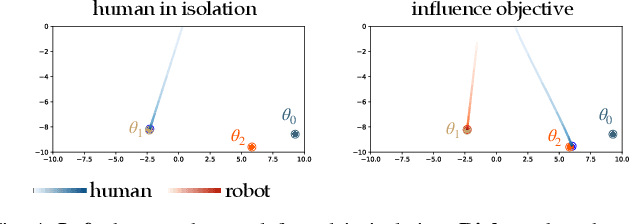
We focus on the problem of how we can enable a robot to collaborate seamlessly with a human partner, specifically in scenarios like collaborative manufacturing where prexisting data is sparse. Much prior work in human-robot collaboration uses observational models of humans (i.e. models that treat the robot purely as an observer) to choose the robot's behavior, but such models do not account for the influence the robot has on the human's actions, which may lead to inefficient interactions. We instead formulate the problem of optimally choosing a collaborative robot's behavior based on a conditional model of the human that depends on the robot's future behavior. First, we propose a novel model-based formulation of conditional behavior prediction that allows the robot to infer the human's intentions based on its future plan in data-sparse environments. We then show how to utilize a conditional model for proactive goal selection and path generation around human collaborators. Finally, we use our proposed proactive controller in a collaborative task with real users to show that it can improve users' interactions with a robot collaborator quantitatively and qualitatively.

A Generalizable Physics-informed Learning Framework for Risk Probability Estimation

Accurate estimates of long-term risk probabilities and their gradients are critical for many stochastic safe control methods. However, computing such risk probabilities in real-time and in unseen or changing environments is challenging. Monte Carlo (MC) methods cannot accurately evaluate the probabilities and their gradients as an infinitesimal devisor can amplify the sampling noise. In this paper, we develop an efficient method to evaluate the probabilities of long-term risk and their gradients. The proposed method exploits the fact that long-term risk probability satisfies certain partial differential equations (PDEs), which characterize the neighboring relations between the probabilities, to integrate MC methods and physics-informed neural networks. We provide theoretical guarantees of the estimation error given certain choices of training configurations. Numerical results show the proposed method has better sample efficiency, generalizes well to unseen regions, and can adapt to systems with changing parameters. The proposed method can also accurately estimate the gradients of risk probabilities, which enables first- and second-order techniques on risk probabilities to be used for learning and control.