Generalizable Physics-informed Learning for Stochastic Safety-critical Systems

Accurate estimate of long-term risk is critical for safe decision-making, but sampling from rare risk events and long-term trajectories can be prohibitively costly. Risk gradient can be used in many first-order techniques for learning and control methods, but gradient estimate is difficult to obtain using Monte Carlo (MC) methods because the infinitesimal devisor may significantly amplify sampling noise. Motivated by this gap, we propose an efficient method to evaluate long-term risk probabilities and their gradients using short-term samples without sufficient risk events. We first derive that four types of long-term risk probability are solutions of certain partial differential equations (PDEs). Then, we propose a physics-informed learning technique that integrates data and physics information (aforementioned PDEs). The physics information helps propagate information beyond available data and obtain provable generalization beyond available data, which in turn enables long-term risk to be estimated using short-term samples of safe events. Finally, we demonstrate in simulation that the proposed technique has improved sample efficiency, generalizes well to unseen regions, and adapts to changing system parameters.

Myopically Verifiable Probabilistic Certificates for Safe Control and Learning

This paper addresses the design of safety certificates for stochastic systems, with a focus on ensuring long-term safety through fast real-time control. In stochastic environments, set invariance-based methods that restrict the probability of risk events in infinitesimal time intervals may exhibit significant long-term risks due to cumulative uncertainties/risks. On the other hand, reachability-based approaches that account for the long-term future may require prohibitive computation in real-time decision making. To overcome this challenge involving stringent long-term safety vs. computation tradeoffs, we first introduce a novel technique termed `probabilistic invariance'. This technique characterizes the invariance conditions of the probability of interest. When the target probability is defined using long-term trajectories, this technique can be used to design myopic conditions/controllers with assured long-term safe probability. Then, we integrate this technique into safe control and learning. The proposed control methods efficiently assure long-term safety using neural networks or model predictive controllers with short outlook horizons. The proposed learning methods can be used to guarantee long-term safety during and after training. Finally, we demonstrate the performance of the proposed techniques in numerical simulations.

DeepCurrents: Learning Implicit Representations of Shapes with Boundaries

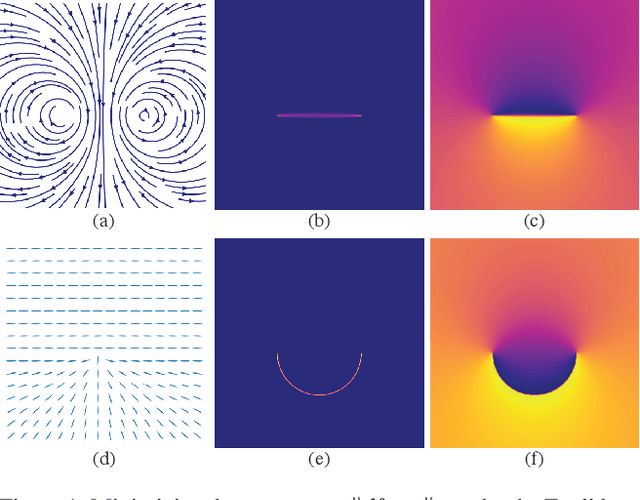
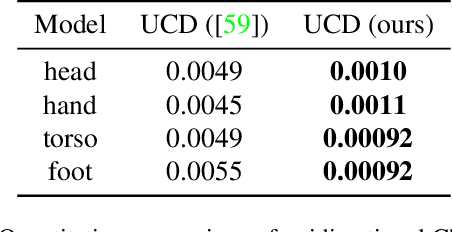
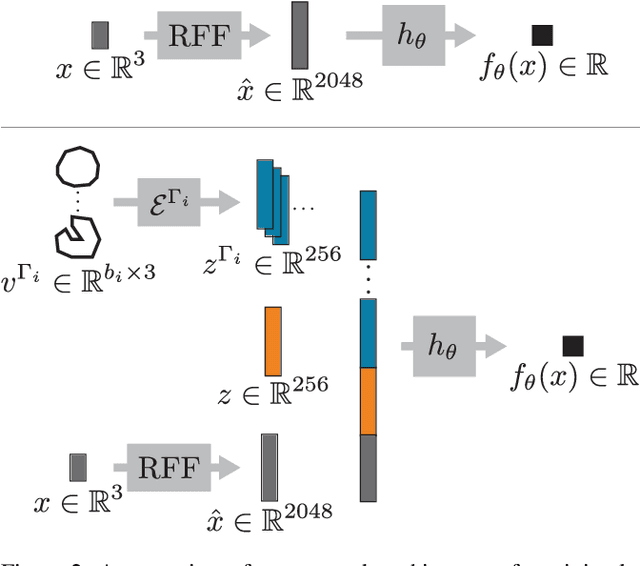
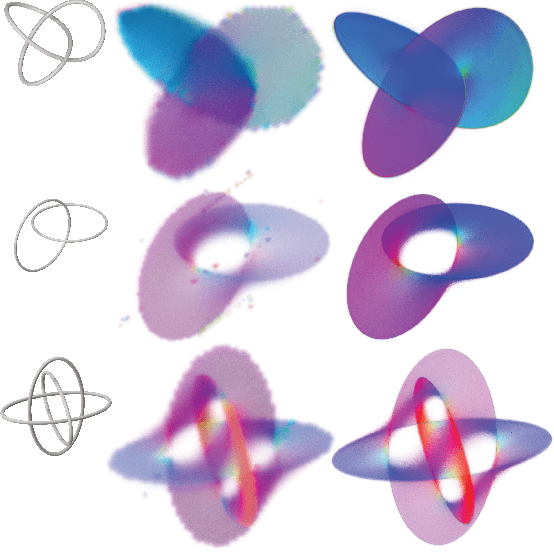
Recent techniques have been successful in reconstructing surfaces as level sets of learned functions (such as signed distance fields) parameterized by deep neural networks. Many of these methods, however, learn only closed surfaces and are unable to reconstruct shapes with boundary curves. We propose a hybrid shape representation that combines explicit boundary curves with implicit learned interiors. Using machinery from geometric measure theory, we parameterize currents using deep networks and use stochastic gradient descent to solve a minimal surface problem. By modifying the metric according to target geometry coming, e.g., from a mesh or point cloud, we can use this approach to represent arbitrary surfaces, learning implicitly defined shapes with explicitly defined boundary curves. We further demonstrate learning families of shapes jointly parameterized by boundary curves and latent codes.

Center of circle after perspective transformation

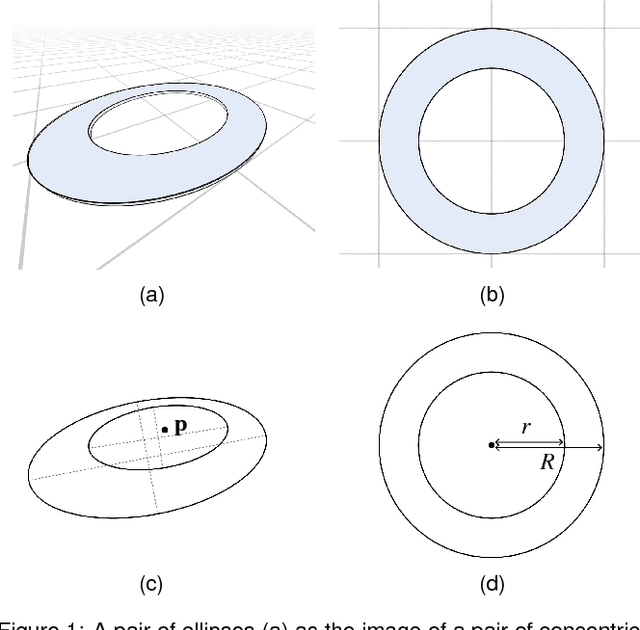
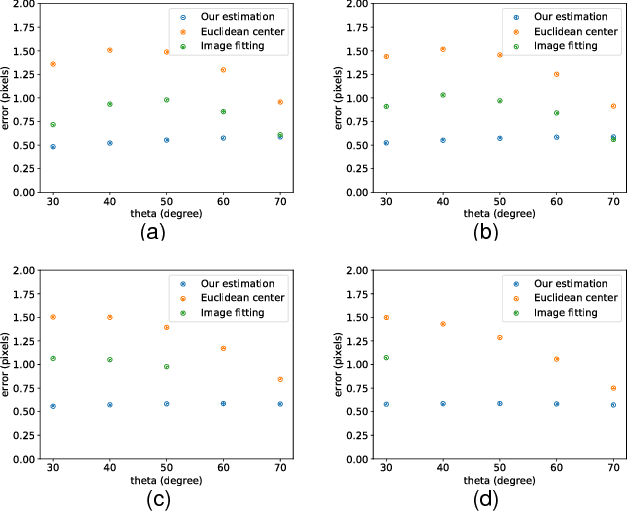
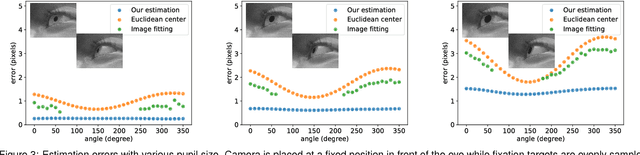
Video-based glint-free eye tracking commonly estimates gaze direction based on the pupil center. The boundary of the pupil is fitted with an ellipse and the euclidean center of the ellipse in the image is taken as the center of the pupil. However, the center of the pupil is generally not mapped to the center of the ellipse by the projective camera transformation. This error resulting from using a point that is not the true center of the pupil directly affects eye tracking accuracy. We investigate the underlying geometric problem of determining the center of a circular object based on its projective image. The main idea is to exploit two concentric circles -- in the application scenario these are the pupil and the iris. We show that it is possible to computed the center and the ratio of the radii from the mapped concentric circles with a direct method that is fast and robust in practice. We evaluate our method on synthetically generated data and find that it improves systematically over using the center of the fitted ellipse. Apart from applications of eye tracking we estimate that our approach will be useful in other tracking applications.