David Palmer
DeepCurrents: Learning Implicit Representations of Shapes with Boundaries
Nov 17, 2021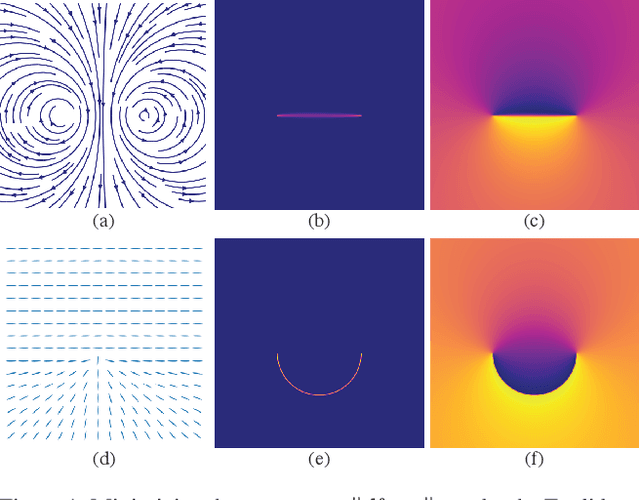
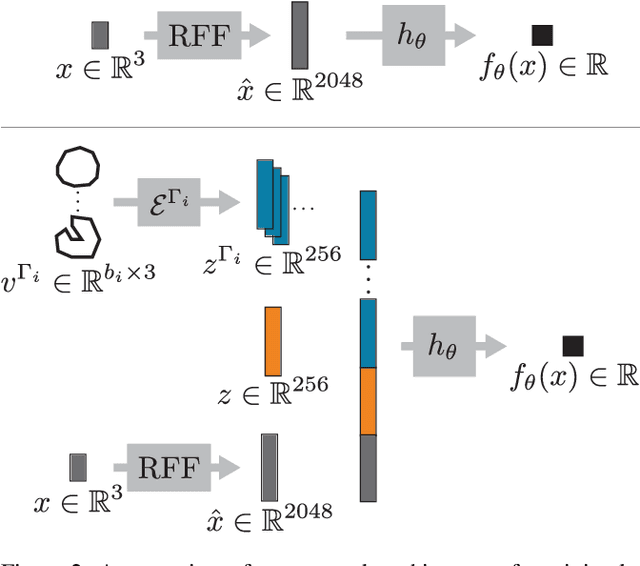
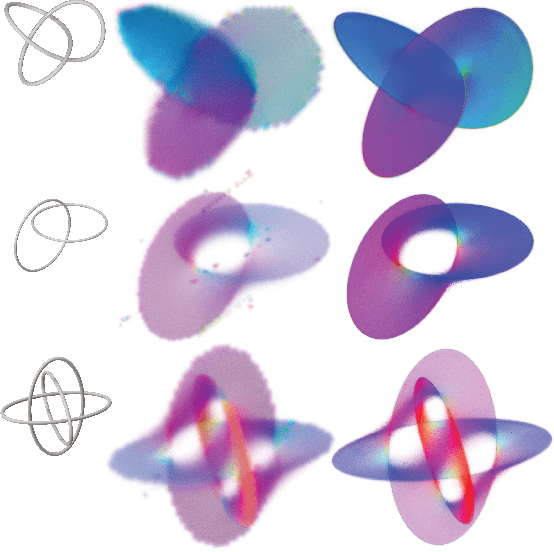
Abstract:Recent techniques have been successful in reconstructing surfaces as level sets of learned functions (such as signed distance fields) parameterized by deep neural networks. Many of these methods, however, learn only closed surfaces and are unable to reconstruct shapes with boundary curves. We propose a hybrid shape representation that combines explicit boundary curves with implicit learned interiors. Using machinery from geometric measure theory, we parameterize currents using deep networks and use stochastic gradient descent to solve a minimal surface problem. By modifying the metric according to target geometry coming, e.g., from a mesh or point cloud, we can use this approach to represent arbitrary surfaces, learning implicitly defined shapes with explicitly defined boundary curves. We further demonstrate learning families of shapes jointly parameterized by boundary curves and latent codes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge