Differentiable Shadow Mapping for Efficient Inverse Graphics

We show how shadows can be efficiently generated in differentiable rendering of triangle meshes. Our central observation is that pre-filtered shadow mapping, a technique for approximating shadows based on rendering from the perspective of a light, can be combined with existing differentiable rasterizers to yield differentiable visibility information. We demonstrate at several inverse graphics problems that differentiable shadow maps are orders of magnitude faster than differentiable light transport simulation with similar accuracy -- while differentiable rasterization without shadows often fails to converge.

Center of circle after perspective transformation

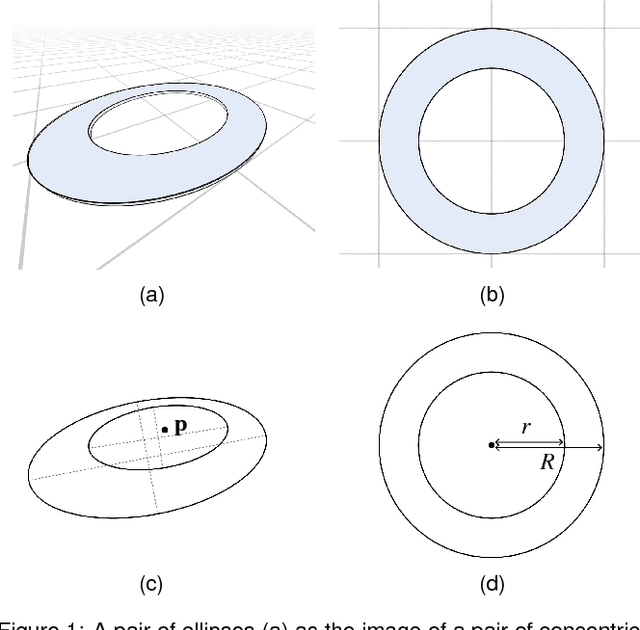
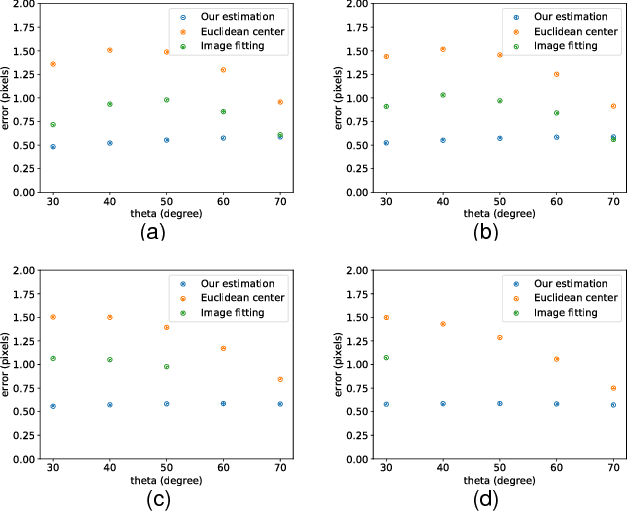
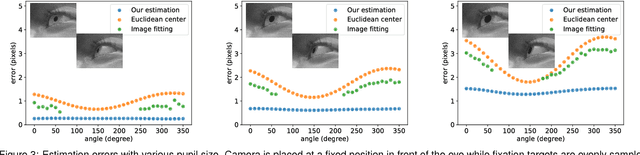
Video-based glint-free eye tracking commonly estimates gaze direction based on the pupil center. The boundary of the pupil is fitted with an ellipse and the euclidean center of the ellipse in the image is taken as the center of the pupil. However, the center of the pupil is generally not mapped to the center of the ellipse by the projective camera transformation. This error resulting from using a point that is not the true center of the pupil directly affects eye tracking accuracy. We investigate the underlying geometric problem of determining the center of a circular object based on its projective image. The main idea is to exploit two concentric circles -- in the application scenario these are the pupil and the iris. We show that it is possible to computed the center and the ratio of the radii from the mapped concentric circles with a direct method that is fast and robust in practice. We evaluate our method on synthetically generated data and find that it improves systematically over using the center of the fitted ellipse. Apart from applications of eye tracking we estimate that our approach will be useful in other tracking applications.

ABC: A Big CAD Model Dataset For Geometric Deep Learning

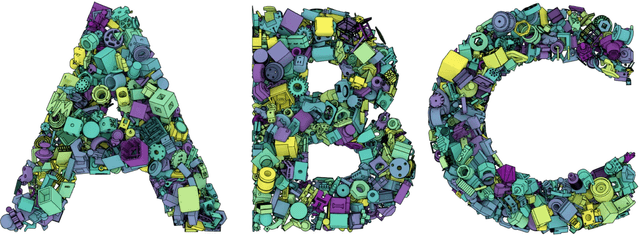
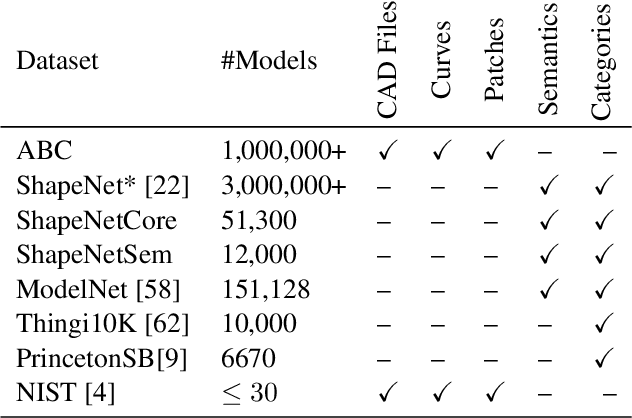
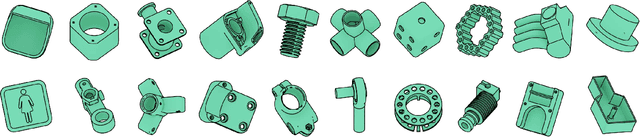
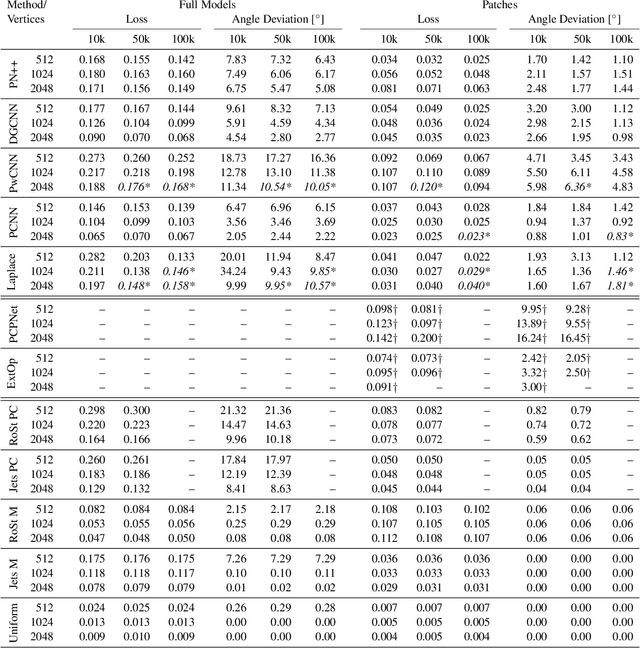
We introduce ABC-Dataset, a collection of one million Computer-Aided Design (CAD) models for research of geometric deep learning methods and applications. Each model is a collection of explicitly parametrized curves and surfaces, providing ground truth for differential quantities, patch segmentation, geometric feature detection, and shape reconstruction. Sampling the parametric descriptions of surfaces and curves allows generating data in different formats and resolutions, enabling fair comparisons for a wide range of geometric learning algorithms. As a use case for our dataset, we perform a large-scale benchmark for estimation of surface normals, comparing existing data driven methods and evaluating their performance against both the ground truth and traditional normal estimation methods.