3D Parametric Wireframe Extraction Based on Distance Fields

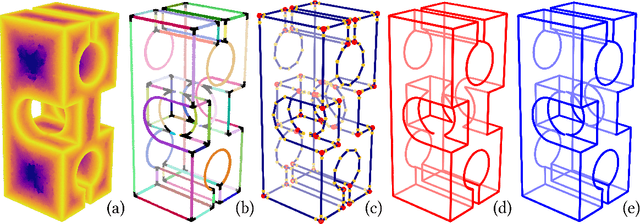
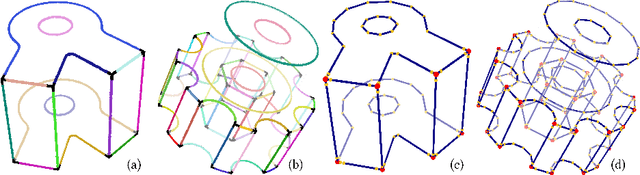
We present a pipeline for parametric wireframe extraction from densely sampled point clouds. Our approach processes a scalar distance field that represents proximity to the nearest sharp feature curve. In intermediate stages, it detects corners, constructs curve segmentation, and builds a topological graph fitted to the wireframe. As an output, we produce parametric spline curves that can be edited and sampled arbitrarily. We evaluate our method on 50 complex 3D shapes and compare it to the novel deep learning-based technique, demonstrating superior quality.

DEF: Deep Estimation of Sharp Geometric Features in 3D Shapes

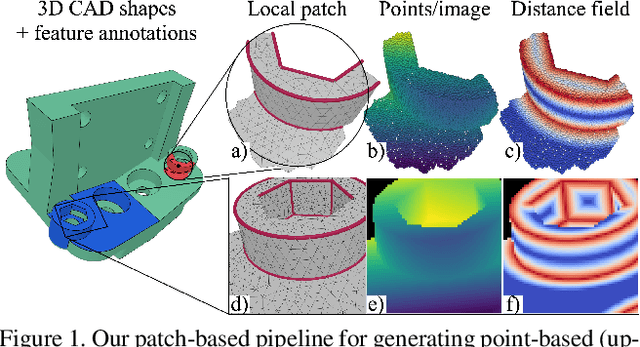
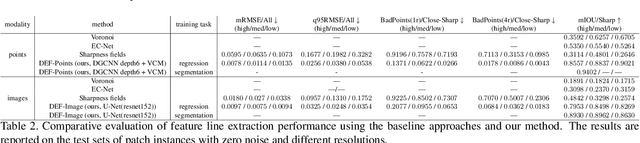
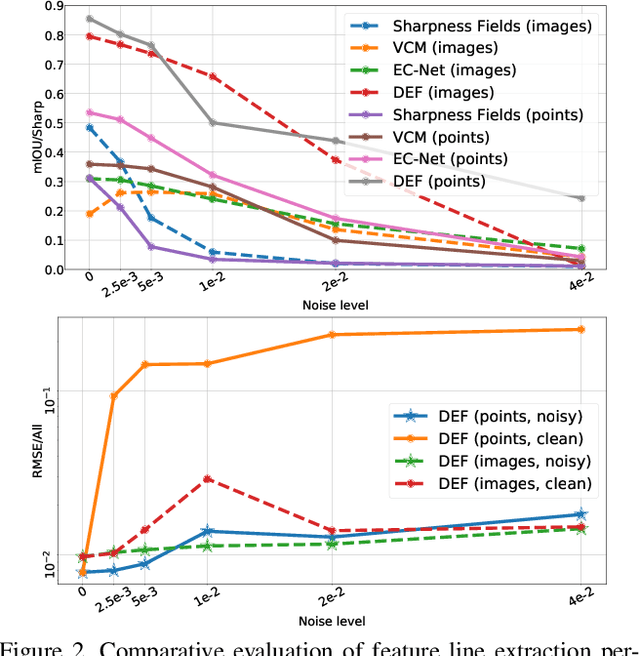
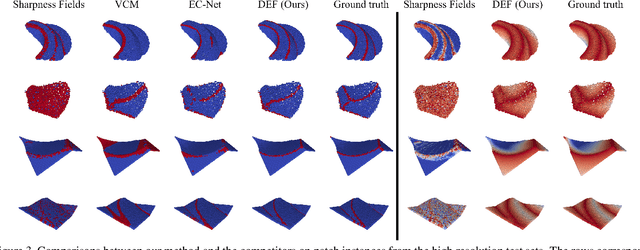
Sharp feature lines carry essential information about human-made objects, enabling compact 3D shape representations, high-quality surface reconstruction, and are a signal source for mesh processing. While extracting high-quality lines from noisy and undersampled data is challenging for traditional methods, deep learning-powered algorithms can leverage global and semantic information from the training data to aid in the process. We propose Deep Estimators of Features (DEFs), a learning-based framework for predicting sharp geometric features in sampled 3D shapes. Differently from existing data-driven methods, which reduce this problem to feature classification, we propose to regress a scalar field representing the distance from point samples to the closest feature line on local patches. By fusing the result of individual patches, we can process large 3D models, which are impossible to process for existing data-driven methods due to their size and complexity. Extensive experimental evaluation of DEFs is implemented on synthetic and real-world 3D shape datasets and suggests advantages of our image- and point-based estimators over competitor methods, as well as improved noise robustness and scalability of our approach.

Geometric Attention for Prediction of Differential Properties in 3D Point Clouds

Estimation of differential geometric quantities in discrete 3D data representations is one of the crucial steps in the geometry processing pipeline. Specifically, estimating normals and sharp feature lines from raw point cloud helps improve meshing quality and allows us to use more precise surface reconstruction techniques. When designing a learnable approach to such problems, the main difficulty is selecting neighborhoods in a point cloud and incorporating geometric relations between the points. In this study, we present a geometric attention mechanism that can provide such properties in a learnable fashion. We establish the usefulness of the proposed technique with several experiments on the prediction of normal vectors and the extraction of feature lines.

Learning to Approximate Directional Fields Defined over 2D Planes

Reconstruction of directional fields is a need in many geometry processing tasks, such as image tracing, extraction of 3D geometric features, and finding principal surface directions. A common approach to the construction of directional fields from data relies on complex optimization procedures, which are usually poorly formalizable, require a considerable computational effort, and do not transfer across applications. In this work, we propose a deep learning-based approach and study the expressive power and generalization ability.

ABC: A Big CAD Model Dataset For Geometric Deep Learning

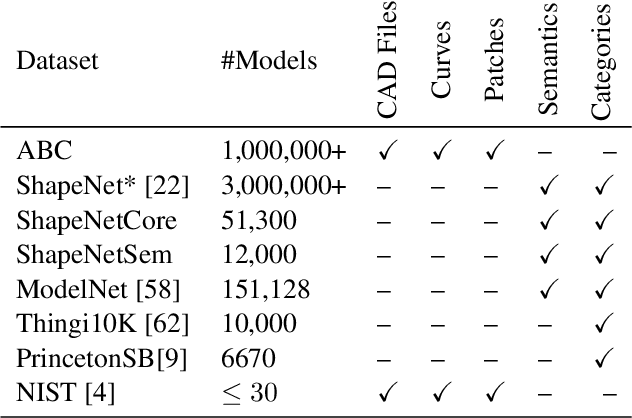
We introduce ABC-Dataset, a collection of one million Computer-Aided Design (CAD) models for research of geometric deep learning methods and applications. Each model is a collection of explicitly parametrized curves and surfaces, providing ground truth for differential quantities, patch segmentation, geometric feature detection, and shape reconstruction. Sampling the parametric descriptions of surfaces and curves allows generating data in different formats and resolutions, enabling fair comparisons for a wide range of geometric learning algorithms. As a use case for our dataset, we perform a large-scale benchmark for estimation of surface normals, comparing existing data driven methods and evaluating their performance against both the ground truth and traditional normal estimation methods.