Evaluating Deep Clustering Algorithms on Non-Categorical 3D CAD Models

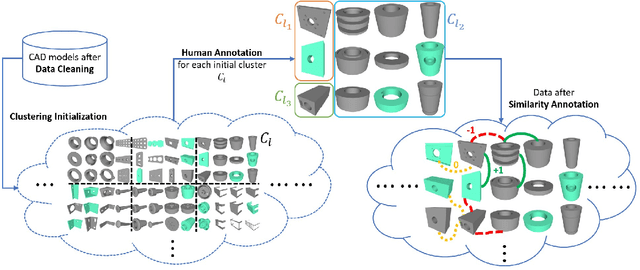
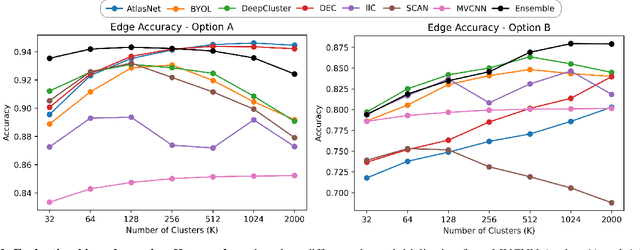
We introduce the first work on benchmarking and evaluating deep clustering algorithms on large-scale non-categorical 3D CAD models. We first propose a workflow to allow expert mechanical engineers to efficiently annotate 252,648 carefully sampled pairwise CAD model similarities, from a subset of the ABC dataset with 22,968 shapes. Using seven baseline deep clustering methods, we then investigate the fundamental challenges of evaluating clustering methods for non-categorical data. Based on these challenges, we propose a novel and viable ensemble-based clustering comparison approach. This work is the first to directly target the underexplored area of deep clustering algorithms for 3D shapes, and we believe it will be an important building block to analyze and utilize the massive 3D shape collections that are starting to appear in deep geometric computing.

Image Sculpting: Precise Object Editing with 3D Geometry Control

We present Image Sculpting, a new framework for editing 2D images by incorporating tools from 3D geometry and graphics. This approach differs markedly from existing methods, which are confined to 2D spaces and typically rely on textual instructions, leading to ambiguity and limited control. Image Sculpting converts 2D objects into 3D, enabling direct interaction with their 3D geometry. Post-editing, these objects are re-rendered into 2D, merging into the original image to produce high-fidelity results through a coarse-to-fine enhancement process. The framework supports precise, quantifiable, and physically-plausible editing options such as pose editing, rotation, translation, 3D composition, carving, and serial addition. It marks an initial step towards combining the creative freedom of generative models with the precision of graphics pipelines.

An Extensible Benchmark Suite for Learning to Simulate Physical Systems

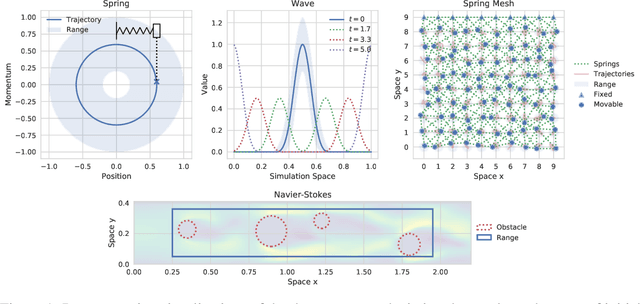
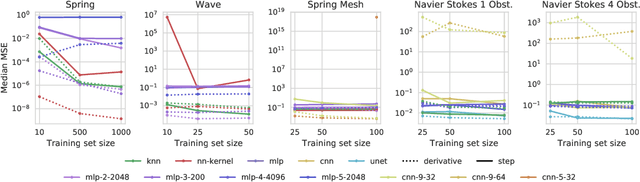
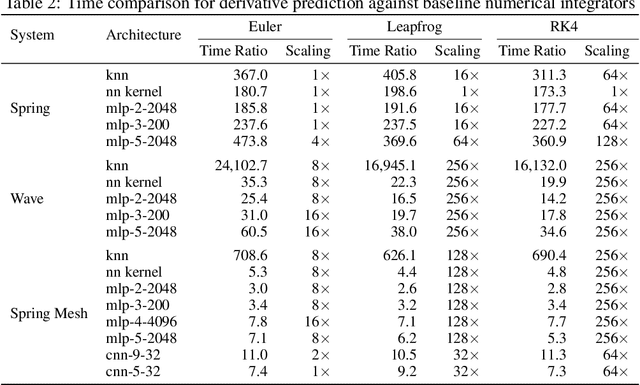
Simulating physical systems is a core component of scientific computing, encompassing a wide range of physical domains and applications. Recently, there has been a surge in data-driven methods to complement traditional numerical simulations methods, motivated by the opportunity to reduce computational costs and/or learn new physical models leveraging access to large collections of data. However, the diversity of problem settings and applications has led to a plethora of approaches, each one evaluated on a different setup and with different evaluation metrics. We introduce a set of benchmark problems to take a step towards unified benchmarks and evaluation protocols. We propose four representative physical systems, as well as a collection of both widely used classical time integrators and representative data-driven methods (kernel-based, MLP, CNN, nearest neighbors). Our framework allows evaluating objectively and systematically the stability, accuracy, and computational efficiency of data-driven methods. Additionally, it is configurable to permit adjustments for accommodating other learning tasks and for establishing a foundation for future developments in machine learning for scientific computing.

Orienting Point Clouds with Dipole Propagation

Establishing a consistent normal orientation for point clouds is a notoriously difficult problem in geometry processing, requiring attention to both local and global shape characteristics. The normal direction of a point is a function of the local surface neighborhood; yet, point clouds do not disclose the full underlying surface structure. Even assuming known geodesic proximity, calculating a consistent normal orientation requires the global context. In this work, we introduce a novel approach for establishing a globally consistent normal orientation for point clouds. Our solution separates the local and global components into two different sub-problems. In the local phase, we train a neural network to learn a coherent normal direction per patch (i.e., consistently oriented normals within a single patch). In the global phase, we propagate the orientation across all coherent patches using a dipole propagation. Our dipole propagation decides to orient each patch using the electric field defined by all previously orientated patches. This gives rise to a global propagation that is stable, as well as being robust to nearby surfaces, holes, sharp features and noise.

DEF: Deep Estimation of Sharp Geometric Features in 3D Shapes

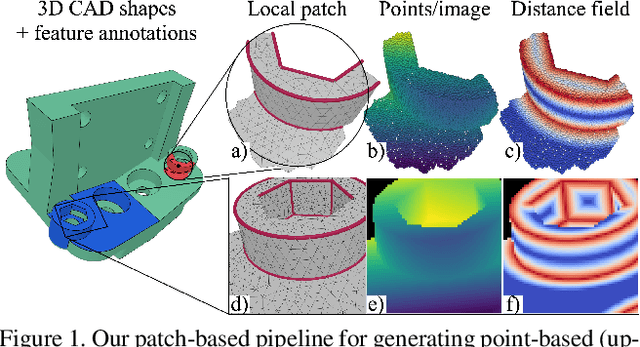
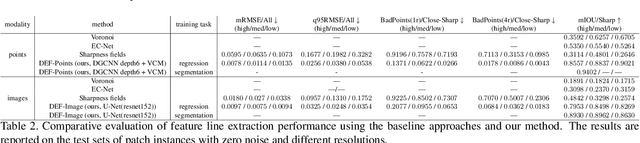
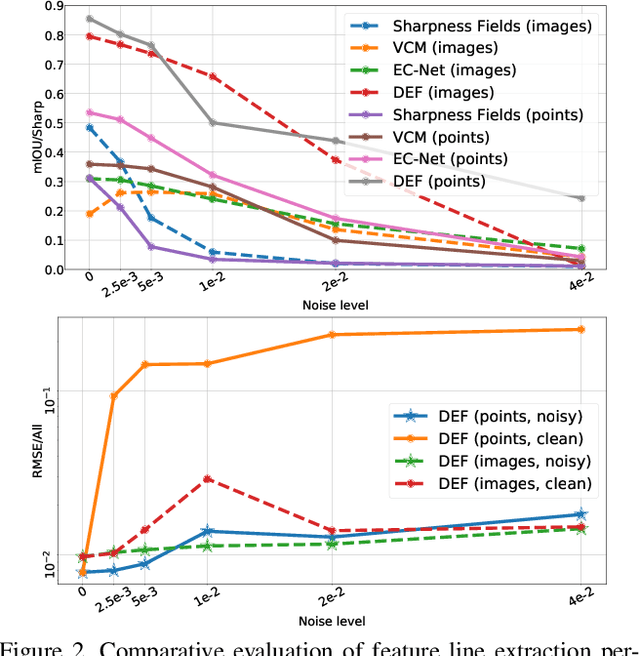
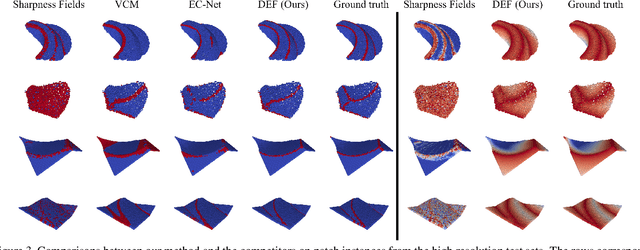
Sharp feature lines carry essential information about human-made objects, enabling compact 3D shape representations, high-quality surface reconstruction, and are a signal source for mesh processing. While extracting high-quality lines from noisy and undersampled data is challenging for traditional methods, deep learning-powered algorithms can leverage global and semantic information from the training data to aid in the process. We propose Deep Estimators of Features (DEFs), a learning-based framework for predicting sharp geometric features in sampled 3D shapes. Differently from existing data-driven methods, which reduce this problem to feature classification, we propose to regress a scalar field representing the distance from point samples to the closest feature line on local patches. By fusing the result of individual patches, we can process large 3D models, which are impossible to process for existing data-driven methods due to their size and complexity. Extensive experimental evaluation of DEFs is implemented on synthetic and real-world 3D shape datasets and suggests advantages of our image- and point-based estimators over competitor methods, as well as improved noise robustness and scalability of our approach.

Robust & Asymptotically Locally Optimal UAV-Trajectory Generation Based on Spline Subdivision

Generating locally optimal UAV-trajectories is challenging due to the non-convex constraints of collision avoidance and actuation limits. We present the first local, optimization-based UAV-trajectory generator that simultaneously guarantees validity and asymptotic optimality. Validity: Given a feasible initial guess, our algorithm guarantees the satisfaction of all constraints throughout the process of optimization. Asymptotic Optimality: We use a conservative piecewise approximation of the trajectory with automatically adjustable resolution of its discretization. The trajectory converges under refinement to the first-order stationary point of the exact non-convex programming problem. Our method has additional practical advantages including joint optimality in terms of trajectory and time-allocation, and robustness to challenging environments as demonstrated in our experiments.

VoronoiNet: General Functional Approximators with Local Support

Voronoi diagrams are highly compact representations that are used in various Graphics applications. In this work, we show how to embed a differentiable version of it -- via a novel deep architecture -- into a generative deep network. By doing so, we achieve a highly compact latent embedding that is able to provide much more detailed reconstructions, both in 2D and 3D, for various shapes. In this tech report, we introduce our representation and present a set of preliminary results comparing it with recently proposed implicit occupancy networks.

Gradient Dynamics of Shallow Univariate ReLU Networks

We present a theoretical and empirical study of the gradient dynamics of overparameterized shallow ReLU networks with one-dimensional input, solving least-squares interpolation. We show that the gradient dynamics of such networks are determined by the gradient flow in a non-redundant parameterization of the network function. We examine the principal qualitative features of this gradient flow. In particular, we determine conditions for two learning regimes:kernel and adaptive, which depend both on the relative magnitude of initialization of weights in different layers and the asymptotic behavior of initialization coefficients in the limit of large network widths. We show that learning in the kernel regime yields smooth interpolants, minimizing curvature, and reduces to cubic splines for uniform initializations. Learning in the adaptive regime favors instead linear splines, where knots cluster adaptively at the sample points.

ABC: A Big CAD Model Dataset For Geometric Deep Learning

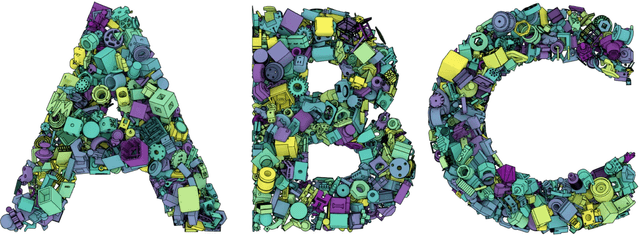
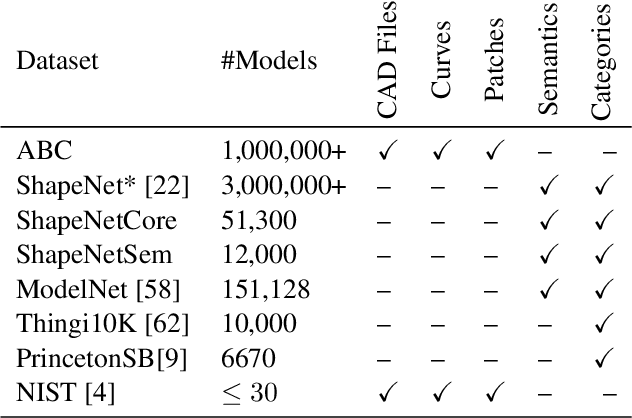
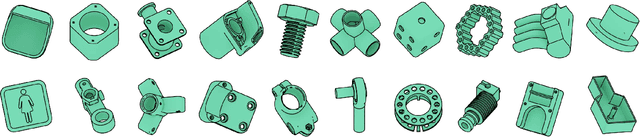
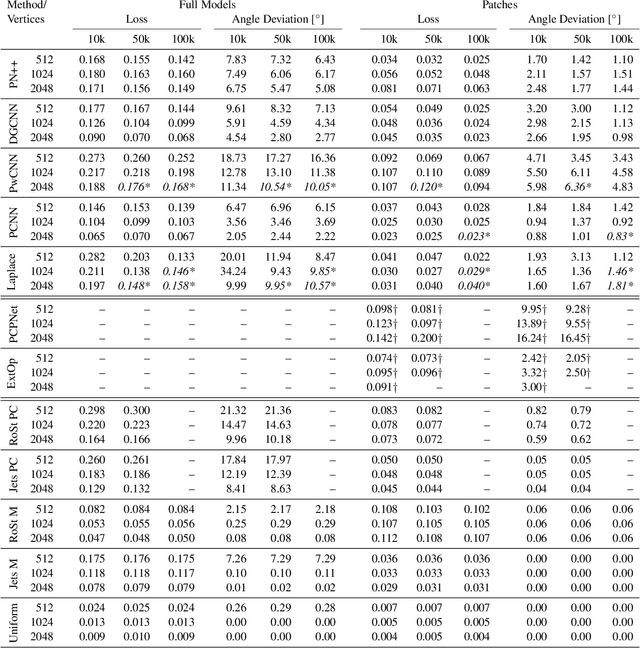
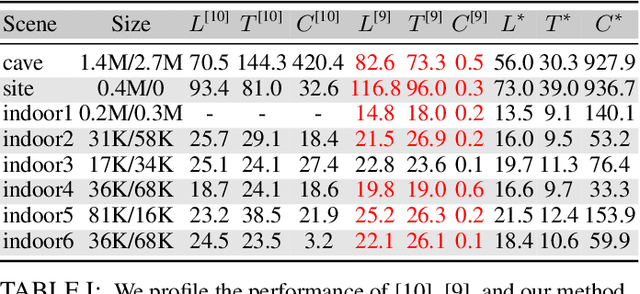
We introduce ABC-Dataset, a collection of one million Computer-Aided Design (CAD) models for research of geometric deep learning methods and applications. Each model is a collection of explicitly parametrized curves and surfaces, providing ground truth for differential quantities, patch segmentation, geometric feature detection, and shape reconstruction. Sampling the parametric descriptions of surfaces and curves allows generating data in different formats and resolutions, enabling fair comparisons for a wide range of geometric learning algorithms. As a use case for our dataset, we perform a large-scale benchmark for estimation of surface normals, comparing existing data driven methods and evaluating their performance against both the ground truth and traditional normal estimation methods.

Deep Geometric Prior for Surface Reconstruction

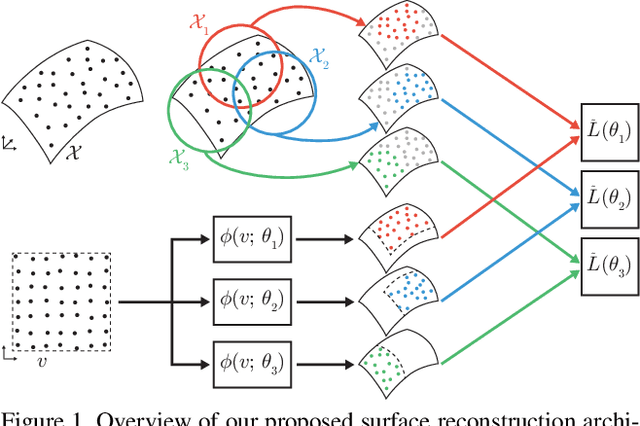
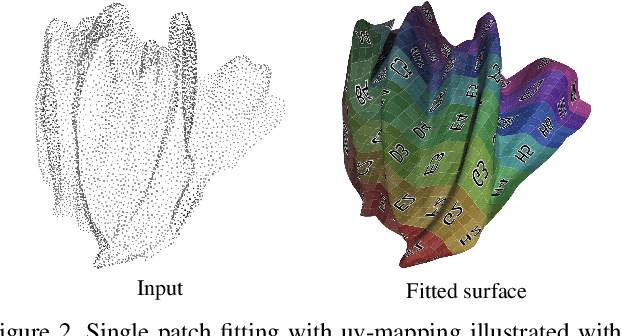
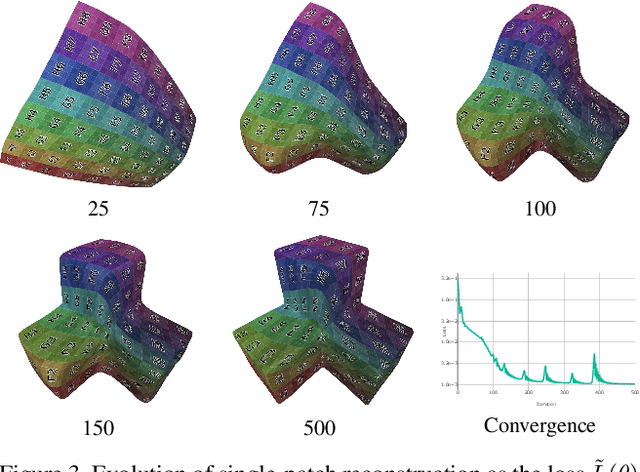
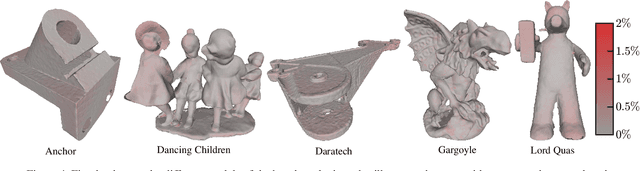
The reconstruction of a discrete surface from a point cloud is a fundamental geometry processing problem that has been studied for decades, with many methods developed. We propose the use of a deep neural network as a geometric prior for surface reconstruction. Specifically, we overfit a neural network representing a local chart parameterization to part of an input point cloud using the Wasserstein distance as a measure of approximation. By jointly fitting many such networks to overlapping parts of the point cloud, while enforcing a consistency condition, we compute a manifold atlas. By sampling this atlas, we can produce a dense reconstruction of the surface approximating the input cloud. The entire procedure does not require any training data or explicit regularization, yet, we show that it is able to perform remarkably well: not introducing typical overfitting artifacts, and approximating sharp features closely at the same time. We experimentally show that this geometric prior produces good results for both man-made objects containing sharp features and smoother organic objects, as well as noisy inputs. We compare our method with a number of well-known reconstruction methods on a standard surface reconstruction benchmark.