SDRS: Shape-Differentiable Robot Simulator

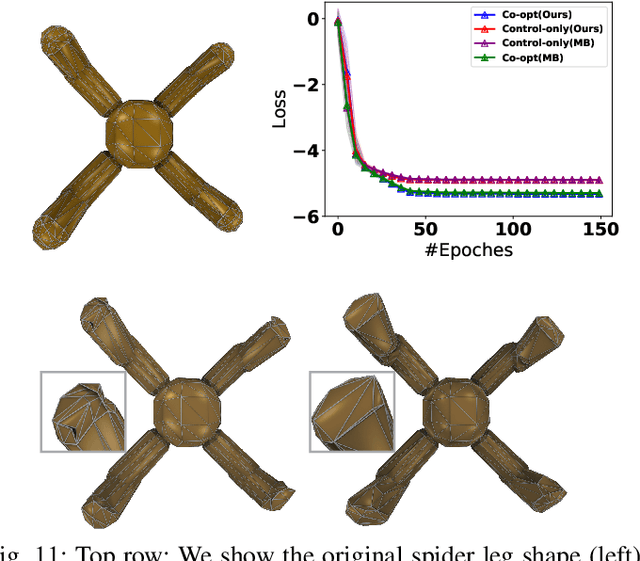
Robot simulators are indispensable tools across many fields, and recent research has significantly improved their functionality by incorporating additional gradient information. However, existing differentiable robot simulators suffer from non-differentiable singularities, when robots undergo substantial shape changes. To address this, we present the Shape-Differentiable Robot Simulator (SDRS), designed to be differentiable under significant robot shape changes. The core innovation of SDRS lies in its representation of robot shapes using a set of convex polyhedrons. This approach allows us to generalize smooth, penalty-based contact mechanics for interactions between any pair of convex polyhedrons. Using the separating hyperplane theorem, SDRS introduces a separating plane for each pair of contacting convex polyhedrons. This separating plane functions as a zero-mass auxiliary entity, with its state determined by the principle of least action. This setup ensures global differentiability, even as robot shapes undergo significant geometric and topological changes. To demonstrate the practical value of SDRS, we provide examples of robot co-design scenarios, where both robot shapes and control movements are optimized simultaneously.

Learning Neural Traffic Rules

Extensive research has been devoted to the field of multi-agent navigation. Recently, there has been remarkable progress attributed to the emergence of learning-based techniques with substantially elevated intelligence and realism. Nonetheless, prevailing learned models face limitations in terms of scalability and effectiveness, primarily due to their agent-centric nature, i.e., the learned neural policy is individually deployed on each agent. Inspired by the efficiency observed in real-world traffic networks, we present an environment-centric navigation policy. Our method learns a set of traffic rules to coordinate a vast group of unintelligent agents that possess only basic collision-avoidance capabilities. Our method segments the environment into distinct blocks and parameterizes the traffic rule using a Graph Recurrent Neural Network (GRNN) over the block network. Each GRNN node is trained to modulate the velocities of agents as they traverse through. Using either Imitation Learning (IL) or Reinforcement Learning (RL) schemes, we demonstrate the efficacy of our neural traffic rules in resolving agent congestion, closely resembling real-world traffic regulations. Our method handles up to $240$ agents at real-time and generalizes across diverse agent and environment configurations.

Consistent Mesh Diffusion

Given a 3D mesh with a UV parameterization, we introduce a novel approach to generating textures from text prompts. While prior work uses optimization from Text-to-Image Diffusion models to generate textures and geometry, this is slow and requires significant compute resources. Alternatively, there are projection based approaches that use the same Text-to-Image models that paint images onto a mesh, but lack consistency at different viewing angles, we propose a method that uses a single Depth-to-Image diffusion network, and generates a single consistent texture when rendered on the 3D surface by first unifying multiple 2D image's diffusion paths, and hoisting that to 3D with MultiDiffusion~\cite{multidiffusion}. We demonstrate our approach on a dataset containing 30 meshes, taking approximately 5 minutes per mesh. To evaluate the quality of our approach, we use CLIP-score~\cite{clipscore} and Frechet Inception Distance (FID)~\cite{frechet} to evaluate the quality of the rendering, and show our improvement over prior work.

GaussianShader: 3D Gaussian Splatting with Shading Functions for Reflective Surfaces

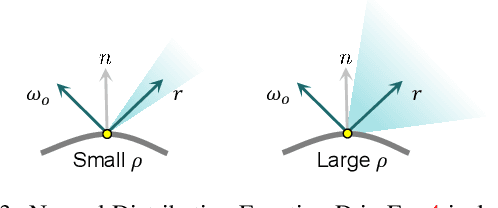
The advent of neural 3D Gaussians has recently brought about a revolution in the field of neural rendering, facilitating the generation of high-quality renderings at real-time speeds. However, the explicit and discrete representation encounters challenges when applied to scenes featuring reflective surfaces. In this paper, we present GaussianShader, a novel method that applies a simplified shading function on 3D Gaussians to enhance the neural rendering in scenes with reflective surfaces while preserving the training and rendering efficiency. The main challenge in applying the shading function lies in the accurate normal estimation on discrete 3D Gaussians. Specifically, we proposed a novel normal estimation framework based on the shortest axis directions of 3D Gaussians with a delicately designed loss to make the consistency between the normals and the geometries of Gaussian spheres. Experiments show that GaussianShader strikes a commendable balance between efficiency and visual quality. Our method surpasses Gaussian Splatting in PSNR on specular object datasets, exhibiting an improvement of 1.57dB. When compared to prior works handling reflective surfaces, such as Ref-NeRF, our optimization time is significantly accelerated (23h vs. 0.58h). Please click on our project website to see more results.

Second-Order Convergent Collision-Constrained Optimization-Based Planner

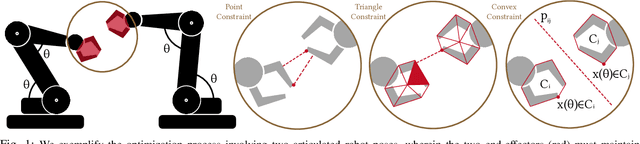
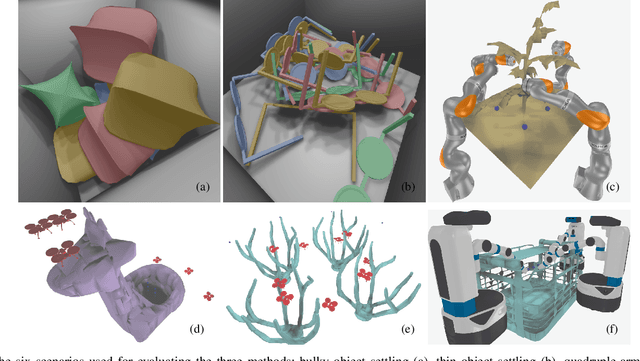
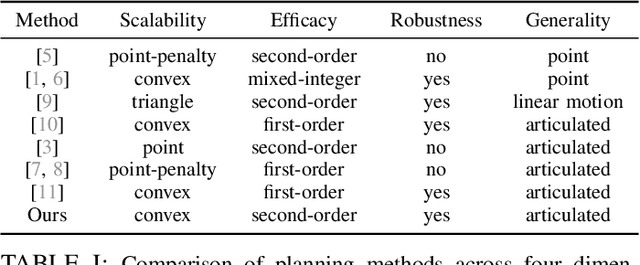
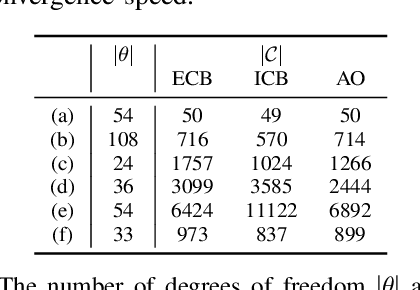
Finding robot poses and trajectories represents a foundational aspect of robot motion planning. Despite decades of research, efficiently and robustly addressing these challenges is still difficult. Existing approaches are often plagued by various limitations, such as intricate geometric approximations, violations of collision constraints, or slow first-order convergence. In this paper, we introduce two novel optimization formulations that offer provable robustness, achieving second-order convergence while requiring only a convex approximation of the robot's links and obstacles. Our first method, known as the Explicit Collision Barrier (ECB) method, employs a barrier function to guarantee separation between convex objects. ECB uses an efficient matrix factorization technique, enabling a second-order Newton's method with an iterative complexity linear in the number of separating planes. Our second method, referred to as the Implicit Collision Barrier (ICB) method, further transforms the separating planes into implicit functions of robot poses. We show such an implicit objective function is twice-differentiable, with derivatives evaluated at a linear complexity. To assess the effectiveness of our approaches, we conduct a comparative study with a first-order baseline algorithm across six testing scenarios. Our results unequivocally justify that our method exhibits significantly faster convergence rates compared to the baseline algorithm.

Learning Reduced-Order Soft Robot Controller

Deformable robots are notoriously difficult to model or control due to its high-dimensional configuration spaces. Direct trajectory optimization suffers from the curse-of-dimensionality and incurs a high computational cost, while learning-based controller optimization methods are sensitive to hyper-parameter tuning. To overcome these limitations, we hypothesize that high fidelity soft robots can be both simulated and controlled by restricting to low-dimensional spaces. Under such assumption, we propose a two-stage algorithm to identify such simulation- and control-spaces. Our method first identifies the so-called simulation-space that captures the salient deformation modes, to which the robot's governing equation is restricted. We then identify the control-space, to which control signals are restricted. We propose a multi-fidelity Riemannian Bayesian bilevel optimization to identify task-specific control spaces. We show that the dimension of control-space can be less than $10$ for a high-DOF soft robot to accomplish walking and swimming tasks, allowing low-dimensional MPC controllers to be applied to soft robots with tractable computational complexity.

Learning based 2D Irregular Shape Packing

2D irregular shape packing is a necessary step to arrange UV patches of a 3D model within a texture atlas for memory-efficient appearance rendering in computer graphics. Being a joint, combinatorial decision-making problem involving all patch positions and orientations, this problem has well-known NP-hard complexity. Prior solutions either assume a heuristic packing order or modify the upstream mesh cut and UV mapping to simplify the problem, which either limits the packing ratio or incurs robustness or generality issues. Instead, we introduce a learning-assisted 2D irregular shape packing method that achieves a high packing quality with minimal requirements from the input. Our method iteratively selects and groups subsets of UV patches into near-rectangular super patches, essentially reducing the problem to bin-packing, based on which a joint optimization is employed to further improve the packing ratio. In order to efficiently deal with large problem instances with hundreds of patches, we train deep neural policies to predict nearly rectangular patch subsets and determine their relative poses, leading to linear time scaling with the number of patches. We demonstrate the effectiveness of our method on three datasets for UV packing, where our method achieves a higher packing ratio over several widely used baselines with competitive computational speed.

Provably Robust Semi-Infinite Program Under Collision Constraints via Subdivision

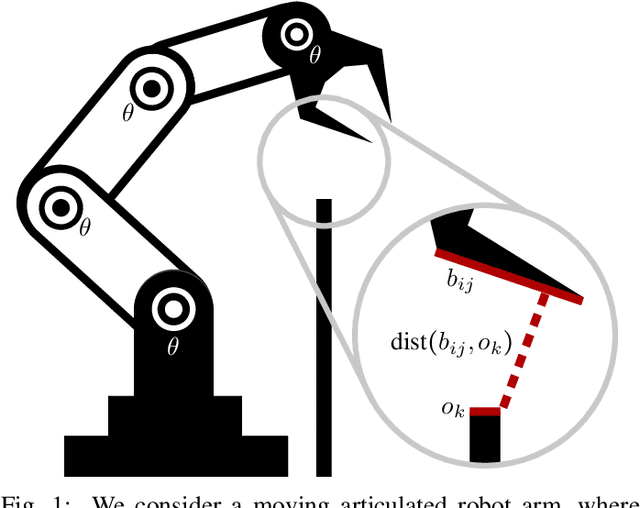
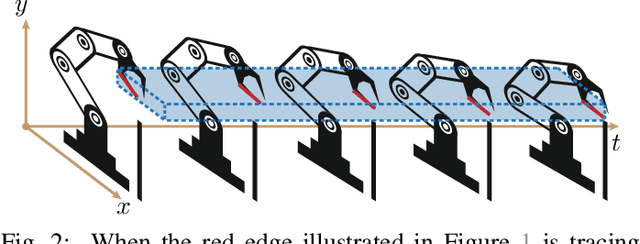
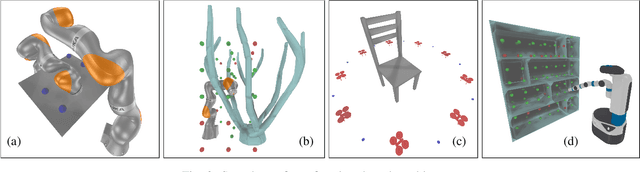
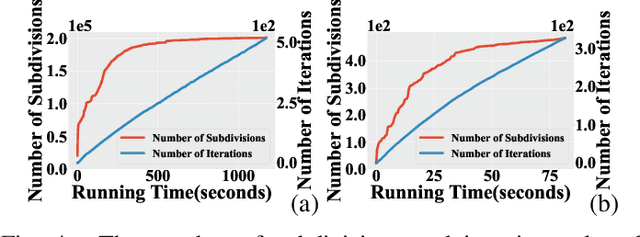
We present a semi-infinite program (SIP) solver for trajectory optimizations of general articulated robots. These problems are more challenging than standard Nonlinear Program (NLP) by involving an infinite number of non-convex, collision constraints. Prior SIP solvers based on constraint sampling cannot guarantee the satisfaction of all constraints. Instead, our method uses a conservative bound on articulated body motions to ensure the solution feasibility throughout the optimization procedure. We further use subdivision to adaptively reduce the error in conservative motion estimation. Combined, we prove that our SIP solver guarantees feasibility while approaches the critical point of SIP problems up to arbitrary user-provided precision. We have verified our method on a row of trajectory optimization problems involving industrial robot arms and UAVs, where our method can generate collision-free, locally optimal trajectories within a couple minutes.

First-Order Bilevel Topology Optimization for Fast Mechanical Design

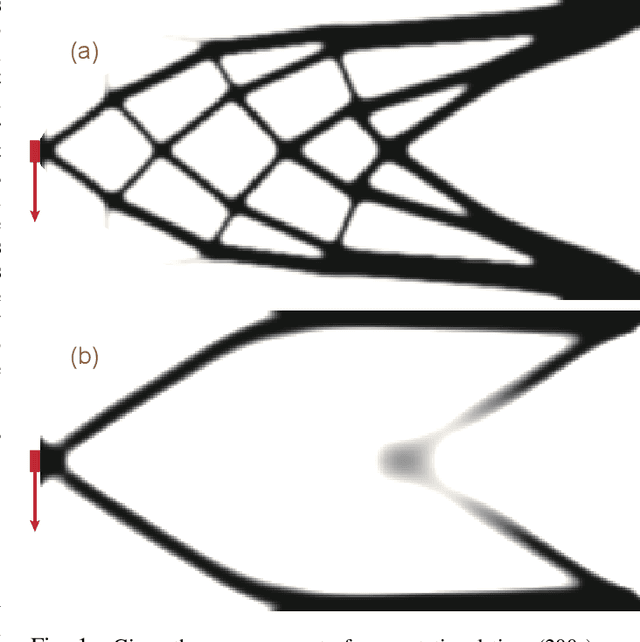
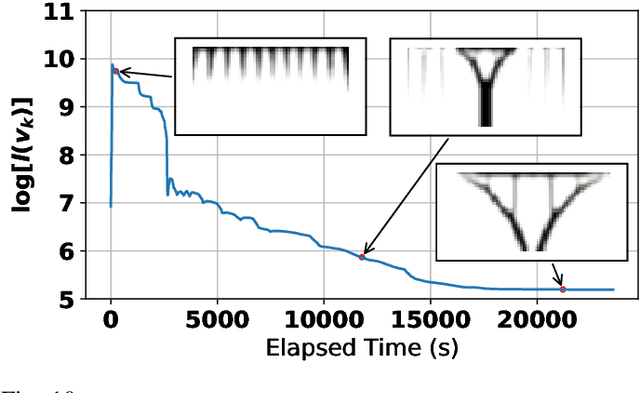
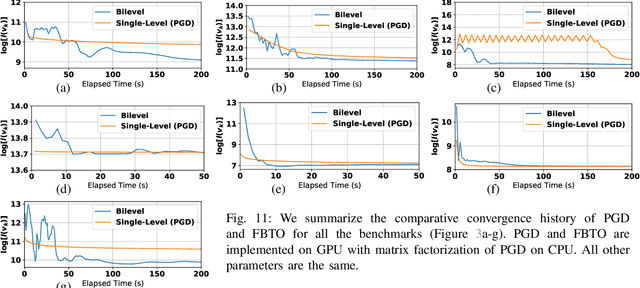
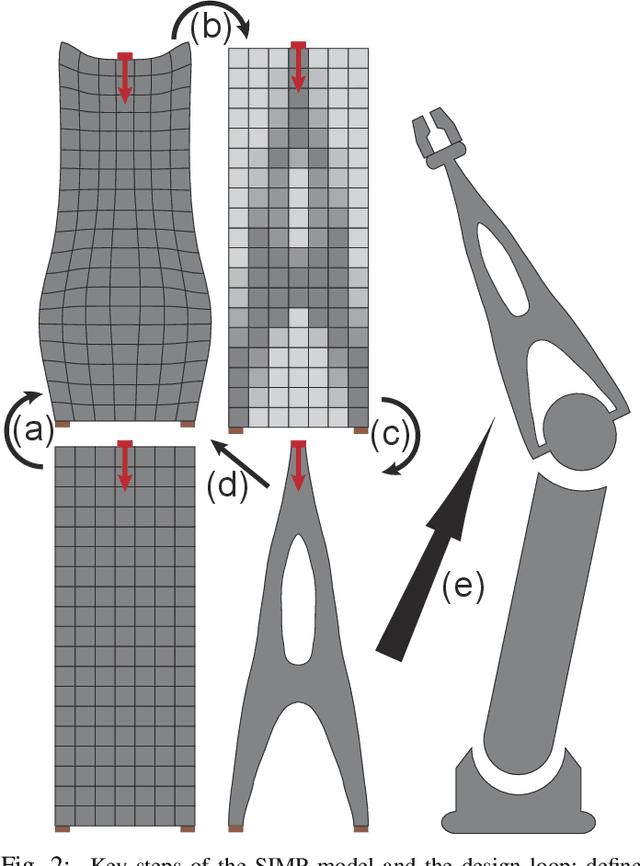
Topology Optimization (TO), which maximizes structural robustness under material weight constraints, is becoming an essential step for the automatic design of mechanical parts. However, existing TO algorithms use the Finite Element Analysis (FEA) that requires massive computational resources. We present a novel TO algorithm that incurs a much lower iterative cost. Unlike conventional methods that require exact inversions of large FEA system matrices at every iteration, we reformulate the problem as a bilevel optimization that can be solved using a first-order algorithm and only inverts the system matrix approximately. As a result, our method incurs a low iterative cost, and users can preview the TO results interactively for fast design updates. Theoretical convergence analysis and numerical experiments are conducted to verify our effectiveness. We further discuss extensions to use high-performance preconditioners and fine-grained parallelism on the Graphics Processing Unit (GPU).

Robust Multi-Robot Trajectory Generation Using Alternating Direction Method of Multiplier

We propose a variant of alternating direction method of multiplier (ADMM) to solve constrained trajectory optimization problems. Our ADMM framework breaks a joint optimization into small sub-problems, leading to a low iteration cost and decentralized parameter updates. Our method inherits the theoretical properties of primal interior point method (P-IPM), i.e., guaranteed collision avoidance and homotopy preservation, while being orders of magnitude faster. We have analyzed the convergence and evaluated our method for time-optimal multi-UAV trajectory optimizations and simultaneous goal-reaching of multiple robot arms, where we take into consider kinematics-, dynamics-limits, and homotopy-preserving collision constraints. Our method highlights 10-100 times speedup, while generating trajectories of comparable qualities as state-of-the-art P-IPM solver.