Provably Robust Semi-Infinite Program Under Collision Constraints via Subdivision
Paper and Code
Feb 02, 2023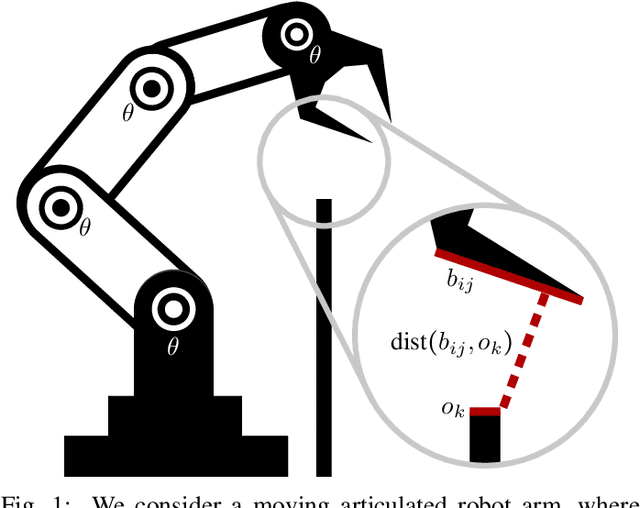
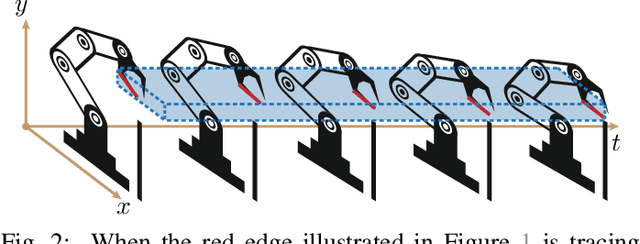
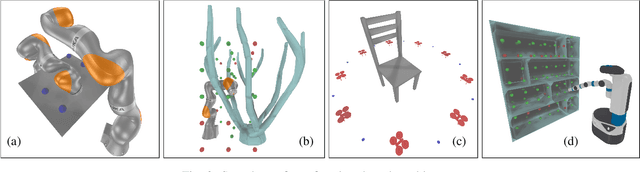
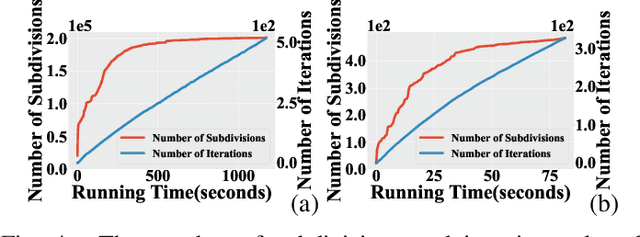
We present a semi-infinite program (SIP) solver for trajectory optimizations of general articulated robots. These problems are more challenging than standard Nonlinear Program (NLP) by involving an infinite number of non-convex, collision constraints. Prior SIP solvers based on constraint sampling cannot guarantee the satisfaction of all constraints. Instead, our method uses a conservative bound on articulated body motions to ensure the solution feasibility throughout the optimization procedure. We further use subdivision to adaptively reduce the error in conservative motion estimation. Combined, we prove that our SIP solver guarantees feasibility while approaches the critical point of SIP problems up to arbitrary user-provided precision. We have verified our method on a row of trajectory optimization problems involving industrial robot arms and UAVs, where our method can generate collision-free, locally optimal trajectories within a couple minutes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge