Second-Order Convergent Collision-Constrained Optimization-Based Planner
Paper and Code
Nov 03, 2023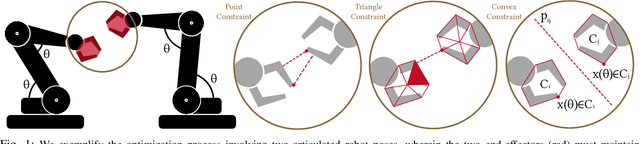
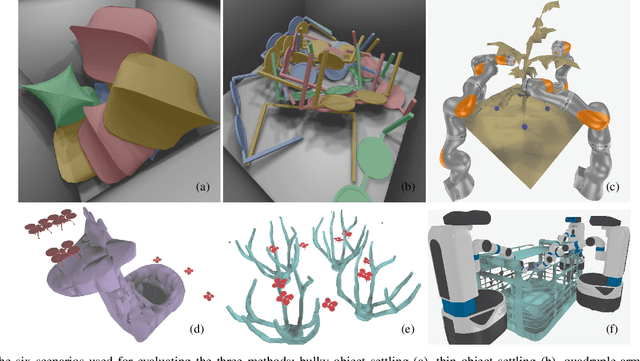
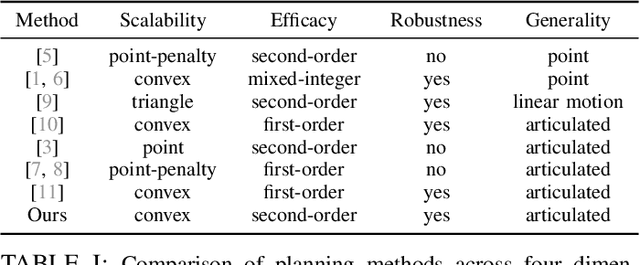
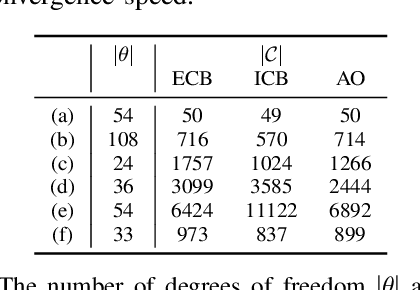
Finding robot poses and trajectories represents a foundational aspect of robot motion planning. Despite decades of research, efficiently and robustly addressing these challenges is still difficult. Existing approaches are often plagued by various limitations, such as intricate geometric approximations, violations of collision constraints, or slow first-order convergence. In this paper, we introduce two novel optimization formulations that offer provable robustness, achieving second-order convergence while requiring only a convex approximation of the robot's links and obstacles. Our first method, known as the Explicit Collision Barrier (ECB) method, employs a barrier function to guarantee separation between convex objects. ECB uses an efficient matrix factorization technique, enabling a second-order Newton's method with an iterative complexity linear in the number of separating planes. Our second method, referred to as the Implicit Collision Barrier (ICB) method, further transforms the separating planes into implicit functions of robot poses. We show such an implicit objective function is twice-differentiable, with derivatives evaluated at a linear complexity. To assess the effectiveness of our approaches, we conduct a comparative study with a first-order baseline algorithm across six testing scenarios. Our results unequivocally justify that our method exhibits significantly faster convergence rates compared to the baseline algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge