Physics-informed Neural Mapping and Motion Planning in Unknown Environments

Mapping and motion planning are two essential elements of robot intelligence that are interdependent in generating environment maps and navigating around obstacles. The existing mapping methods create maps that require computationally expensive motion planning tools to find a path solution. In this paper, we propose a new mapping feature called arrival time fields, which is a solution to the Eikonal equation. The arrival time fields can directly guide the robot in navigating the given environments. Therefore, this paper introduces a new approach called Active Neural Time Fields (Active NTFields), which is a physics-informed neural framework that actively explores the unknown environment and maps its arrival time field on the fly for robot motion planning. Our method does not require any expert data for learning and uses neural networks to directly solve the Eikonal equation for arrival time field mapping and motion planning. We benchmark our approach against state-of-the-art mapping and motion planning methods and demonstrate its superior performance in both simulated and real-world environments with a differential drive robot and a 6 degrees-of-freedom (DOF) robot manipulator. The supplementary videos can be found at https://youtu.be/qTPL5a6pRKk, and the implementation code repository is available at https://github.com/Rtlyc/antfields-demo.

Physics-informed Neural Motion Planning on Constraint Manifolds

Constrained Motion Planning (CMP) aims to find a collision-free path between the given start and goal configurations on the kinematic constraint manifolds. These problems appear in various scenarios ranging from object manipulation to legged-robot locomotion. However, the zero-volume nature of manifolds makes the CMP problem challenging, and the state-of-the-art methods still take several seconds to find a path and require a computationally expansive path dataset for imitation learning. Recently, physics-informed motion planning methods have emerged that directly solve the Eikonal equation through neural networks for motion planning and do not require expert demonstrations for learning. Inspired by these approaches, we propose the first physics-informed CMP framework that solves the Eikonal equation on the constraint manifolds and trains neural function for CMP without expert data. Our results show that the proposed approach efficiently solves various CMP problems in both simulation and real-world, including object manipulation under orientation constraints and door opening with a high-dimensional 6-DOF robot manipulator. In these complex settings, our method exhibits high success rates and finds paths in sub-seconds, which is many times faster than the state-of-the-art CMP methods.

Progressive Learning for Physics-informed Neural Motion Planning

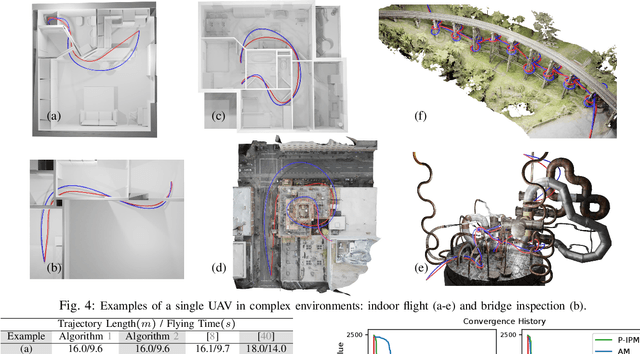
Motion planning (MP) is one of the core robotics problems requiring fast methods for finding a collision-free robot motion path connecting the given start and goal states. Neural motion planners (NMPs) demonstrate fast computational speed in finding path solutions but require a huge amount of expert trajectories for learning, thus adding a significant training computational load. In contrast, recent advancements have also led to a physics-informed NMP approach that directly solves the Eikonal equation for motion planning and does not require expert demonstrations for learning. However, experiments show that the physics-informed NMP approach performs poorly in complex environments and lacks scalability in multiple scenarios and high-dimensional real robot settings. To overcome these limitations, this paper presents a novel and tractable Eikonal equation formulation and introduces a new progressive learning strategy to train neural networks without expert data in complex, cluttered, multiple high-dimensional robot motion planning scenarios. The results demonstrate that our method outperforms state-of-the-art traditional MP, data-driven NMP, and physics-informed NMP methods by a significant margin in terms of computational planning speed, path quality, and success rates. We also show that our approach scales to multiple complex, cluttered scenarios and the real robot set up in a narrow passage environment. The proposed method's videos and code implementations are available at https://github.com/ruiqini/P-NTFields.

NTFields: Neural Time Fields for Physics-Informed Robot Motion Planning

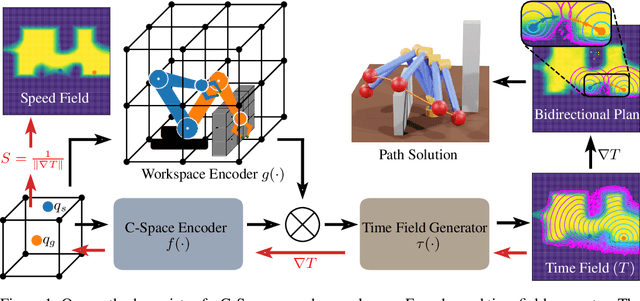
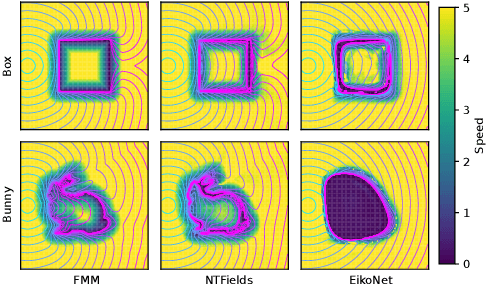
Neural Motion Planners (NMPs) have emerged as a promising tool for solving robot navigation tasks in complex environments. However, these methods often require expert data for learning, which limits their application to scenarios where data generation is time-consuming. Recent developments have also led to physics-informed deep neural models capable of representing complex dynamical Partial Differential Equations (PDEs). Inspired by these developments, we propose Neural Time Fields (NTFields) for robot motion planning in cluttered scenarios. Our framework represents a wave propagation model generating continuous arrival time to find path solutions informed by a nonlinear first-order PDE called Eikonal Equation. We evaluate our method in various cluttered 3D environments, including the Gibson dataset, and demonstrate its ability to solve motion planning problems for 4-DOF and 6-DOF robot manipulators where the traditional grid-based Eikonal planners often face the curse of dimensionality. Furthermore, the results show that our method exhibits high success rates and significantly lower computational times than the state-of-the-art methods, including NMPs that require training data from classical planners.

Robust Multi-Robot Trajectory Generation Using Alternating Direction Method of Multiplier

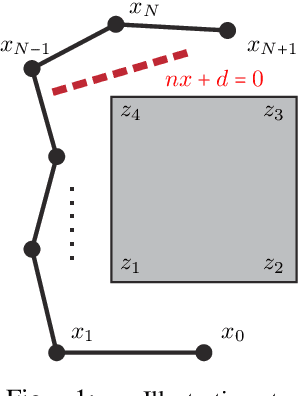
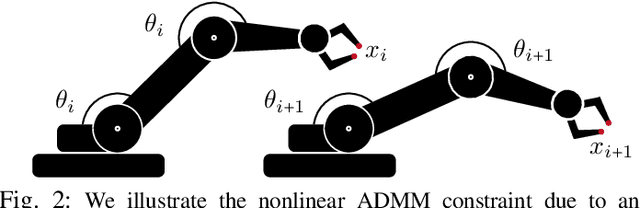
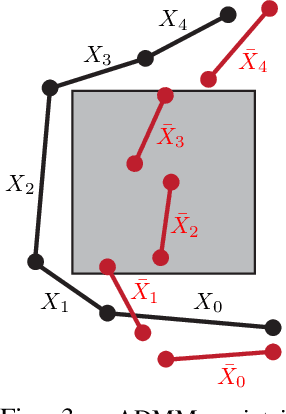
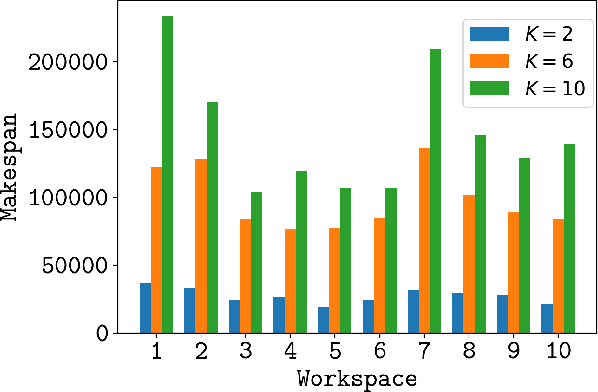
We propose a variant of alternating direction method of multiplier (ADMM) to solve constrained trajectory optimization problems. Our ADMM framework breaks a joint optimization into small sub-problems, leading to a low iteration cost and decentralized parameter updates. Our method inherits the theoretical properties of primal interior point method (P-IPM), i.e., guaranteed collision avoidance and homotopy preservation, while being orders of magnitude faster. We have analyzed the convergence and evaluated our method for time-optimal multi-UAV trajectory optimizations and simultaneous goal-reaching of multiple robot arms, where we take into consider kinematics-, dynamics-limits, and homotopy-preserving collision constraints. Our method highlights 10-100 times speedup, while generating trajectories of comparable qualities as state-of-the-art P-IPM solver.

Multi-Robot Path Planning in Complex Environments via Graph Embedding

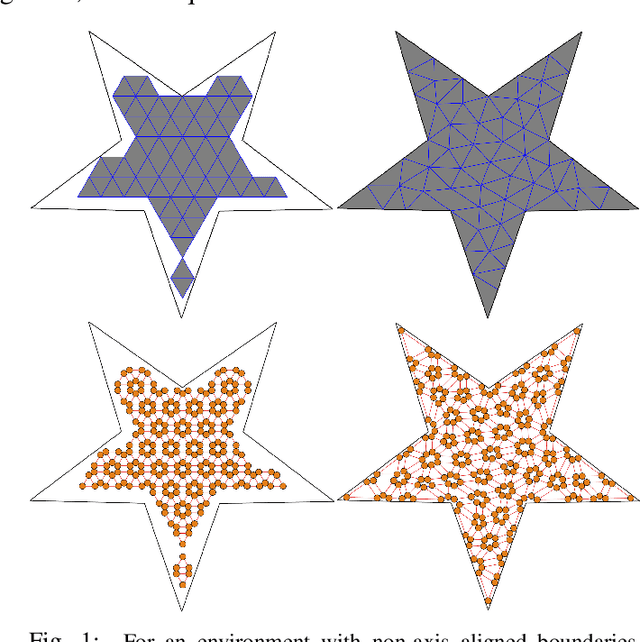
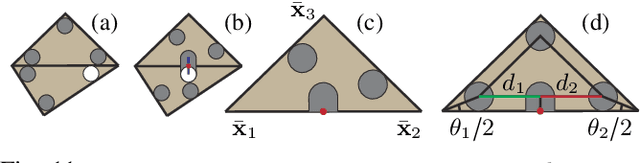
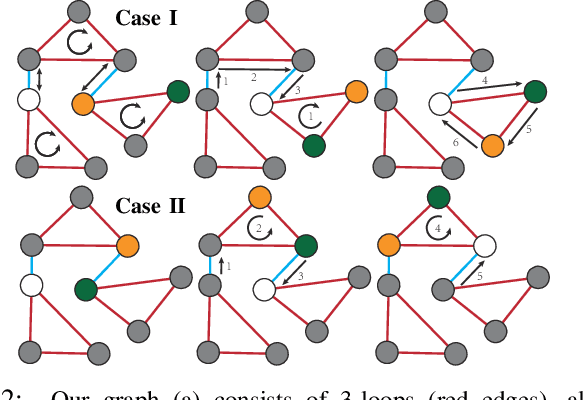
We propose an approach to solve multi-agent path planning (MPP) problems for complex environments. Our method first designs a special pebble graph with a set of feasibility constraints, under which MPP problems have feasibility guarantee. We further propose an algorithm to greedily improve the optimality of planned MPP solutions via parallel pebble motions. As a second step, we develop a mesh optimization algorithm to embed our pebble graph into arbitrarily complex environments. We show that the feasibility constraints of a pebble graph can be converted into differentiable geometric constraints, such that our mesh optimizer can satisfy these constraints via constrained numerical optimization. We have evaluated the effectiveness and efficiency of our method using a set of environments with complex geometries, on which our method achieves an average of 99.0% free-space coverage and 30.3% robot density within hours of computation on a desktop machine.

Robust & Asymptotically Locally Optimal UAV-Trajectory Generation Based on Spline Subdivision

Generating locally optimal UAV-trajectories is challenging due to the non-convex constraints of collision avoidance and actuation limits. We present the first local, optimization-based UAV-trajectory generator that simultaneously guarantees validity and asymptotic optimality. Validity: Given a feasible initial guess, our algorithm guarantees the satisfaction of all constraints throughout the process of optimization. Asymptotic Optimality: We use a conservative piecewise approximation of the trajectory with automatically adjustable resolution of its discretization. The trajectory converges under refinement to the first-order stationary point of the exact non-convex programming problem. Our method has additional practical advantages including joint optimality in terms of trajectory and time-allocation, and robustness to challenging environments as demonstrated in our experiments.