NTFields: Neural Time Fields for Physics-Informed Robot Motion Planning
Paper and Code
Sep 30, 2022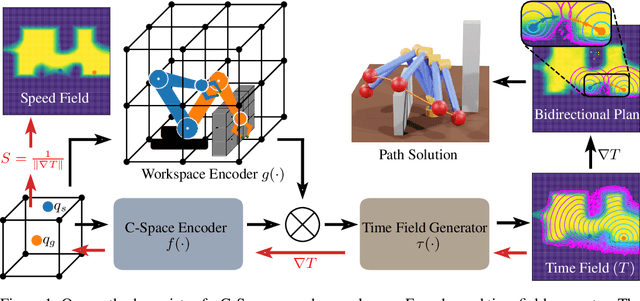

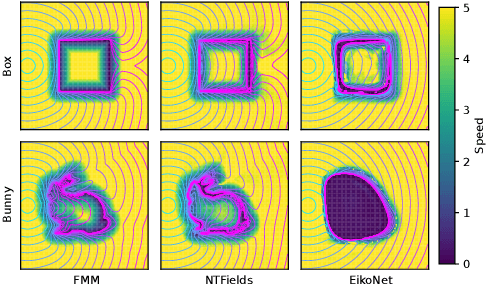

Neural Motion Planners (NMPs) have emerged as a promising tool for solving robot navigation tasks in complex environments. However, these methods often require expert data for learning, which limits their application to scenarios where data generation is time-consuming. Recent developments have also led to physics-informed deep neural models capable of representing complex dynamical Partial Differential Equations (PDEs). Inspired by these developments, we propose Neural Time Fields (NTFields) for robot motion planning in cluttered scenarios. Our framework represents a wave propagation model generating continuous arrival time to find path solutions informed by a nonlinear first-order PDE called Eikonal Equation. We evaluate our method in various cluttered 3D environments, including the Gibson dataset, and demonstrate its ability to solve motion planning problems for 4-DOF and 6-DOF robot manipulators where the traditional grid-based Eikonal planners often face the curse of dimensionality. Furthermore, the results show that our method exhibits high success rates and significantly lower computational times than the state-of-the-art methods, including NMPs that require training data from classical planners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge