Better STEP, a format and dataset for boundary representation

Boundary representation (B-rep) generated from computer-aided design (CAD) is widely used in industry, with several large datasets available. However, the data in these datasets is represented in STEP format, requiring a CAD kernel to read and process it. This dramatically limits their scope and usage in large learning pipelines, as it constrains the possibility of deploying them on computing clusters due to the high cost of per-node licenses. This paper introduces an alternative format based on the open, cross-platform format HDF5 and a corresponding dataset for STEP files, paired with an open-source library to query and process them. Our Python package also provides standard functionalities such as sampling, normals, and curvature to ease integration in existing pipelines. To demonstrate the effectiveness of our format, we converted the Fusion 360 dataset and the ABC dataset. We developed four standard use cases (normal estimation, denoising, surface reconstruction, and segmentation) to assess the integrity of the data and its compliance with the original STEP files.

Neural Kinematic Bases for Fluids

We propose mesh-free fluid simulations that exploit a kinematic neural basis for velocity fields represented by an MLP. We design a set of losses that ensures that these neural bases satisfy fundamental physical properties such as orthogonality, divergence-free, boundary alignment, and smoothness. Our neural bases can then be used to fit an input sketch of a flow, which will inherit the same fundamental properties from the bases. We then can animate such flow in real-time using standard time integrators. Our neural bases can accommodate different domains and naturally extend to three dimensions.

An Extensible Benchmark Suite for Learning to Simulate Physical Systems

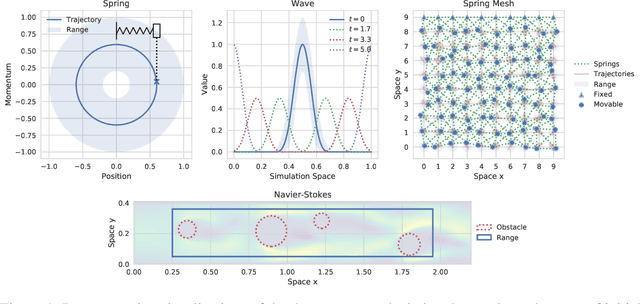
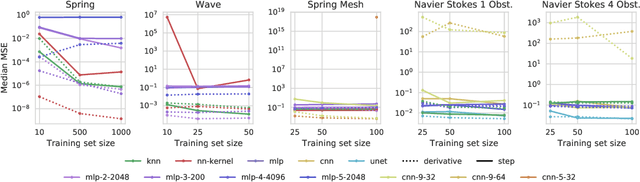
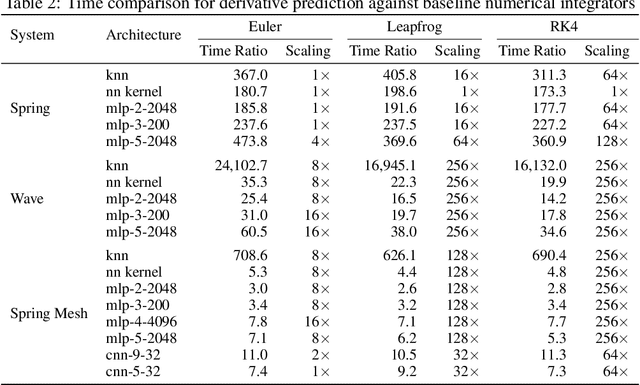
Simulating physical systems is a core component of scientific computing, encompassing a wide range of physical domains and applications. Recently, there has been a surge in data-driven methods to complement traditional numerical simulations methods, motivated by the opportunity to reduce computational costs and/or learn new physical models leveraging access to large collections of data. However, the diversity of problem settings and applications has led to a plethora of approaches, each one evaluated on a different setup and with different evaluation metrics. We introduce a set of benchmark problems to take a step towards unified benchmarks and evaluation protocols. We propose four representative physical systems, as well as a collection of both widely used classical time integrators and representative data-driven methods (kernel-based, MLP, CNN, nearest neighbors). Our framework allows evaluating objectively and systematically the stability, accuracy, and computational efficiency of data-driven methods. Additionally, it is configurable to permit adjustments for accommodating other learning tasks and for establishing a foundation for future developments in machine learning for scientific computing.

Robust & Asymptotically Locally Optimal UAV-Trajectory Generation Based on Spline Subdivision

Generating locally optimal UAV-trajectories is challenging due to the non-convex constraints of collision avoidance and actuation limits. We present the first local, optimization-based UAV-trajectory generator that simultaneously guarantees validity and asymptotic optimality. Validity: Given a feasible initial guess, our algorithm guarantees the satisfaction of all constraints throughout the process of optimization. Asymptotic Optimality: We use a conservative piecewise approximation of the trajectory with automatically adjustable resolution of its discretization. The trajectory converges under refinement to the first-order stationary point of the exact non-convex programming problem. Our method has additional practical advantages including joint optimality in terms of trajectory and time-allocation, and robustness to challenging environments as demonstrated in our experiments.

Deep Geometric Prior for Surface Reconstruction

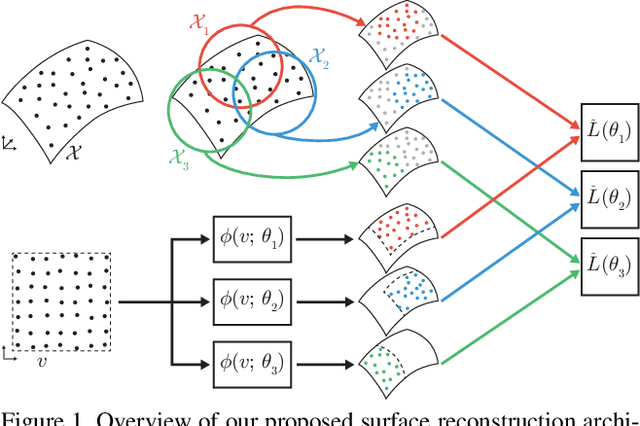
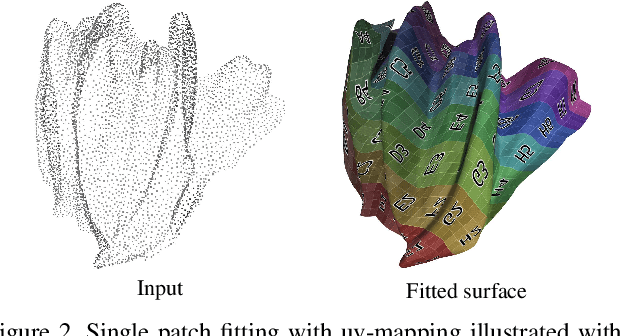
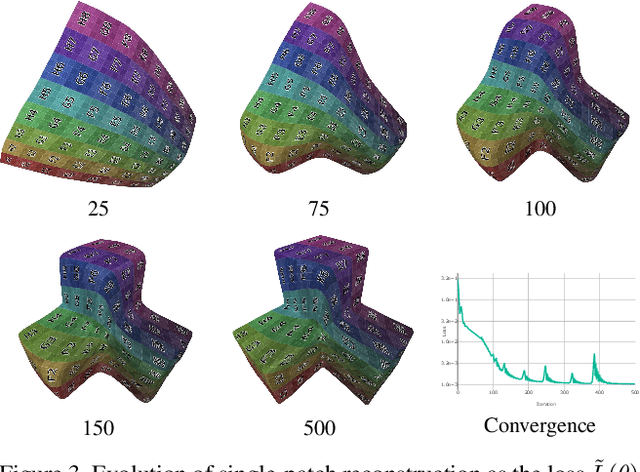
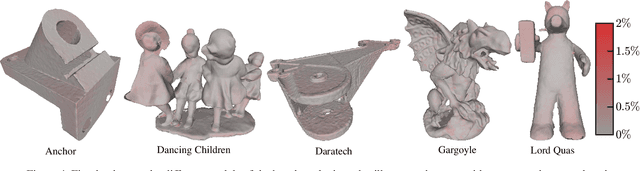
The reconstruction of a discrete surface from a point cloud is a fundamental geometry processing problem that has been studied for decades, with many methods developed. We propose the use of a deep neural network as a geometric prior for surface reconstruction. Specifically, we overfit a neural network representing a local chart parameterization to part of an input point cloud using the Wasserstein distance as a measure of approximation. By jointly fitting many such networks to overlapping parts of the point cloud, while enforcing a consistency condition, we compute a manifold atlas. By sampling this atlas, we can produce a dense reconstruction of the surface approximating the input cloud. The entire procedure does not require any training data or explicit regularization, yet, we show that it is able to perform remarkably well: not introducing typical overfitting artifacts, and approximating sharp features closely at the same time. We experimentally show that this geometric prior produces good results for both man-made objects containing sharp features and smoother organic objects, as well as noisy inputs. We compare our method with a number of well-known reconstruction methods on a standard surface reconstruction benchmark.