Adjoint-based online learning of two-layer quasi-geostrophic baroclinic turbulence

For reasons of computational constraint, most global ocean circulation models used for Earth System Modeling still rely on parameterizations of sub-grid processes, and limitations in these parameterizations affect the modeled ocean circulation and impact on predictive skill. An increasingly popular approach is to leverage machine learning approaches for parameterizations, regressing for a map between the resolved state and missing feedbacks in a fluid system as a supervised learning task. However, the learning is often performed in an `offline' fashion, without involving the underlying fluid dynamical model during the training stage. Here, we explore the `online' approach that involves the fluid dynamical model during the training stage for the learning of baroclinic turbulence and its parameterization, with reference to ocean eddy parameterization. Two online approaches are considered: a full adjoint-based online approach, related to traditional adjoint optimization approaches that require a `differentiable' dynamical model, and an approximately online approach that approximates the adjoint calculation and does not require a differentiable dynamical model. The online approaches are found to be generally more skillful and numerically stable than offline approaches. Others details relating to online training, such as window size, machine learning model set up and designs of the loss functions are detailed to aid in further explorations of the online training methodology for Earth System Modeling.

Data-driven multiscale modeling of subgrid parameterizations in climate models

Subgrid parameterizations, which represent physical processes occurring below the resolution of current climate models, are an important component in producing accurate, long-term predictions for the climate. A variety of approaches have been tested to design these components, including deep learning methods. In this work, we evaluate a proof of concept illustrating a multiscale approach to this prediction problem. We train neural networks to predict subgrid forcing values on a testbed model and examine improvements in prediction accuracy that can be obtained by using additional information in both fine-to-coarse and coarse-to-fine directions.

An Extensible Benchmark Suite for Learning to Simulate Physical Systems

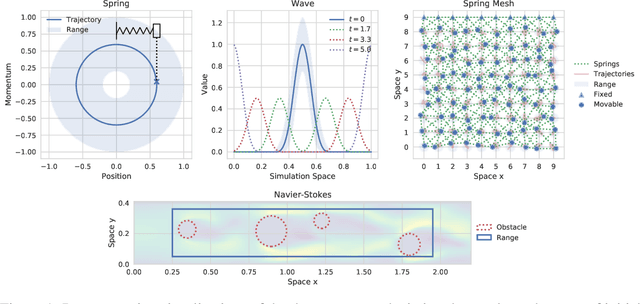
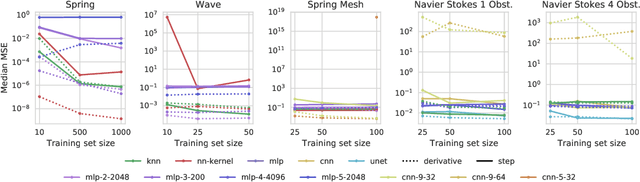
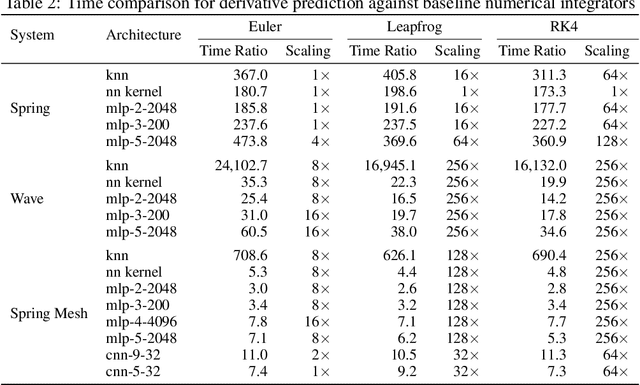
Simulating physical systems is a core component of scientific computing, encompassing a wide range of physical domains and applications. Recently, there has been a surge in data-driven methods to complement traditional numerical simulations methods, motivated by the opportunity to reduce computational costs and/or learn new physical models leveraging access to large collections of data. However, the diversity of problem settings and applications has led to a plethora of approaches, each one evaluated on a different setup and with different evaluation metrics. We introduce a set of benchmark problems to take a step towards unified benchmarks and evaluation protocols. We propose four representative physical systems, as well as a collection of both widely used classical time integrators and representative data-driven methods (kernel-based, MLP, CNN, nearest neighbors). Our framework allows evaluating objectively and systematically the stability, accuracy, and computational efficiency of data-driven methods. Additionally, it is configurable to permit adjustments for accommodating other learning tasks and for establishing a foundation for future developments in machine learning for scientific computing.

MotifNet: a motif-based Graph Convolutional Network for directed graphs

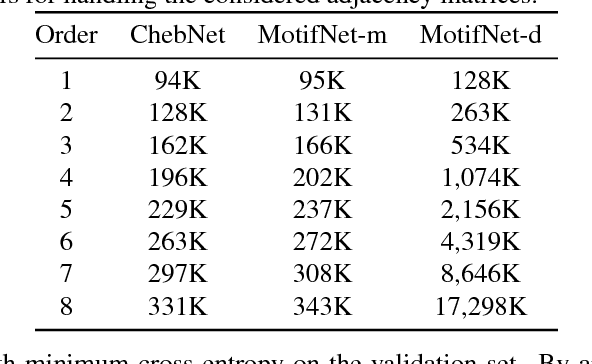
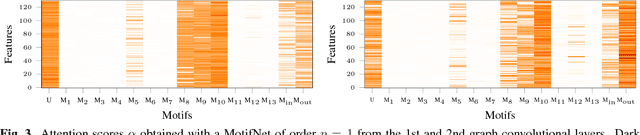
Deep learning on graphs and in particular, graph convolutional neural networks, have recently attracted significant attention in the machine learning community. Many of such techniques explore the analogy between the graph Laplacian eigenvectors and the classical Fourier basis, allowing to formulate the convolution as a multiplication in the spectral domain. One of the key drawback of spectral CNNs is their explicit assumption of an undirected graph, leading to a symmetric Laplacian matrix with orthogonal eigendecomposition. In this work we propose MotifNet, a graph CNN capable of dealing with directed graphs by exploiting local graph motifs. We present experimental evidence showing the advantage of our approach on real data.