MotifNet: a motif-based Graph Convolutional Network for directed graphs
Paper and Code
Feb 04, 2018
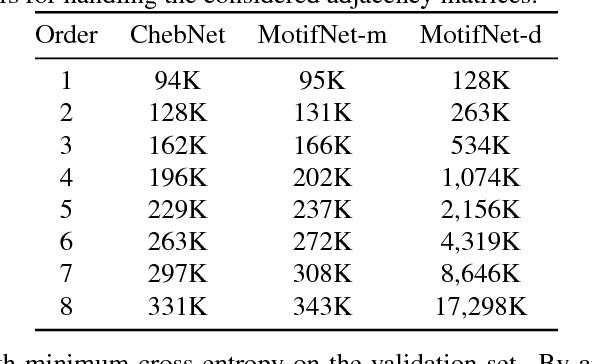
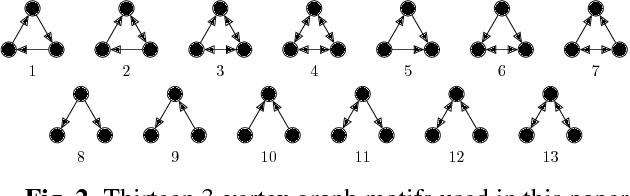
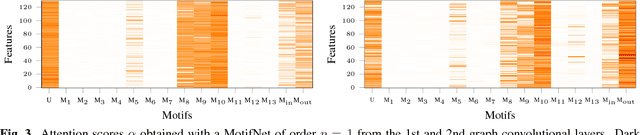
Deep learning on graphs and in particular, graph convolutional neural networks, have recently attracted significant attention in the machine learning community. Many of such techniques explore the analogy between the graph Laplacian eigenvectors and the classical Fourier basis, allowing to formulate the convolution as a multiplication in the spectral domain. One of the key drawback of spectral CNNs is their explicit assumption of an undirected graph, leading to a symmetric Laplacian matrix with orthogonal eigendecomposition. In this work we propose MotifNet, a graph CNN capable of dealing with directed graphs by exploiting local graph motifs. We present experimental evidence showing the advantage of our approach on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge