ResCP: Reservoir Conformal Prediction for Time Series Forecasting

Conformal prediction offers a powerful framework for building distribution-free prediction intervals for exchangeable data. Existing methods that extend conformal prediction to sequential data rely on fitting a relatively complex model to capture temporal dependencies. However, these methods can fail if the sample size is small and often require expensive retraining when the underlying data distribution changes. To overcome these limitations, we propose Reservoir Conformal Prediction (ResCP), a novel training-free conformal prediction method for time series. Our approach leverages the efficiency and representation learning capabilities of reservoir computing to dynamically reweight conformity scores. In particular, we compute similarity scores among reservoir states and use them to adaptively reweight the observed residuals at each step. With this approach, ResCP enables us to account for local temporal dynamics when modeling the error distribution without compromising computational scalability. We prove that, under reasonable assumptions, ResCP achieves asymptotic conditional coverage, and we empirically demonstrate its effectiveness across diverse forecasting tasks.

Amortized Sampling with Transferable Normalizing Flows

Efficient equilibrium sampling of molecular conformations remains a core challenge in computational chemistry and statistical inference. Classical approaches such as molecular dynamics or Markov chain Monte Carlo inherently lack amortization; the computational cost of sampling must be paid in-full for each system of interest. The widespread success of generative models has inspired interest into overcoming this limitation through learning sampling algorithms. Despite performing on par with conventional methods when trained on a single system, learned samplers have so far demonstrated limited ability to transfer across systems. We prove that deep learning enables the design of scalable and transferable samplers by introducing Prose, a 280 million parameter all-atom transferable normalizing flow trained on a corpus of peptide molecular dynamics trajectories up to 8 residues in length. Prose draws zero-shot uncorrelated proposal samples for arbitrary peptide systems, achieving the previously intractable transferability across sequence length, whilst retaining the efficient likelihood evaluation of normalizing flows. Through extensive empirical evaluation we demonstrate the efficacy of Prose as a proposal for a variety of sampling algorithms, finding a simple importance sampling-based finetuning procedure to achieve superior performance to established methods such as sequential Monte Carlo on unseen tetrapeptides. We open-source the Prose codebase, model weights, and training dataset, to further stimulate research into amortized sampling methods and finetuning objectives.

Over-squashing in Spatiotemporal Graph Neural Networks

Graph Neural Networks (GNNs) have achieved remarkable success across various domains. However, recent theoretical advances have identified fundamental limitations in their information propagation capabilities, such as over-squashing, where distant nodes fail to effectively exchange information. While extensively studied in static contexts, this issue remains unexplored in Spatiotemporal GNNs (STGNNs), which process sequences associated with graph nodes. Nonetheless, the temporal dimension amplifies this challenge by increasing the information that must be propagated. In this work, we formalize the spatiotemporal over-squashing problem and demonstrate its distinct characteristics compared to the static case. Our analysis reveals that counterintuitively, convolutional STGNNs favor information propagation from points temporally distant rather than close in time. Moreover, we prove that architectures that follow either time-and-space or time-then-space processing paradigms are equally affected by this phenomenon, providing theoretical justification for computationally efficient implementations. We validate our findings on synthetic and real-world datasets, providing deeper insights into their operational dynamics and principled guidance for more effective designs.

HYPER: A Foundation Model for Inductive Link Prediction with Knowledge Hypergraphs

Inductive link prediction with knowledge hypergraphs is the task of predicting missing hyperedges involving completely novel entities (i.e., nodes unseen during training). Existing methods for inductive link prediction with knowledge hypergraphs assume a fixed relational vocabulary and, as a result, cannot generalize to knowledge hypergraphs with novel relation types (i.e., relations unseen during training). Inspired by knowledge graph foundation models, we propose HYPER as a foundation model for link prediction, which can generalize to any knowledge hypergraph, including novel entities and novel relations. Importantly, HYPER can learn and transfer across different relation types of varying arities, by encoding the entities of each hyperedge along with their respective positions in the hyperedge. To evaluate HYPER, we construct 16 new inductive datasets from existing knowledge hypergraphs, covering a diverse range of relation types of varying arities. Empirically, HYPER consistently outperforms all existing methods in both node-only and node-and-relation inductive settings, showing strong generalization to unseen, higher-arity relational structures.

On Measuring Long-Range Interactions in Graph Neural Networks

Long-range graph tasks -- those dependent on interactions between distant nodes -- are an open problem in graph neural network research. Real-world benchmark tasks, especially the Long Range Graph Benchmark, have become popular for validating the long-range capability of proposed architectures. However, this is an empirical approach that lacks both robustness and theoretical underpinning; a more principled characterization of the long-range problem is required. To bridge this gap, we formalize long-range interactions in graph tasks, introduce a range measure for operators on graphs, and validate it with synthetic experiments. We then leverage our measure to examine commonly used tasks and architectures, and discuss to what extent they are, in fact, long-range. We believe our work advances efforts to define and address the long-range problem on graphs, and that our range measure will aid evaluation of new datasets and architectures.

Scalable Equilibrium Sampling with Sequential Boltzmann Generators

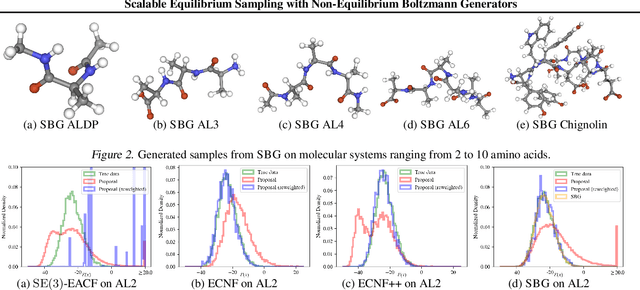
Scalable sampling of molecular states in thermodynamic equilibrium is a long-standing challenge in statistical physics. Boltzmann generators tackle this problem by pairing powerful normalizing flows with importance sampling to obtain statistically independent samples under the target distribution. In this paper, we extend the Boltzmann generator framework and introduce Sequential Boltzmann generators (SBG) with two key improvements. The first is a highly efficient non-equivariant Transformer-based normalizing flow operating directly on all-atom Cartesian coordinates. In contrast to equivariant continuous flows of prior methods, we leverage exactly invertible non-equivariant architectures which are highly efficient both during sample generation and likelihood computation. As a result, this unlocks more sophisticated inference strategies beyond standard importance sampling. More precisely, as a second key improvement we perform inference-time scaling of flow samples using annealed Langevin dynamics which transports samples toward the target distribution leading to lower variance (annealed) importance weights which enable higher fidelity resampling with sequential Monte Carlo. SBG achieves state-of-the-art performance w.r.t. all metrics on molecular systems, demonstrating the first equilibrium sampling in Cartesian coordinates of tri, tetra, and hexapeptides that were so far intractable for prior Boltzmann generators.

Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks

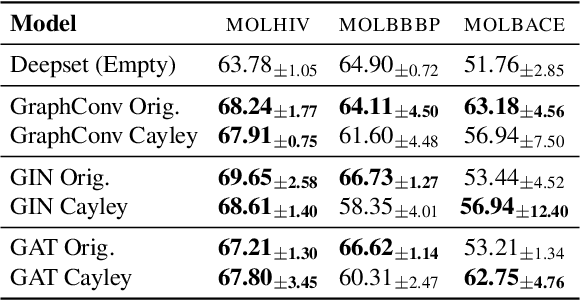
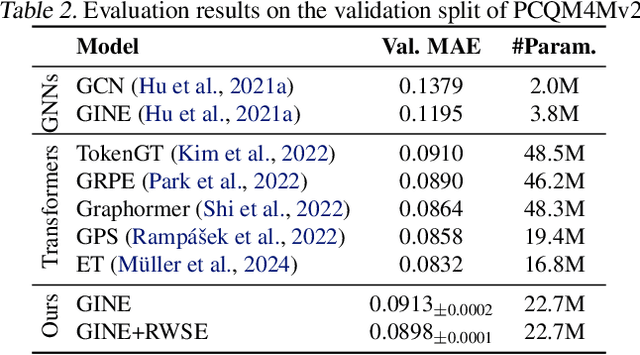
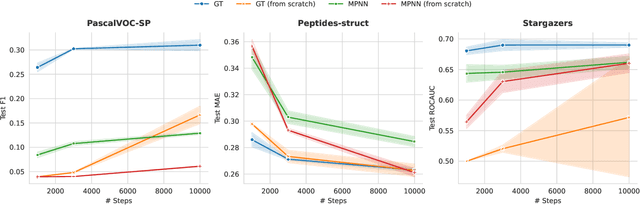
While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.

How Expressive are Knowledge Graph Foundation Models?

Knowledge Graph Foundation Models (KGFMs) are at the frontier for deep learning on knowledge graphs (KGs), as they can generalize to completely novel knowledge graphs with different relational vocabularies. Despite their empirical success, our theoretical understanding of KGFMs remains very limited. In this paper, we conduct a rigorous study of the expressive power of KGFMs. Specifically, we show that the expressive power of KGFMs directly depends on the motifs that are used to learn the relation representations. We then observe that the most typical motifs used in the existing literature are binary, as the representations are learned based on how pairs of relations interact, which limits the model's expressiveness. As part of our study, we design more expressive KGFMs using richer motifs, which necessitate learning relation representations based on, e.g., how triples of relations interact with each other. Finally, we empirically validate our theoretical findings, showing that the use of richer motifs results in better performance on a wide range of datasets drawn from different domains.

On the Limitations of Fractal Dimension as a Measure of Generalization

Bounding and predicting the generalization gap of overparameterized neural networks remains a central open problem in theoretical machine learning. Neural network optimization trajectories have been proposed to possess fractal structure, leading to bounds and generalization measures based on notions of fractal dimension on these trajectories. Prominently, both the Hausdorff dimension and the persistent homology dimension have been proposed to correlate with generalization gap, thus serving as a measure of generalization. This work performs an extended evaluation of these topological generalization measures. We demonstrate that fractal dimension fails to predict generalization of models trained from poor initializations. We further identify that the $\ell^2$ norm of the final parameter iterate, one of the simplest complexity measures in learning theory, correlates more strongly with the generalization gap than these notions of fractal dimension. Finally, our study reveals the intriguing manifestation of model-wise double descent in persistent homology-based generalization measures. This work lays the ground for a deeper investigation of the causal relationships between fractal geometry, topological data analysis, and neural network optimization.

Message-Passing Monte Carlo: Generating low-discrepancy point sets via Graph Neural Networks

Discrepancy is a well-known measure for the irregularity of the distribution of a point set. Point sets with small discrepancy are called low-discrepancy and are known to efficiently fill the space in a uniform manner. Low-discrepancy points play a central role in many problems in science and engineering, including numerical integration, computer vision, machine perception, computer graphics, machine learning, and simulation. In this work, we present the first machine learning approach to generate a new class of low-discrepancy point sets named Message-Passing Monte Carlo (MPMC) points. Motivated by the geometric nature of generating low-discrepancy point sets, we leverage tools from Geometric Deep Learning and base our model on Graph Neural Networks. We further provide an extension of our framework to higher dimensions, which flexibly allows the generation of custom-made points that emphasize the uniformity in specific dimensions that are primarily important for the particular problem at hand. Finally, we demonstrate that our proposed model achieves state-of-the-art performance superior to previous methods by a significant margin. In fact, MPMC points are empirically shown to be either optimal or near-optimal with respect to the discrepancy for every dimension and the number of points for which the optimal discrepancy can be determined.