On the Limitations of Fractal Dimension as a Measure of Generalization

Bounding and predicting the generalization gap of overparameterized neural networks remains a central open problem in theoretical machine learning. Neural network optimization trajectories have been proposed to possess fractal structure, leading to bounds and generalization measures based on notions of fractal dimension on these trajectories. Prominently, both the Hausdorff dimension and the persistent homology dimension have been proposed to correlate with generalization gap, thus serving as a measure of generalization. This work performs an extended evaluation of these topological generalization measures. We demonstrate that fractal dimension fails to predict generalization of models trained from poor initializations. We further identify that the $\ell^2$ norm of the final parameter iterate, one of the simplest complexity measures in learning theory, correlates more strongly with the generalization gap than these notions of fractal dimension. Finally, our study reveals the intriguing manifestation of model-wise double descent in persistent homology-based generalization measures. This work lays the ground for a deeper investigation of the causal relationships between fractal geometry, topological data analysis, and neural network optimization.

Tropical Expressivity of Neural Networks

We propose an algebraic geometric framework to study the expressivity of linear activation neural networks. A particular quantity that has been actively studied in the field of deep learning is the number of linear regions, which gives an estimate of the information capacity of the architecture. To study and evaluate information capacity and expressivity, we work in the setting of tropical geometry -- a combinatorial and polyhedral variant of algebraic geometry -- where there are known connections between tropical rational maps and feedforward neural networks. Our work builds on and expands this connection to capitalize on the rich theory of tropical geometry to characterize and study various architectural aspects of neural networks. Our contributions are threefold: we provide a novel tropical geometric approach to selecting sampling domains among linear regions; an algebraic result allowing for a guided restriction of the sampling domain for network architectures with symmetries; and an open source library to analyze neural networks as tropical Puiseux rational maps. We provide a comprehensive set of proof-of-concept numerical experiments demonstrating the breadth of neural network architectures to which tropical geometric theory can be applied to reveal insights on expressivity characteristics of a network. Our work provides the foundations for the adaptation of both theory and existing software from computational tropical geometry and symbolic computation to deep learning.

Computable Stability for Persistence Rank Function Machine Learning

Persistent homology barcodes and diagrams are a cornerstone of topological data analysis. Widely used in many real data settings, they relate variation in topological information (as measured by cellular homology) with variation in data, however, they are challenging to use in statistical settings due to their complex geometric structure. In this paper, we revisit the persistent homology rank function -- an invariant measure of ``shape" that was introduced before barcodes and persistence diagrams and captures the same information in a form that is more amenable to data and computation. In particular, since they are functions, techniques from functional data analysis -- a domain of statistics adapted for functions -- apply directly to persistent homology when represented by rank functions. Rank functions, however, have been less popular than barcodes because they face the challenge that stability -- a property that is crucial to validate their use in data analysis -- is difficult to guarantee, mainly due to metric concerns on rank function space. However, rank functions extend more naturally to the increasingly popular and important case of multiparameter persistent homology. In this paper, we study the performance of rank functions in functional inferential statistics and machine learning on both simulated and real data, and in both single and multiparameter persistent homology. We find that the use of persistent homology captured by rank functions offers a clear improvement over existing approaches. We then provide theoretical justification for our numerical experiments and applications to data by deriving several stability results for single- and multiparameter persistence rank functions under various metrics with the underlying aim of computational feasibility and interpretability.

$k$-Means Clustering for Persistent Homology

Persistent homology is a fundamental methodology from topological data analysis that summarizes the lifetimes of topological features within a dataset as a persistence diagram; it has recently gained much popularity from its myriad successful applications to many domains. However, a significant challenge to its widespread implementation, especially in statistical methodology and machine learning algorithms, is the format of the persistence diagram as a multiset of half-open intervals. In this paper, we comprehensively study $k$-means clustering where the input is various embeddings of persistence diagrams, as well as persistence diagrams themselves and their generalizations as persistence measures. We show that the clustering performance directly on persistence diagrams and measures far outperform their vectorized representations, despite their more complex representations. Moreover, we prove convergence of the algorithm on persistence diagram space and establish theoretical properties of the solution to the optimization problem in the Karush--Kuhn--Tucker framework.

Fast Topological Signal Identification and Persistent Cohomological Cycle Matching

Within the context of topological data analysis, the problems of identifying topological significance and matching signals across datasets are important and useful inferential tasks in many applications. The limitation of existing solutions to these problems, however, is computational speed. In this paper, we harness the state-of-the-art for persistent homology computation by studying the problem of determining topological prevalence and cycle matching using a cohomological approach, which increases their feasibility and applicability to a wider variety of applications and contexts. We demonstrate this on a wide range of real-life, large-scale, and complex datasets. We extend existing notions of topological prevalence and cycle matching to include general non-Morse filtrations. This provides the most general and flexible state-of-the-art adaptation of topological signal identification and persistent cycle matching, which performs comparisons of orders of ten for thousands of sampled points in a matter of minutes on standard institutional HPC CPU facilities.

Learning Linear Non-Gaussian Polytree Models

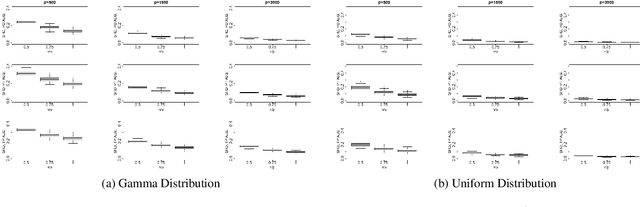
In the context of graphical causal discovery, we adapt the versatile framework of linear non-Gaussian acyclic models (LiNGAMs) to propose new algorithms to efficiently learn graphs that are polytrees. Our approach combines the Chow--Liu algorithm, which first learns the undirected tree structure, with novel schemes to orient the edges. The orientation schemes assess algebraic relations among moments of the data-generating distribution and are computationally inexpensive. We establish high-dimensional consistency results for our approach and compare different algorithmic versions in numerical experiments.

Rewiring Networks for Graph Neural Network Training Using Discrete Geometry

Information over-squashing is a phenomenon of inefficient information propagation between distant nodes on networks. It is an important problem that is known to significantly impact the training of graph neural networks (GNNs), as the receptive field of a node grows exponentially. To mitigate this problem, a preprocessing procedure known as rewiring is often applied to the input network. In this paper, we investigate the use of discrete analogues of classical geometric notions of curvature to model information flow on networks and rewire them. We show that these classical notions achieve state-of-the-art performance in GNN training accuracy on a variety of real-world network datasets. Moreover, compared to the current state-of-the-art, these classical notions exhibit a clear advantage in computational runtime by several orders of magnitude.

Approximating Persistent Homology for Large Datasets

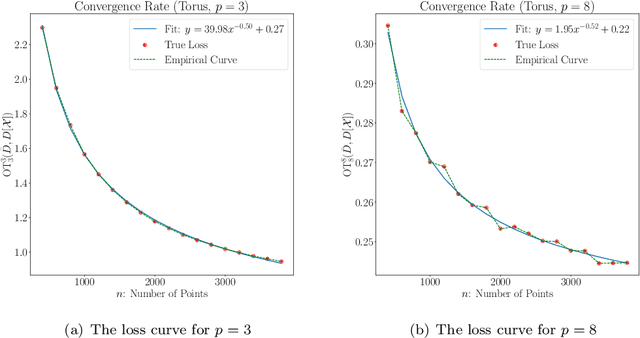
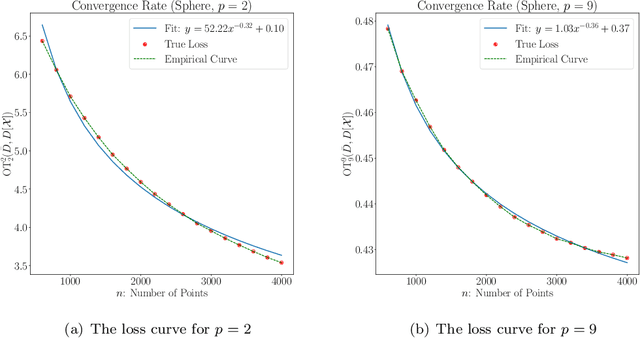
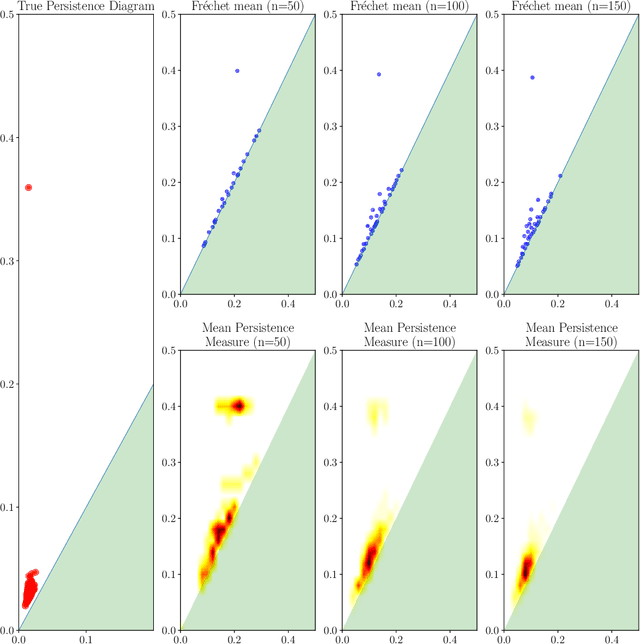
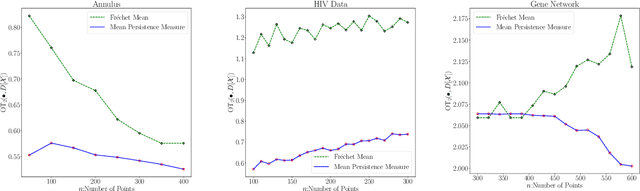
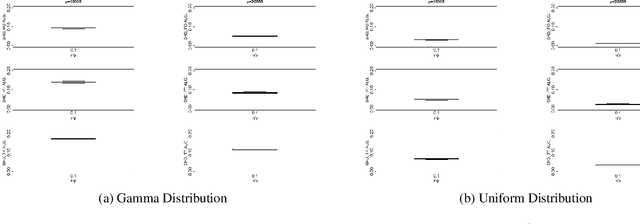
Persistent homology is an important methodology from topological data analysis which adapts theory from algebraic topology to data settings and has been successfully implemented in many applications. It produces a statistical summary in the form of a persistence diagram, which captures the shape and size of the data. Despite its widespread use, persistent homology is simply impossible to implement when a dataset is very large. In this paper we address the problem of finding a representative persistence diagram for prohibitively large datasets. We adapt the classical statistical method of bootstrapping, namely, drawing and studying smaller multiple subsamples from the large dataset. We show that the mean of the persistence diagrams of subsamples -- taken as a mean persistence measure computed from the subsamples -- is a valid approximation of the true persistent homology of the larger dataset. We give the rate of convergence of the mean persistence diagram to the true persistence diagram in terms of the number of subsamples and size of each subsample. Given the complex algebraic and geometric nature of persistent homology, we adapt the convexity and stability properties in the space of persistence diagrams together with random set theory to achieve our theoretical results for the general setting of point cloud data. We demonstrate our approach on simulated and real data, including an application of shape clustering on complex large-scale point cloud data.

Curved Markov Chain Monte Carlo for Network Learning

We present a geometrically enhanced Markov chain Monte Carlo sampler for networks based on a discrete curvature measure defined on graphs. Specifically, we incorporate the concept of graph Forman curvature into sampling procedures on both the nodes and edges of a network explicitly, via the transition probability of the Markov chain, as well as implicitly, via the target stationary distribution, which gives a novel, curved Markov chain Monte Carlo approach to learning networks. We show that integrating curvature into the sampler results in faster convergence to a wide range of network statistics demonstrated on deterministic networks drawn from real-world data.

Topological Data Analysis of Database Representations for Information Retrieval

Appropriately representing elements in a database so that queries may be accurately matched is a central task in information retrieval. This recently has been achieved by embedding the graphical structure of the database into a manifold so that the hierarchy is preserved. Persistent homology provides a rigorous characterization for the database topology in terms of both its hierarchy and connectivity structure. We compute persistent homology on a variety of datasets and show that some commonly used embeddings fail to preserve the connectivity. Moreover, we show that embeddings which successfully retain the database topology coincide in persistent homology. We introduce the dilation-invariant bottleneck distance to capture this effect, which addresses metric distortion on manifolds. We use it to show that distances between topology-preserving embeddings of databases are small.