Causal Effect Identification in lvLiNGAM from Higher-Order Cumulants

This paper investigates causal effect identification in latent variable Linear Non-Gaussian Acyclic Models (lvLiNGAM) using higher-order cumulants, addressing two prominent setups that are challenging in the presence of latent confounding: (1) a single proxy variable that may causally influence the treatment and (2) underspecified instrumental variable cases where fewer instruments exist than treatments. We prove that causal effects are identifiable with a single proxy or instrument and provide corresponding estimation methods. Experimental results demonstrate the accuracy and robustness of our approaches compared to existing methods, advancing the theoretical and practical understanding of causal inference in linear systems with latent confounders.

Nonlinear Causal Discovery for Grouped Data

Inferring cause-effect relationships from observational data has gained significant attention in recent years, but most methods are limited to scalar random variables. In many important domains, including neuroscience, psychology, social science, and industrial manufacturing, the causal units of interest are groups of variables rather than individual scalar measurements. Motivated by these applications, we extend nonlinear additive noise models to handle random vectors, establishing a two-step approach for causal graph learning: First, infer the causal order among random vectors. Second, perform model selection to identify the best graph consistent with this order. We introduce effective and novel solutions for both steps in the vector case, demonstrating strong performance in simulations. Finally, we apply our method to real-world assembly line data with partial knowledge of causal ordering among variable groups.

Robust Score Matching

Proposed in Hyv\"arinen (2005), score matching is a parameter estimation procedure that does not require computation of distributional normalizing constants. In this work we utilize the geometric median of means to develop a robust score matching procedure that yields consistent parameter estimates in settings where the observed data has been contaminated. A special appeal of the proposed method is that it retains convexity in exponential family models. The new method is therefore particularly attractive for non-Gaussian, exponential family graphical models where evaluation of normalizing constants is intractable. Support recovery guarantees for such models when contamination is present are provided. Additionally, support recovery is studied in numerical experiments and on a precipitation dataset. We demonstrate that the proposed robust score matching estimator performs comparably to the standard score matching estimator when no contamination is present but greatly outperforms this estimator in a setting with contamination.

Kernel-Based Differentiable Learning of Non-Parametric Directed Acyclic Graphical Models

Causal discovery amounts to learning a directed acyclic graph (DAG) that encodes a causal model. This model selection problem can be challenging due to its large combinatorial search space, particularly when dealing with non-parametric causal models. Recent research has sought to bypass the combinatorial search by reformulating causal discovery as a continuous optimization problem, employing constraints that ensure the acyclicity of the graph. In non-parametric settings, existing approaches typically rely on finite-dimensional approximations of the relationships between nodes, resulting in a score-based continuous optimization problem with a smooth acyclicity constraint. In this work, we develop an alternative approximation method by utilizing reproducing kernel Hilbert spaces (RKHS) and applying general sparsity-inducing regularization terms based on partial derivatives. Within this framework, we introduce an extended RKHS representer theorem. To enforce acyclicity, we advocate the log-determinant formulation of the acyclicity constraint and show its stability. Finally, we assess the performance of our proposed RKHS-DAGMA procedure through simulations and illustrative data analyses.

Causal Effect Identification in LiNGAM Models with Latent Confounders

We study the generic identifiability of causal effects in linear non-Gaussian acyclic models (LiNGAM) with latent variables. We consider the problem in two main settings: When the causal graph is known a priori, and when it is unknown. In both settings, we provide a complete graphical characterization of the identifiable direct or total causal effects among observed variables. Moreover, we propose efficient algorithms to certify the graphical conditions. Finally, we propose an adaptation of the reconstruction independent component analysis (RICA) algorithm that estimates the causal effects from the observational data given the causal graph. Experimental results show the effectiveness of the proposed method in estimating the causal effects.

Parameter identification in linear non-Gaussian causal models under general confounding

Linear non-Gaussian causal models postulate that each random variable is a linear function of parent variables and non-Gaussian exogenous error terms. We study identification of the linear coefficients when such models contain latent variables. Our focus is on the commonly studied acyclic setting, where each model corresponds to a directed acyclic graph (DAG). For this case, prior literature has demonstrated that connections to overcomplete independent component analysis yield effective criteria to decide parameter identifiability in latent variable models. However, this connection is based on the assumption that the observed variables linearly depend on the latent variables. Departing from this assumption, we treat models that allow for arbitrary non-linear latent confounding. Our main result is a graphical criterion that is necessary and sufficient for deciding the generic identifiability of direct causal effects. Moreover, we provide an algorithmic implementation of the criterion with a run time that is polynomial in the number of observed variables. Finally, we report on estimation heuristics based on the identification result, explore a generalization to models with feedback loops, and provide new results on the identifiability of the causal graph.

$\texttt{causalAssembly}$: Generating Realistic Production Data for Benchmarking Causal Discovery

Algorithms for causal discovery have recently undergone rapid advances and increasingly draw on flexible nonparametric methods to process complex data. With these advances comes a need for adequate empirical validation of the causal relationships learned by different algorithms. However, for most real data sources true causal relations remain unknown. This issue is further compounded by privacy concerns surrounding the release of suitable high-quality data. To help address these challenges, we gather a complex dataset comprising measurements from an assembly line in a manufacturing context. This line consists of numerous physical processes for which we are able to provide ground truth causal relationships on the basis of a detailed study of the underlying physics. We use the assembly line data and associated ground truth information to build a system for generation of semisynthetic manufacturing data that supports benchmarking of causal discovery methods. To accomplish this, we employ distributional random forests in order to flexibly estimate and represent conditional distributions that may be combined into joint distributions that strictly adhere to a causal model over the observed variables. The estimated conditionals and tools for data generation are made available in our Python library $\texttt{causalAssembly}$. Using the library, we showcase how to benchmark several well-known causal discovery algorithms.

Rank-Based Causal Discovery for Post-Nonlinear Models

Learning causal relationships from empirical observations is a central task in scientific research. A common method is to employ structural causal models that postulate noisy functional relations among a set of interacting variables. To ensure unique identifiability of causal directions, researchers consider restricted subclasses of structural causal models. Post-nonlinear (PNL) causal models constitute one of the most flexible options for such restricted subclasses, containing in particular the popular additive noise models as a further subclass. However, learning PNL models is not well studied beyond the bivariate case. The existing methods learn non-linear functional relations by minimizing residual dependencies and subsequently test independence from residuals to determine causal orientations. However, these methods can be prone to overfitting and, thus, difficult to tune appropriately in practice. As an alternative, we propose a new approach for PNL causal discovery that uses rank-based methods to estimate the functional parameters. This new approach exploits natural invariances of PNL models and disentangles the estimation of the non-linear functions from the independence tests used to find causal orientations. We prove consistency of our method and validate our results in numerical experiments.

Unpaired Multi-Domain Causal Representation Learning

The goal of causal representation learning is to find a representation of data that consists of causally related latent variables. We consider a setup where one has access to data from multiple domains that potentially share a causal representation. Crucially, observations in different domains are assumed to be unpaired, that is, we only observe the marginal distribution in each domain but not their joint distribution. In this paper, we give sufficient conditions for identifiability of the joint distribution and the shared causal graph in a linear setup. Identifiability holds if we can uniquely recover the joint distribution and the shared causal representation from the marginal distributions in each domain. We transform our identifiability results into a practical method to recover the shared latent causal graph. Moreover, we study how multiple domains reduce errors in falsely detecting shared causal variables in the finite data setting.

High-Dimensional Undirected Graphical Models for Arbitrary Mixed Data

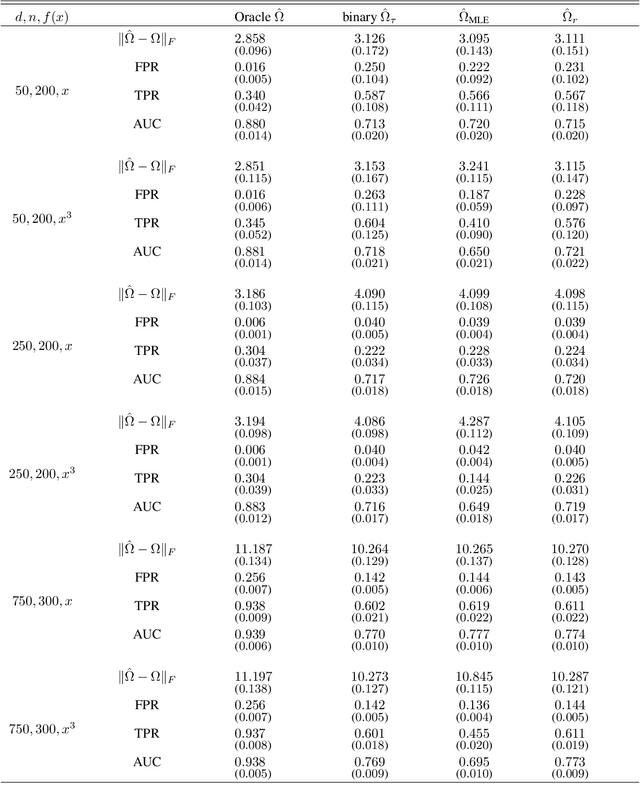
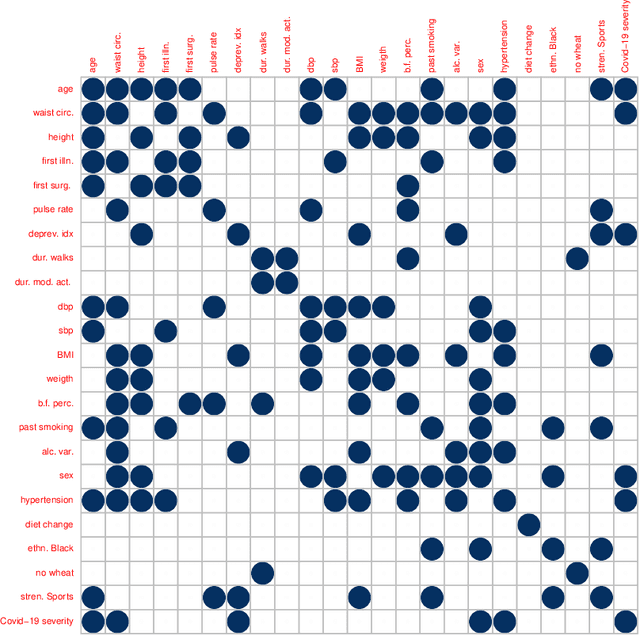
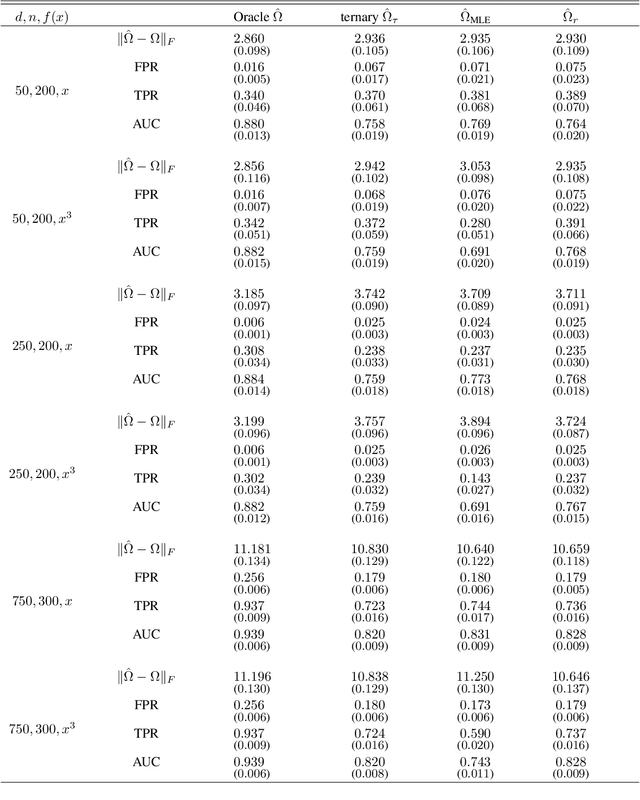
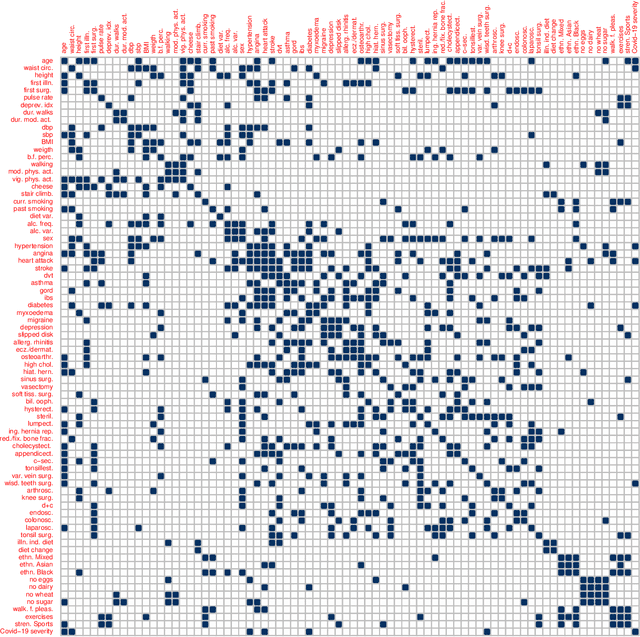
Graphical models are an important tool in exploring relationships between variables in complex, multivariate data. Methods for learning such graphical models are well developed in the case where all variables are either continuous or discrete, including in high-dimensions. However, in many applications data span variables of different types (e.g. continuous, count, binary, ordinal, etc.), whose principled joint analysis is nontrivial. Latent Gaussian copula models, in which all variables are modeled as transformations of underlying jointly Gaussian variables, represent a useful approach. Recent advances have shown how the binary-continuous case can be tackled, but the general mixed variable type regime remains challenging. In this work, we make the simple yet useful observation that classical ideas concerning polychoric and polyserial correlations can be leveraged in a latent Gaussian copula framework. Building on this observation we propose flexible and scalable methodology for data with variables of entirely general mixed type. We study the key properties of the approaches theoretically and empirically, via extensive simulations as well an illustrative application to data from the UK Biobank concerning COVID-19 risk factors.