Causal Effect Identification in LiNGAM Models with Latent Confounders

We study the generic identifiability of causal effects in linear non-Gaussian acyclic models (LiNGAM) with latent variables. We consider the problem in two main settings: When the causal graph is known a priori, and when it is unknown. In both settings, we provide a complete graphical characterization of the identifiable direct or total causal effects among observed variables. Moreover, we propose efficient algorithms to certify the graphical conditions. Finally, we propose an adaptation of the reconstruction independent component analysis (RICA) algorithm that estimates the causal effects from the observational data given the causal graph. Experimental results show the effectiveness of the proposed method in estimating the causal effects.

On Identifiability of Conditional Causal Effects

We address the problem of identifiability of an arbitrary conditional causal effect given both the causal graph and a set of any observational and/or interventional distributions of the form $Q[S]:=P(S|do(V\setminus S))$, where $V$ denotes the set of all observed variables and $S\subseteq V$. We call this problem conditional generalized identifiability (c-gID in short) and prove the completeness of Pearl's $do$-calculus for the c-gID problem by providing sound and complete algorithm for the c-gID problem. This work revisited the c-gID problem in Lee et al. [2020], Correa et al. [2021] by adding explicitly the positivity assumption which is crucial for identifiability. It extends the results of [Lee et al., 2019, Kivva et al., 2022] on general identifiability (gID) which studied the problem for unconditional causal effects and Shpitser and Pearl [2006b] on identifiability of conditional causal effects given merely the observational distribution $P(\mathbf{V})$ as our algorithm generalizes the algorithms proposed in [Kivva et al., 2022] and [Shpitser and Pearl, 2006b].

Revisiting the General Identifiability Problem

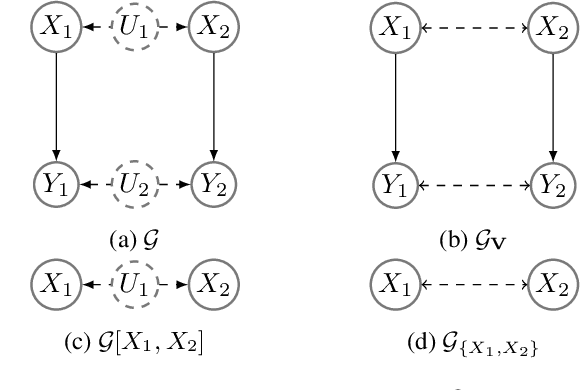
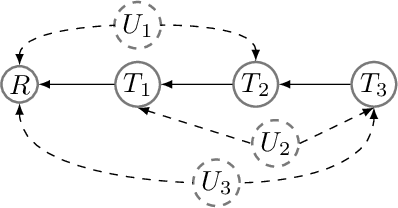
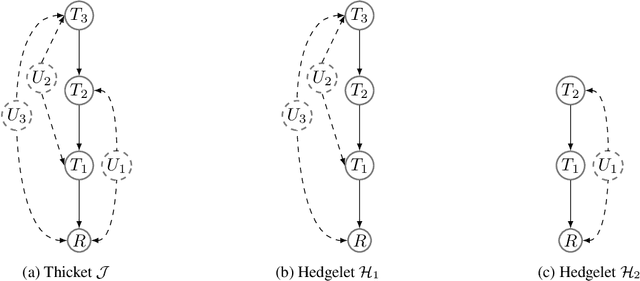
We revisit the problem of general identifiability originally introduced in [Lee et al., 2019] for causal inference and note that it is necessary to add positivity assumption of observational distribution to the original definition of the problem. We show that without such an assumption the rules of do-calculus and consequently the proposed algorithm in [Lee et al., 2019] are not sound. Moreover, adding the assumption will cause the completeness proof in [Lee et al., 2019] to fail. Under positivity assumption, we present a new algorithm that is provably both sound and complete. A nice property of this new algorithm is that it establishes a connection between general identifiability and classical identifiability by Pearl [1995] through decomposing the general identifiability problem into a series of classical identifiability sub-problems.