Causal Effect Identification in lvLiNGAM from Higher-Order Cumulants

This paper investigates causal effect identification in latent variable Linear Non-Gaussian Acyclic Models (lvLiNGAM) using higher-order cumulants, addressing two prominent setups that are challenging in the presence of latent confounding: (1) a single proxy variable that may causally influence the treatment and (2) underspecified instrumental variable cases where fewer instruments exist than treatments. We prove that causal effects are identifiable with a single proxy or instrument and provide corresponding estimation methods. Experimental results demonstrate the accuracy and robustness of our approaches compared to existing methods, advancing the theoretical and practical understanding of causal inference in linear systems with latent confounders.

Best Group Identification in Multi-Objective Bandits

We introduce the Best Group Identification problem in a multi-objective multi-armed bandit setting, where an agent interacts with groups of arms with vector-valued rewards. The performance of a group is determined by an efficiency vector which represents the group's best attainable rewards across different dimensions. The objective is to identify the set of optimal groups in the fixed-confidence setting. We investigate two key formulations: group Pareto set identification, where efficiency vectors of optimal groups are Pareto optimal and linear best group identification, where each reward dimension has a known weight and the optimal group maximizes the weighted sum of its efficiency vector's entries. For both settings, we propose elimination-based algorithms, establish upper bounds on their sample complexity, and derive lower bounds that apply to any correct algorithm. Through numerical experiments, we demonstrate the strong empirical performance of the proposed algorithms.

Multi-Domain Causal Discovery in Bijective Causal Models

We consider the problem of causal discovery (a.k.a., causal structure learning) in a multi-domain setting. We assume that the causal functions are invariant across the domains, while the distribution of the exogenous noise may vary. Under causal sufficiency (i.e., no confounders exist), we show that the causal diagram can be discovered under less restrictive functional assumptions compared to previous work. What enables causal discovery in this setting is bijective generation mechanisms (BGM), which ensures that the functional relation between the exogenous noise $E$ and the endogenous variable $Y$ is bijective and differentiable in both directions at every level of the cause variable $X = x$. BGM generalizes a variety of models including additive noise model, LiNGAM, post-nonlinear model, and location-scale noise model. Further, we derive a statistical test to find the parents set of the target variable. Experiments on various synthetic and real-world datasets validate our theoretical findings.

Graph-Dependent Regret Bounds in Multi-Armed Bandits with Interference

Multi-armed bandits (MABs) are frequently used for online sequential decision-making in applications ranging from recommending personalized content to assigning treatments to patients. A recurring challenge in the applicability of the classic MAB framework to real-world settings is ignoring \textit{interference}, where a unit's outcome depends on treatment assigned to others. This leads to an exponentially growing action space, rendering standard approaches computationally impractical. We study the MAB problem under network interference, where each unit's reward depends on its own treatment and those of its neighbors in a given interference graph. We propose a novel algorithm that uses the local structure of the interference graph to minimize regret. We derive a graph-dependent upper bound on cumulative regret showing that it improves over prior work. Additionally, we provide the first lower bounds for bandits with arbitrary network interference, where each bound involves a distinct structural property of the interference graph. These bounds demonstrate that when the graph is either dense or sparse, our algorithm is nearly optimal, with upper and lower bounds that match up to logarithmic factors. We complement our theoretical results with numerical experiments, which show that our approach outperforms baseline methods.

Sample Complexity of Nonparametric Closeness Testing for Continuous Distributions and Its Application to Causal Discovery with Hidden Confounding

We study the problem of closeness testing for continuous distributions and its implications for causal discovery. Specifically, we analyze the sample complexity of distinguishing whether two multidimensional continuous distributions are identical or differ by at least $\epsilon$ in terms of Kullback-Leibler (KL) divergence under non-parametric assumptions. To this end, we propose an estimator of KL divergence which is based on the von Mises expansion. Our closeness test attains optimal parametric rates under smoothness assumptions. Equipped with this test, which serves as a building block of our causal discovery algorithm to identify the causal structure between two multidimensional random variables, we establish sample complexity guarantees for our causal discovery method. To the best of our knowledge, this work is the first work that provides sample complexity guarantees for distinguishing cause and effect in multidimensional non-linear models with non-Gaussian continuous variables in the presence of unobserved confounding.

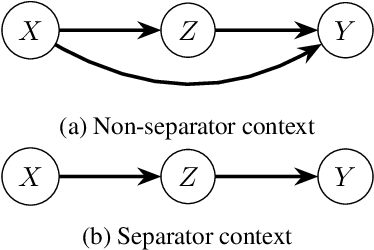
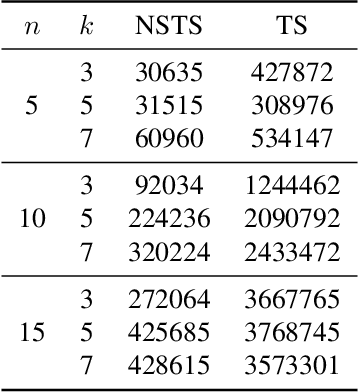
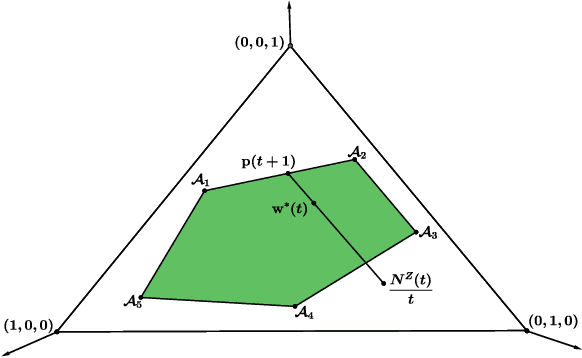
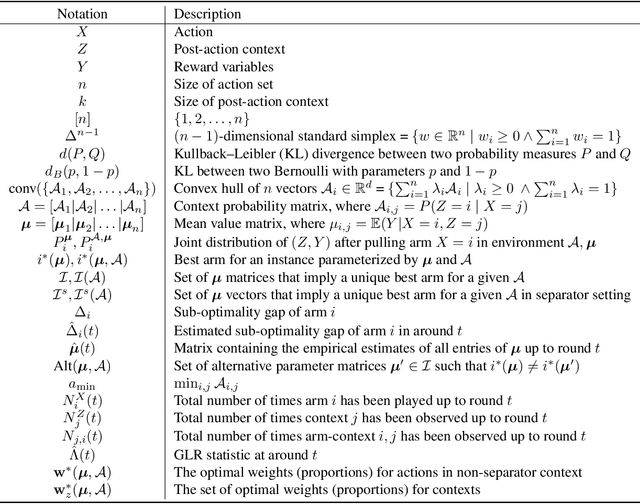
Optimal Best Arm Identification with Post-Action Context

We introduce the problem of best arm identification (BAI) with post-action context, a new BAI problem in a stochastic multi-armed bandit environment and the fixed-confidence setting. The problem addresses the scenarios in which the learner receives a $\textit{post-action context}$ in addition to the reward after playing each action. This post-action context provides additional information that can significantly facilitate the decision process. We analyze two different types of the post-action context: (i) $\textit{non-separator}$, where the reward depends on both the action and the context, and (ii) $\textit{separator}$, where the reward depends solely on the context. For both cases, we derive instance-dependent lower bounds on the sample complexity and propose algorithms that asymptotically achieve the optimal sample complexity. For the non-separator setting, we do so by demonstrating that the Track-and-Stop algorithm can be extended to this setting. For the separator setting, we propose a novel sampling rule called $\textit{G-tracking}$, which uses the geometry of the context space to directly track the contexts rather than the actions. Finally, our empirical results showcase the advantage of our approaches compared to the state of the art.

Multi-armed Bandits with Missing Outcome

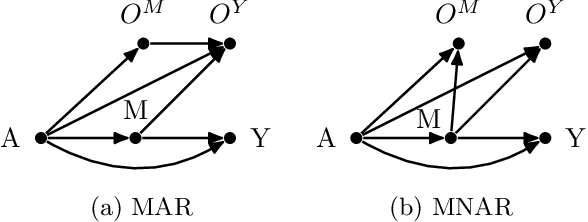
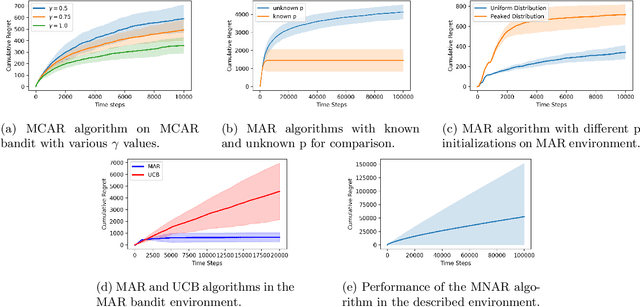
While significant progress has been made in designing algorithms that minimize regret in online decision-making, real-world scenarios often introduce additional complexities, perhaps the most challenging of which is missing outcomes. Overlooking this aspect or simply assuming random missingness invariably leads to biased estimates of the rewards and may result in linear regret. Despite the practical relevance of this challenge, no rigorous methodology currently exists for systematically handling missingness, especially when the missingness mechanism is not random. In this paper, we address this gap in the context of multi-armed bandits (MAB) with missing outcomes by analyzing the impact of different missingness mechanisms on achievable regret bounds. We introduce algorithms that account for missingness under both missing at random (MAR) and missing not at random (MNAR) models. Through both analytical and simulation studies, we demonstrate the drastic improvements in decision-making by accounting for missingness in these settings.

QWO: Speeding Up Permutation-Based Causal Discovery in LiGAMs

Causal discovery is essential for understanding relationships among variables of interest in many scientific domains. In this paper, we focus on permutation-based methods for learning causal graphs in Linear Gaussian Acyclic Models (LiGAMs), where the permutation encodes a causal ordering of the variables. Existing methods in this setting are not scalable due to their high computational complexity. These methods are comprised of two main components: (i) constructing a specific DAG, $\mathcal{G}^\pi$, for a given permutation $\pi$, which represents the best structure that can be learned from the available data while adhering to $\pi$, and (ii) searching over the space of permutations (i.e., causal orders) to minimize the number of edges in $\mathcal{G}^\pi$. We introduce QWO, a novel approach that significantly enhances the efficiency of computing $\mathcal{G}^\pi$ for a given permutation $\pi$. QWO has a speed-up of $O(n^2)$ ($n$ is the number of variables) compared to the state-of-the-art BIC-based method, making it highly scalable. We show that our method is theoretically sound and can be integrated into existing search strategies such as GRASP and hill-climbing-based methods to improve their performance.

Complexity of Minimizing Projected-Gradient-Dominated Functions with Stochastic First-order Oracles

This work investigates the performance limits of projected stochastic first-order methods for minimizing functions under the $(\alpha,\tau,\mathcal{X})$-projected-gradient-dominance property, that asserts the sub-optimality gap $F(\mathbf{x})-\min_{\mathbf{x}'\in \mathcal{X}}F(\mathbf{x}')$ is upper-bounded by $\tau\cdot\|\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})\|^{\alpha}$ for some $\alpha\in[1,2)$ and $\tau>0$ and $\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})$ is the projected-gradient mapping with $\eta>0$ as a parameter. For non-convex functions, we show that the complexity lower bound of querying a batch smooth first-order stochastic oracle to obtain an $\epsilon$-global-optimum point is $\Omega(\epsilon^{-{2}/{\alpha}})$. Furthermore, we show that a projected variance-reduced first-order algorithm can obtain the upper complexity bound of $\mathcal{O}(\epsilon^{-{2}/{\alpha}})$, matching the lower bound. For convex functions, we establish a complexity lower bound of $\Omega(\log(1/\epsilon)\cdot\epsilon^{-{2}/{\alpha}})$ for minimizing functions under a local version of gradient-dominance property, which also matches the upper complexity bound of accelerated stochastic subgradient methods.

Causal Discovery in Linear Models with Unobserved Variables and Measurement Error

The presence of unobserved common causes and the presence of measurement error are two of the most limiting challenges in the task of causal structure learning. Ignoring either of the two challenges can lead to detecting spurious causal links among variables of interest. In this paper, we study the problem of causal discovery in systems where these two challenges can be present simultaneously. We consider linear models which include four types of variables: variables that are directly observed, variables that are not directly observed but are measured with error, the corresponding measurements, and variables that are neither observed nor measured. We characterize the extent of identifiability of such model under separability condition (i.e., the matrix indicating the independent exogenous noise terms pertaining to the observed variables is identifiable) together with two versions of faithfulness assumptions and propose a notion of observational equivalence. We provide graphical characterization of the models that are equivalent and present a recovery algorithm that could return models equivalent to the ground truth.