Select-then-differentiate: Solving Bilevel Optimization with Manifold Lower-level Solution Sets

We study optimistic bilevel optimization when the lower-level problem has a non-isolated manifold of minimizers. In this setting, the hyper-objective may be non-differentiable because the upper-level criterion must choose among multiple lower-level solutions. Under a local Polyak--Łojasiewicz (PŁ) condition, we show that differentiability does not require the lower-level solution set to be a singleton: uniqueness of the optimistic selection is sufficient. This yields an explicit pseudoinverse-based hyper-gradient formula extending the classical singleton-minimizer result. We further characterize the regularity of the hyper-objective: non-degeneracy of the selected minimizer along the solution manifold yields local smoothness, while failure of uniqueness can create many non-differentiable points and failure of non-degeneracy can destroy all positive Hölder regularity of the hyper-gradient. Motivated by this theory, we propose HG-MS, a select-then-differentiate method combining explicit optimistic selection with efficient pseudoinverse-based hyper-gradient computation. Despite the nonconvex nature of optimistic selection over the lower-level solution manifold, we show that HG-MS converges to a stationary point of the optimistic objective with complexity governed by the intrinsic dimension of the solution manifold rather than its ambient dimension. Empirically, we test a practical variant of HG-MS for matched-budget LLM source reweighting. This variant preserves the select-then-differentiate principle and obtains the best GSM8K/MATH scores across the tested backbones, along with competitive or best MT-Bench instruction-following results.

Zeroth-Order Stackelberg Control in Combinatorial Congestion Games

We study Stackelberg (leader--follower) tuning of network parameters (tolls, capacities, incentives) in combinatorial congestion games, where selfish users choose discrete routes (or other combinatorial strategies) and settle at a congestion equilibrium. The leader minimizes a system-level objective (e.g., total travel time) evaluated at equilibrium, but this objective is typically nonsmooth because the set of used strategies can change abruptly. We propose ZO-Stackelberg, which couples a projection-free Frank--Wolfe equilibrium solver with a zeroth-order outer update, avoiding differentiation through equilibria. We prove convergence to generalized Goldstein stationary points of the true equilibrium objective, with explicit dependence on the equilibrium approximation error, and analyze subsampled oracles: if an exact minimizer is sampled with probability $κ_m$, then the Frank--Wolfe error decays as $\mathcal{O}(1/(κ_m T))$. We also propose stratified sampling as a practical way to avoid a vanishing $κ_m$ when the strategies that matter most for the Wardrop equilibrium concentrate in a few dominant combinatorial classes (e.g., short paths). Experiments on real-world networks demonstrate that our method achieves orders-of-magnitude speedups over a differentiation-based baseline while converging to follower equilibria.

Complexity of Minimizing Projected-Gradient-Dominated Functions with Stochastic First-order Oracles

This work investigates the performance limits of projected stochastic first-order methods for minimizing functions under the $(\alpha,\tau,\mathcal{X})$-projected-gradient-dominance property, that asserts the sub-optimality gap $F(\mathbf{x})-\min_{\mathbf{x}'\in \mathcal{X}}F(\mathbf{x}')$ is upper-bounded by $\tau\cdot\|\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})\|^{\alpha}$ for some $\alpha\in[1,2)$ and $\tau>0$ and $\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})$ is the projected-gradient mapping with $\eta>0$ as a parameter. For non-convex functions, we show that the complexity lower bound of querying a batch smooth first-order stochastic oracle to obtain an $\epsilon$-global-optimum point is $\Omega(\epsilon^{-{2}/{\alpha}})$. Furthermore, we show that a projected variance-reduced first-order algorithm can obtain the upper complexity bound of $\mathcal{O}(\epsilon^{-{2}/{\alpha}})$, matching the lower bound. For convex functions, we establish a complexity lower bound of $\Omega(\log(1/\epsilon)\cdot\epsilon^{-{2}/{\alpha}})$ for minimizing functions under a local version of gradient-dominance property, which also matches the upper complexity bound of accelerated stochastic subgradient methods.

Learning Algorithm Generalization Error Bounds via Auxiliary Distributions

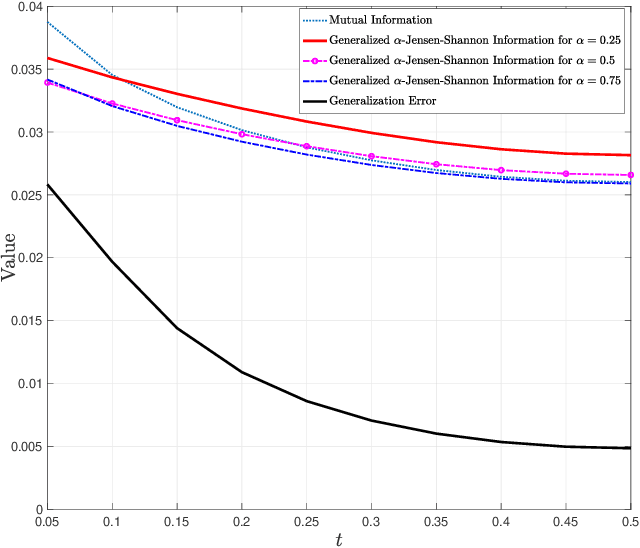
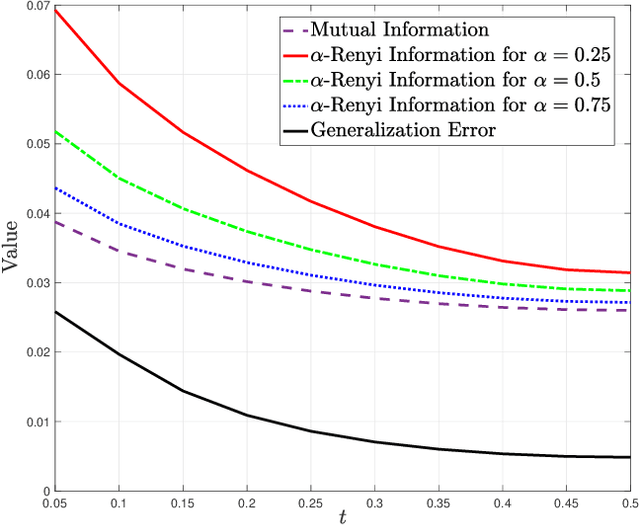
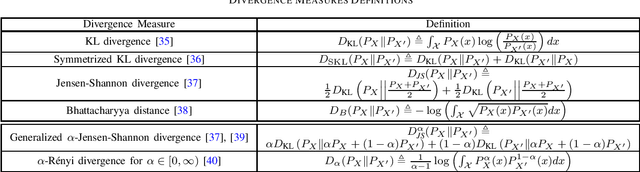
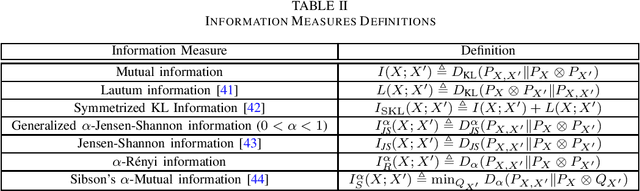
Generalization error boundaries are essential for comprehending how well machine learning models work. In this work, we suggest a creative method, i.e., the Auxiliary Distribution Method, that derives new upper bounds on generalization errors that are appropriate for supervised learning scenarios. We show that our general upper bounds can be specialized under some conditions to new bounds involving the generalized $\alpha$-Jensen-Shannon, $\alpha$-R\'enyi ($0< \alpha < 1$) information between random variable modeling the set of training samples and another random variable modeling the set of hypotheses. Our upper bounds based on generalized $\alpha$-Jensen-Shannon information are also finite. Additionally, we demonstrate how our auxiliary distribution method can be used to derive the upper bounds on generalization error under the distribution mismatch scenario in supervised learning algorithms, where the distributional mismatch is modeled as $\alpha$-Jensen-Shannon or $\alpha$-R\'enyi ($0< \alpha < 1$) between the distribution of test and training data samples. We also outline the circumstances in which our proposed upper bounds might be tighter than other earlier upper bounds.

Supermodular f-divergences and bounds on lossy compression and generalization error with mutual f-information

In this paper, we introduce super-modular $\mf$-divergences and provide three applications for them: (i) we introduce Sanov's upper bound on the tail probability of sum of independent random variables based on super-modular $\mf$-divergence and show that our generalized Sanov's bound strictly improves over ordinary one, (ii) we consider the lossy compression problem which studies the set of achievable rates for a given distortion and code length. We extend the rate-distortion function using mutual $\mf$-information and provide new and strictly better bounds on achievable rates in the finite blocklength regime using super-modular $\mf$-divergences, and (iii) we provide a connection between the generalization error of algorithms with bounded input/output mutual $\mf$-information and a generalized rate-distortion problem. This connection allows us to bound the generalization error of learning algorithms using lower bounds on the rate-distortion function. Our bound is based on a new lower bound on the rate-distortion function that (for some examples) strictly improves over previously best-known bounds. Moreover, super-modular $\mf$-divergences are utilized to reduce the dimension of the problem and obtain single-letter bounds.

Stochastic Second-Order Methods Provably Beat SGD For Gradient-Dominated Functions

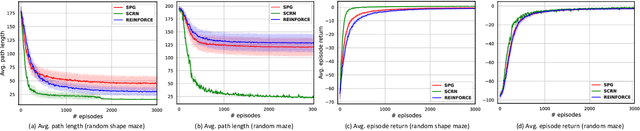
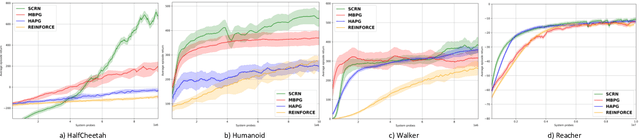
We study the performance of Stochastic Cubic Regularized Newton (SCRN) on a class of functions satisfying gradient dominance property which holds in a wide range of applications in machine learning and signal processing. This condition ensures that any first-order stationary point is a global optimum. We prove that SCRN improves the best-known sample complexity of stochastic gradient descent in achieving $\epsilon$-global optimum by a factor of $\mathcal{O}(\epsilon^{-1/2})$. Even under a weak version of gradient dominance property, which is applicable to policy-based reinforcement learning (RL), SCRN achieves the same improvement over stochastic policy gradient methods. Additionally, we show that the sample complexity of SCRN can be improved by a factor of ${\mathcal{O}}(\epsilon^{-1/2})$ using a variance reduction method with time-varying batch sizes. Experimental results in various RL settings showcase the remarkable performance of SCRN compared to first-order methods.