Seeing and Reasoning with Confidence: Supercharging Multimodal LLMs with an Uncertainty-Aware Agentic Framework

Multimodal large language models (MLLMs) show promise in tasks like visual question answering (VQA) but still face challenges in multimodal reasoning. Recent works adapt agentic frameworks or chain-of-thought (CoT) reasoning to improve performance. However, CoT-based multimodal reasoning often demands costly data annotation and fine-tuning, while agentic approaches relying on external tools risk introducing unreliable output from these tools. In this paper, we propose Seeing and Reasoning with Confidence (SRICE), a training-free multimodal reasoning framework that integrates external vision models with uncertainty quantification (UQ) into an MLLM to address these challenges. Specifically, SRICE guides the inference process by allowing MLLM to autonomously select regions of interest through multi-stage interactions with the help of external tools. We propose to use a conformal prediction-based approach to calibrate the output of external tools and select the optimal tool by estimating the uncertainty of an MLLM's output. Our experiment shows that the average improvement of SRICE over the base MLLM is 4.6% on five datasets and the performance on some datasets even outperforms fine-tuning-based methods, revealing the significance of ensuring reliable tool use in an MLLM agent.

Optimization Guarantees of Unfolded ISTA and ADMM Networks With Smooth Soft-Thresholding

Solving linear inverse problems plays a crucial role in numerous applications. Algorithm unfolding based, model-aware data-driven approaches have gained significant attention for effectively addressing these problems. Learned iterative soft-thresholding algorithm (LISTA) and alternating direction method of multipliers compressive sensing network (ADMM-CSNet) are two widely used such approaches, based on ISTA and ADMM algorithms, respectively. In this work, we study optimization guarantees, i.e., achieving near-zero training loss with the increase in the number of learning epochs, for finite-layer unfolded networks such as LISTA and ADMM-CSNet with smooth soft-thresholding in an over-parameterized (OP) regime. We achieve this by leveraging a modified version of the Polyak-Lojasiewicz, denoted PL$^*$, condition. Satisfying the PL$^*$ condition within a specific region of the loss landscape ensures the existence of a global minimum and exponential convergence from initialization using gradient descent based methods. Hence, we provide conditions, in terms of the network width and the number of training samples, on these unfolded networks for the PL$^*$ condition to hold. We achieve this by deriving the Hessian spectral norm of these networks. Additionally, we show that the threshold on the number of training samples increases with the increase in the network width. Furthermore, we compare the threshold on training samples of unfolded networks with that of a standard fully-connected feed-forward network (FFNN) with smooth soft-thresholding non-linearity. We prove that unfolded networks have a higher threshold value than FFNN. Consequently, one can expect a better expected error for unfolded networks than FFNN.

Generalization and Estimation Error Bounds for Model-based Neural Networks

Model-based neural networks provide unparalleled performance for various tasks, such as sparse coding and compressed sensing problems. Due to the strong connection with the sensing model, these networks are interpretable and inherit prior structure of the problem. In practice, model-based neural networks exhibit higher generalization capability compared to ReLU neural networks. However, this phenomenon was not addressed theoretically. Here, we leverage complexity measures including the global and local Rademacher complexities, in order to provide upper bounds on the generalization and estimation errors of model-based networks. We show that the generalization abilities of model-based networks for sparse recovery outperform those of regular ReLU networks, and derive practical design rules that allow to construct model-based networks with guaranteed high generalization. We demonstrate through a series of experiments that our theoretical insights shed light on a few behaviours experienced in practice, including the fact that ISTA and ADMM networks exhibit higher generalization abilities (especially for small number of training samples), compared to ReLU networks.

Learning Algorithm Generalization Error Bounds via Auxiliary Distributions

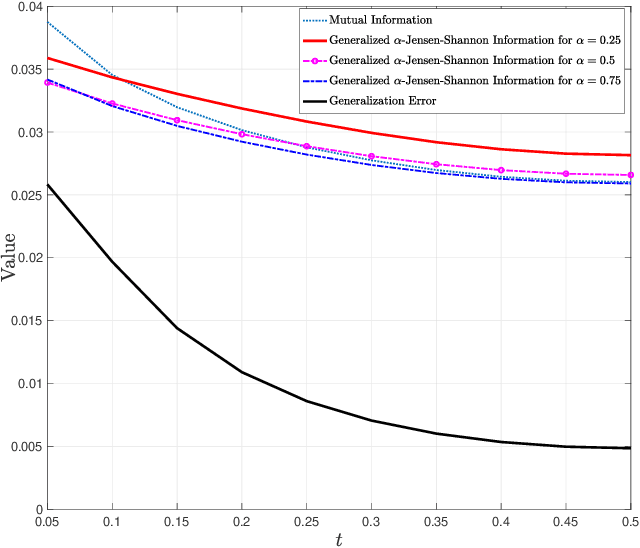
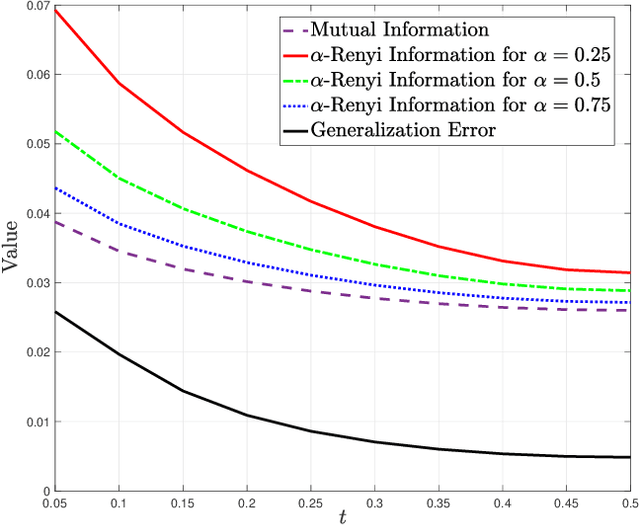
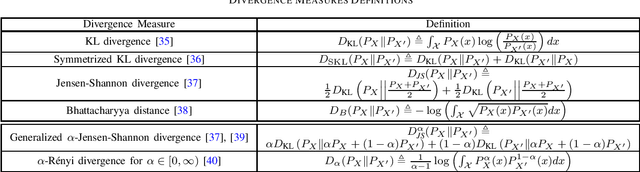
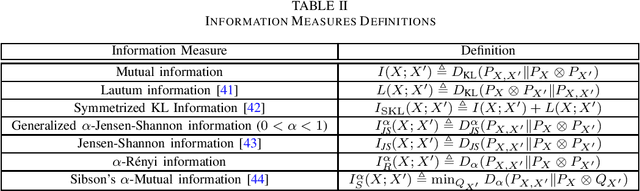
Generalization error boundaries are essential for comprehending how well machine learning models work. In this work, we suggest a creative method, i.e., the Auxiliary Distribution Method, that derives new upper bounds on generalization errors that are appropriate for supervised learning scenarios. We show that our general upper bounds can be specialized under some conditions to new bounds involving the generalized $\alpha$-Jensen-Shannon, $\alpha$-R\'enyi ($0< \alpha < 1$) information between random variable modeling the set of training samples and another random variable modeling the set of hypotheses. Our upper bounds based on generalized $\alpha$-Jensen-Shannon information are also finite. Additionally, we demonstrate how our auxiliary distribution method can be used to derive the upper bounds on generalization error under the distribution mismatch scenario in supervised learning algorithms, where the distributional mismatch is modeled as $\alpha$-Jensen-Shannon or $\alpha$-R\'enyi ($0< \alpha < 1$) between the distribution of test and training data samples. We also outline the circumstances in which our proposed upper bounds might be tighter than other earlier upper bounds.

Theoretical Perspectives on Deep Learning Methods in Inverse Problems

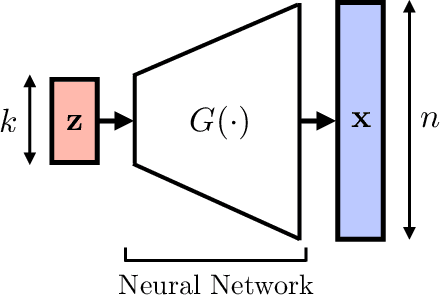
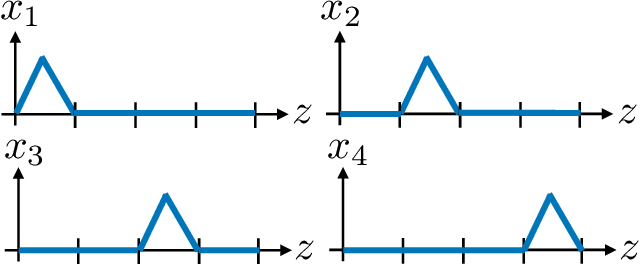
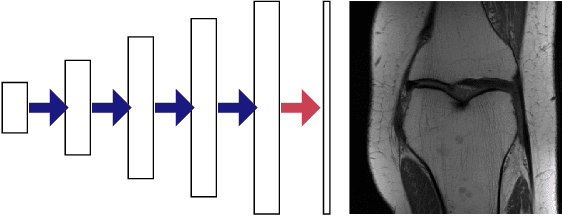
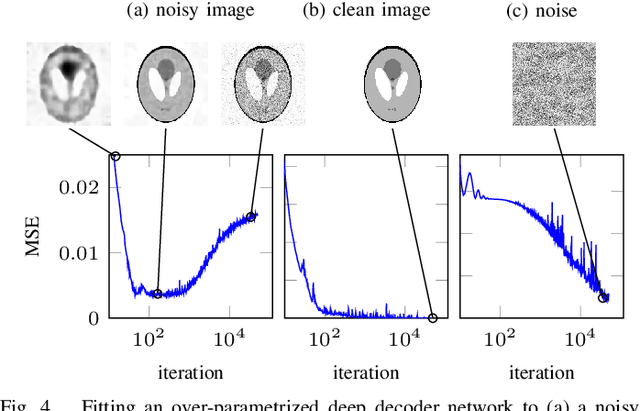
In recent years, there have been significant advances in the use of deep learning methods in inverse problems such as denoising, compressive sensing, inpainting, and super-resolution. While this line of works has predominantly been driven by practical algorithms and experiments, it has also given rise to a variety of intriguing theoretical problems. In this paper, we survey some of the prominent theoretical developments in this line of works, focusing in particular on generative priors, untrained neural network priors, and unfolding algorithms. In addition to summarizing existing results in these topics, we highlight several ongoing challenges and open problems.

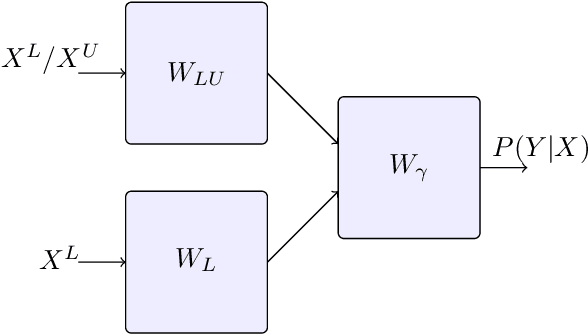
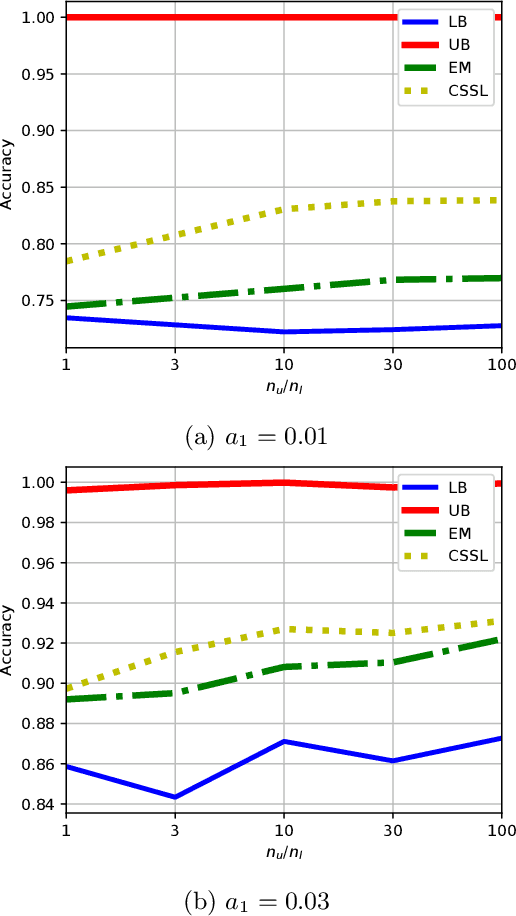
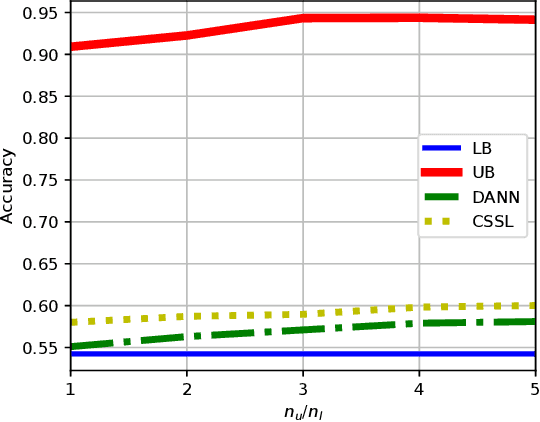
An Information-theoretical Approach to Semi-supervised Learning under Covariate-shift

A common assumption in semi-supervised learning is that the labeled, unlabeled, and test data are drawn from the same distribution. However, this assumption is not satisfied in many applications. In many scenarios, the data is collected sequentially (e.g., healthcare) and the distribution of the data may change over time often exhibiting so-called covariate shifts. In this paper, we propose an approach for semi-supervised learning algorithms that is capable of addressing this issue. Our framework also recovers some popular methods, including entropy minimization and pseudo-labeling. We provide new information-theoretical based generalization error upper bounds inspired by our novel framework. Our bounds are applicable to both general semi-supervised learning and the covariate-shift scenario. Finally, we show numerically that our method outperforms previous approaches proposed for semi-supervised learning under the covariate shift.

Robust lEarned Shrinkage-Thresholding (REST): Robust unrolling for sparse recover

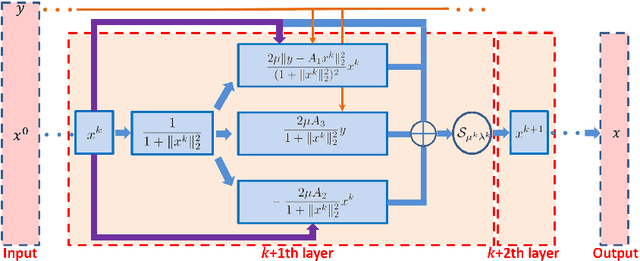
In this paper, we consider deep neural networks for solving inverse problems that are robust to forward model mis-specifications. Specifically, we treat sensing problems with model mismatch where one wishes to recover a sparse high-dimensional vector from low-dimensional observations subject to uncertainty in the measurement operator. We then design a new robust deep neural network architecture by applying algorithm unfolding techniques to a robust version of the underlying recovery problem. Our proposed network - named Robust lEarned Shrinkage-Thresholding (REST) - exhibits an additional normalization processing compared to Learned Iterative Shrinkage-Thresholding Algorithm (LISTA), leading to reliable recovery of the signal under sample-wise varying model mismatch. The proposed REST network is shown to outperform state-of-the-art model-based and data-driven algorithms in both compressive sensing and radar imaging problems wherein model mismatch is taken into consideration.

Characterizing the Generalization Error of Gibbs Algorithm with Symmetrized KL information

Bounding the generalization error of a supervised learning algorithm is one of the most important problems in learning theory, and various approaches have been developed. However, existing bounds are often loose and lack of guarantees. As a result, they may fail to characterize the exact generalization ability of a learning algorithm. Our main contribution is an exact characterization of the expected generalization error of the well-known Gibbs algorithm in terms of symmetrized KL information between the input training samples and the output hypothesis. Such a result can be applied to tighten existing expected generalization error bound. Our analysis provides more insight on the fundamental role the symmetrized KL information plays in controlling the generalization error of the Gibbs algorithm.

Information-Theoretic Bounds on the Moments of the Generalization Error of Learning Algorithms

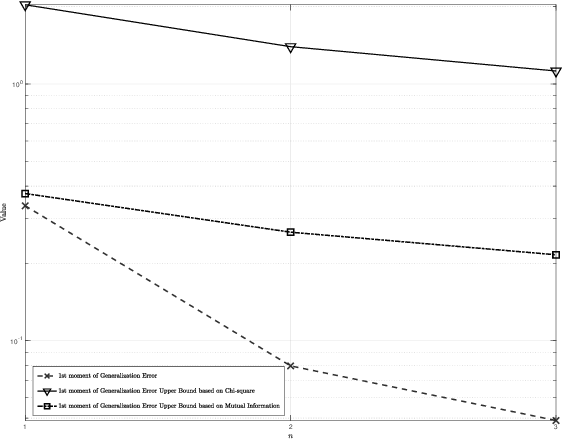
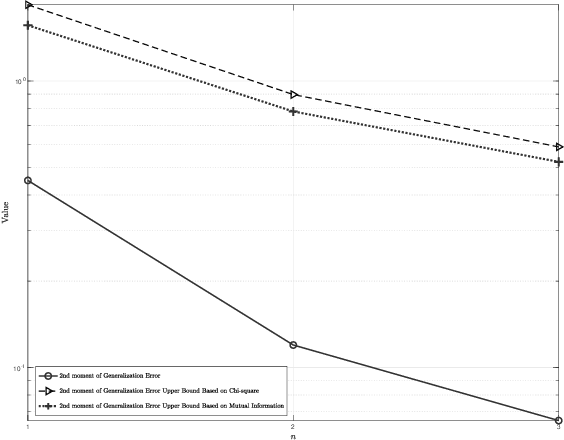
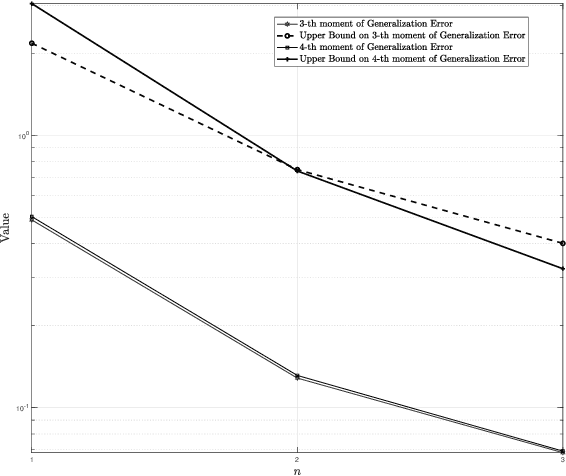
Generalization error bounds are critical to understanding the performance of machine learning models. In this work, building upon a new bound of the expected value of an arbitrary function of the population and empirical risk of a learning algorithm, we offer a more refined analysis of the generalization behaviour of a machine learning models based on a characterization of (bounds) to their generalization error moments. We discuss how the proposed bounds -- which also encompass new bounds to the expected generalization error -- relate to existing bounds in the literature. We also discuss how the proposed generalization error moment bounds can be used to construct new generalization error high-probability bounds.

Jensen-Shannon Information Based Characterization of the Generalization Error of Learning Algorithms

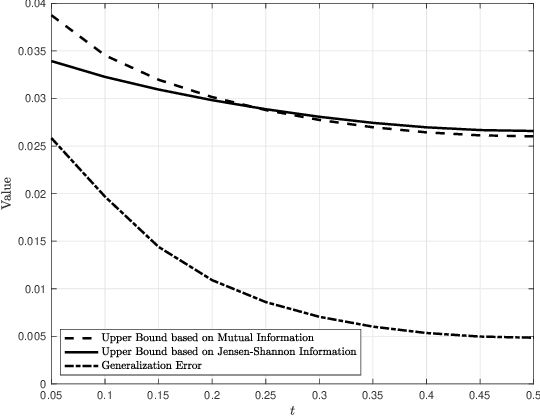
Generalization error bounds are critical to understanding the performance of machine learning models. In this work, we propose a new information-theoretic based generalization error upper bound applicable to supervised learning scenarios. We show that our general bound can specialize in various previous bounds. We also show that our general bound can be specialized under some conditions to a new bound involving the Jensen-Shannon information between a random variable modelling the set of training samples and another random variable modelling the set of hypotheses. We also prove that our bound can be tighter than mutual information-based bounds under some conditions.