Semi-Supervised Sparse Gaussian Classification: Provable Benefits of Unlabeled Data

The premise of semi-supervised learning (SSL) is that combining labeled and unlabeled data yields significantly more accurate models. Despite empirical successes, the theoretical understanding of SSL is still far from complete. In this work, we study SSL for high dimensional sparse Gaussian classification. To construct an accurate classifier a key task is feature selection, detecting the few variables that separate the two classes. % For this SSL setting, we analyze information theoretic lower bounds for accurate feature selection as well as computational lower bounds, assuming the low-degree likelihood hardness conjecture. % Our key contribution is the identification of a regime in the problem parameters (dimension, sparsity, number of labeled and unlabeled samples) where SSL is guaranteed to be advantageous for classification. Specifically, there is a regime where it is possible to construct in polynomial time an accurate SSL classifier. However, % any computationally efficient supervised or unsupervised learning schemes, that separately use only the labeled or unlabeled data would fail. Our work highlights the provable benefits of combining labeled and unlabeled data for {classification and} feature selection in high dimensions. We present simulations that complement our theoretical analysis.

Generalization and Estimation Error Bounds for Model-based Neural Networks

Model-based neural networks provide unparalleled performance for various tasks, such as sparse coding and compressed sensing problems. Due to the strong connection with the sensing model, these networks are interpretable and inherit prior structure of the problem. In practice, model-based neural networks exhibit higher generalization capability compared to ReLU neural networks. However, this phenomenon was not addressed theoretically. Here, we leverage complexity measures including the global and local Rademacher complexities, in order to provide upper bounds on the generalization and estimation errors of model-based networks. We show that the generalization abilities of model-based networks for sparse recovery outperform those of regular ReLU networks, and derive practical design rules that allow to construct model-based networks with guaranteed high generalization. We demonstrate through a series of experiments that our theoretical insights shed light on a few behaviours experienced in practice, including the fact that ISTA and ADMM networks exhibit higher generalization abilities (especially for small number of training samples), compared to ReLU networks.

Robust Unlimited Sampling Beyond Modulo

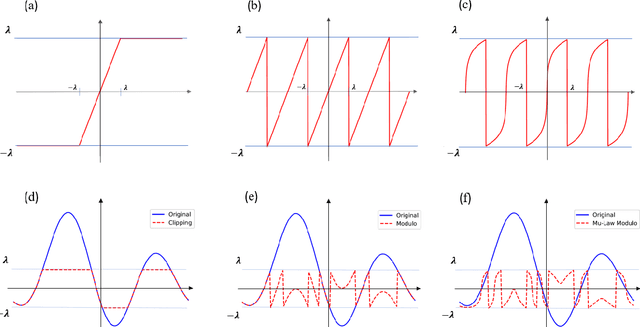
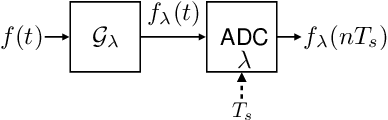
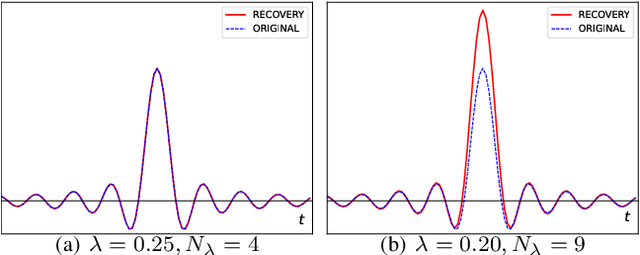
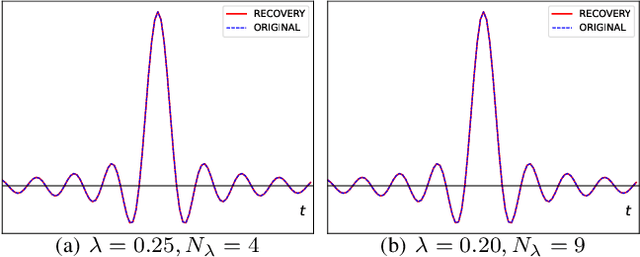
Analog to digital converters (ADCs) act as a bridge between the analog and digital domains. Two important attributes of any ADC are sampling rate and its dynamic range. For bandlimited signals, the sampling should be above the Nyquist rate. It is also desired that the signals' dynamic range should be within that of the ADC's; otherwise, the signal will be clipped. Nonlinear operators such as modulo or companding can be used prior to sampling to avoid clipping. To recover the true signal from the samples of the nonlinear operator, either high sampling rates are required or strict constraints on the nonlinear operations are imposed, both of which are not desirable in practice. In this paper, we propose a generalized flexible nonlinear operator which is sampling efficient. Moreover, by carefully choosing its parameters, clipping, modulo, and companding can be seen as special cases of it. We show that bandlimited signals are uniquely identified from the nonlinear samples of the proposed operator when sampled above the Nyquist rate. Furthermore, we propose a robust algorithm to recover the true signal from the nonlinear samples. We show that our algorithm has the lowest mean-squared error while recovering the signal for a given sampling rate, noise level, and dynamic range of the compared to existing algorithms. Our results lead to less constrained hardware design to address the dynamic range issues while operating at the lowest rate possible.

Residual Recovery Algorithm For Modulo Sampling

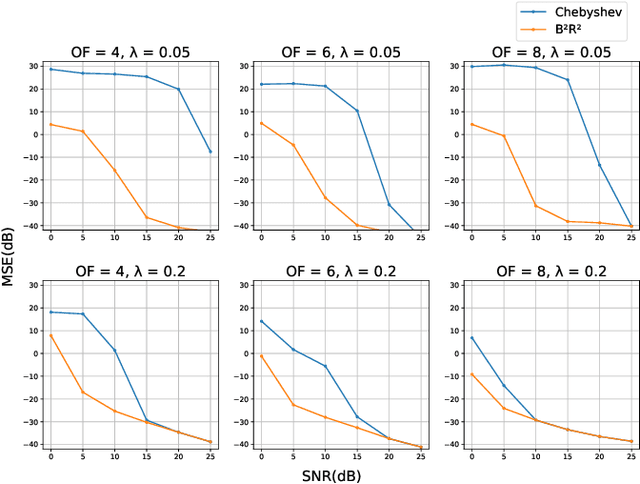
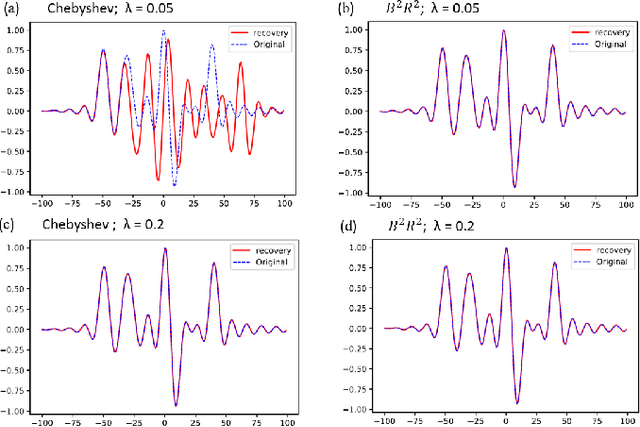
Two important attributes of analog to digital converters (ADCs) are its sampling rate and dynamic range. The sampling rate should be greater than or equal to the Nyquist rate for bandlimited signals with bounded energy. It is also desired that the signals' dynamic range should be within that of the ADC's; otherwise, the signal will be clipped. A modulo operator has been recently suggested prior to sampling to restrict the dynamic range. Due to the nonlinearity of the modulo operation, the samples are distorted. Existing recovery algorithms to recover the signal from its modulo samples operate at a high sampling rate and are not robust in the presence of noise. In this paper, we propose a robust algorithm to recover the signal from the modulo samples which operates at lower sampling rate compared to existing techniques. We also show that our method has lower error compared to existing approaches for a given sampling rate, noise level, and dynamic range of the ADC. Our results lead to less constrained hardware design to address dynamic range issues while operating at the lowest rate possible.