Robust Unlimited Sampling Beyond Modulo
Paper and Code
Jun 29, 2022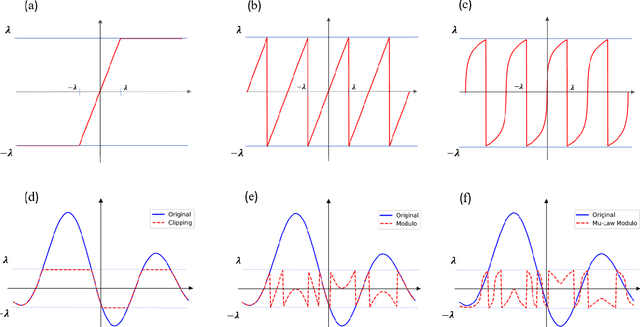
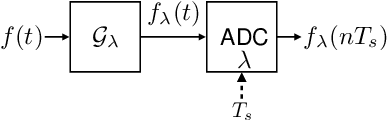
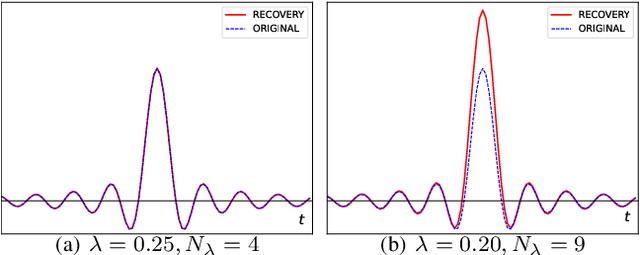
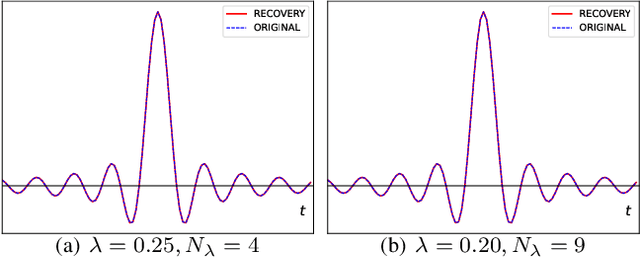
Analog to digital converters (ADCs) act as a bridge between the analog and digital domains. Two important attributes of any ADC are sampling rate and its dynamic range. For bandlimited signals, the sampling should be above the Nyquist rate. It is also desired that the signals' dynamic range should be within that of the ADC's; otherwise, the signal will be clipped. Nonlinear operators such as modulo or companding can be used prior to sampling to avoid clipping. To recover the true signal from the samples of the nonlinear operator, either high sampling rates are required or strict constraints on the nonlinear operations are imposed, both of which are not desirable in practice. In this paper, we propose a generalized flexible nonlinear operator which is sampling efficient. Moreover, by carefully choosing its parameters, clipping, modulo, and companding can be seen as special cases of it. We show that bandlimited signals are uniquely identified from the nonlinear samples of the proposed operator when sampled above the Nyquist rate. Furthermore, we propose a robust algorithm to recover the true signal from the nonlinear samples. We show that our algorithm has the lowest mean-squared error while recovering the signal for a given sampling rate, noise level, and dynamic range of the compared to existing algorithms. Our results lead to less constrained hardware design to address the dynamic range issues while operating at the lowest rate possible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge