GSRM: Generative Speech Reward Model for Speech RLHF

Recent advances in speech language models, such as GPT-4o Voice Mode and Gemini Live, have demonstrated promising speech generation capabilities. Nevertheless, the aesthetic naturalness of the synthesized audio still lags behind that of human speech. Enhancing generation quality requires a reliable evaluator of speech naturalness. However, existing naturalness evaluators typically regress raw audio to scalar scores, offering limited interpretability of the evaluation and moreover fail to generalize to speech across different taxonomies. Inspired by recent advances in generative reward modeling, we propose the Generative Speech Reward Model (GSRM), a reasoning-centric reward model tailored for speech. The GSRM is trained to decompose speech naturalness evaluation into an interpretable acoustic feature extraction stage followed by feature-grounded chain-of-thought reasoning, enabling explainable judgments. To achieve this, we curated a large-scale human feedback dataset comprising 31k expert ratings and an out-of-domain benchmark of real-world user-assistant speech interactions. Experiments show that GSRM substantially outperforms existing speech naturalness predictors, achieving model-human correlation of naturalness score prediction that approaches human inter-rater consistency. We further show how GSRM can improve the naturalness of speech LLM generations by serving as an effective verifier for online RLHF.

Satori-SWE: Evolutionary Test-Time Scaling for Sample-Efficient Software Engineering

Language models (LMs) perform well on standardized coding benchmarks but struggle with real-world software engineering tasks such as resolving GitHub issues in SWE-Bench, especially when model parameters are less than 100B. While smaller models are preferable in practice due to their lower computational cost, improving their performance remains challenging. Existing approaches primarily rely on supervised fine-tuning (SFT) with high-quality data, which is expensive to curate at scale. An alternative is test-time scaling: generating multiple outputs, scoring them using a verifier, and selecting the best one. Although effective, this strategy often requires excessive sampling and costly scoring, limiting its practical application. We propose Evolutionary Test-Time Scaling (EvoScale), a sample-efficient method that treats generation as an evolutionary process. By iteratively refining outputs via selection and mutation, EvoScale shifts the output distribution toward higher-scoring regions, reducing the number of samples needed to find correct solutions. To reduce the overhead from repeatedly sampling and selection, we train the model to self-evolve using reinforcement learning (RL). Rather than relying on external verifiers at inference time, the model learns to self-improve the scores of its own generations across iterations. Evaluated on SWE-Bench-Verified, EvoScale enables our 32B model, Satori-SWE-32B, to match or exceed the performance of models with over 100B parameters while using a few samples. Code, data, and models will be fully open-sourced.

Score-of-Mixture Training: Training One-Step Generative Models Made Simple

We propose Score-of-Mixture Training (SMT), a novel framework for training one-step generative models by minimizing a class of divergences called the $\alpha$-skew Jensen-Shannon divergence. At its core, SMT estimates the score of mixture distributions between real and fake samples across multiple noise levels. Similar to consistency models, our approach supports both training from scratch (SMT) and distillation using a pretrained diffusion model, which we call Score-of-Mixture Distillation (SMD). It is simple to implement, requires minimal hyperparameter tuning, and ensures stable training. Experiments on CIFAR-10 and ImageNet 64x64 show that SMT/SMD are competitive with and can even outperform existing methods.

Satori: Reinforcement Learning with Chain-of-Action-Thought Enhances LLM Reasoning via Autoregressive Search

Large language models (LLMs) have demonstrated remarkable reasoning capabilities across diverse domains. Recent studies have shown that increasing test-time computation enhances LLMs' reasoning capabilities. This typically involves extensive sampling at inference time guided by an external LLM verifier, resulting in a two-player system. Despite external guidance, the effectiveness of this system demonstrates the potential of a single LLM to tackle complex tasks. Thus, we pose a new research problem: Can we internalize the searching capabilities to fundamentally enhance the reasoning abilities of a single LLM? This work explores an orthogonal direction focusing on post-training LLMs for autoregressive searching (i.e., an extended reasoning process with self-reflection and self-exploration of new strategies). To achieve this, we propose the Chain-of-Action-Thought (COAT) reasoning and a two-stage training paradigm: 1) a small-scale format tuning stage to internalize the COAT reasoning format and 2) a large-scale self-improvement stage leveraging reinforcement learning. Our approach results in Satori, a 7B LLM trained on open-source models and data. Extensive empirical evaluations demonstrate that Satori achieves state-of-the-art performance on mathematical reasoning benchmarks while exhibits strong generalization to out-of-domain tasks. Code, data, and models will be fully open-sourced.

Reliable Gradient-free and Likelihood-free Prompt Tuning

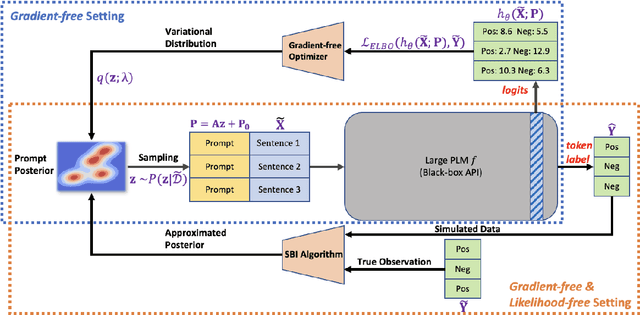
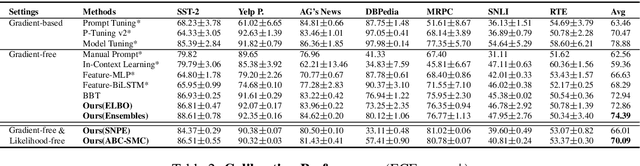
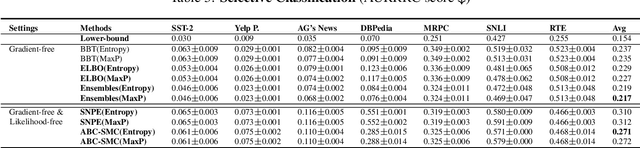
Due to privacy or commercial constraints, large pre-trained language models (PLMs) are often offered as black-box APIs. Fine-tuning such models to downstream tasks is challenging because one can neither access the model's internal representations nor propagate gradients through it. This paper addresses these challenges by developing techniques for adapting PLMs with only API access. Building on recent work on soft prompt tuning, we develop methods to tune the soft prompts without requiring gradient computation. Further, we develop extensions that in addition to not requiring gradients also do not need to access any internal representation of the PLM beyond the input embeddings. Moreover, instead of learning a single prompt, our methods learn a distribution over prompts allowing us to quantify predictive uncertainty. Ours is the first work to consider uncertainty in prompts when only having API access to the PLM. Finally, through extensive experiments, we carefully vet the proposed methods and find them competitive with (and sometimes even improving on) gradient-based approaches with full access to the PLM.

On the Generalization Error of Meta Learning for the Gibbs Algorithm

We analyze the generalization ability of joint-training meta learning algorithms via the Gibbs algorithm. Our exact characterization of the expected meta generalization error for the meta Gibbs algorithm is based on symmetrized KL information, which measures the dependence between all meta-training datasets and the output parameters, including task-specific and meta parameters. Additionally, we derive an exact characterization of the meta generalization error for the super-task Gibbs algorithm, in terms of conditional symmetrized KL information within the super-sample and super-task framework introduced in Steinke and Zakynthinou (2020) and Hellstrom and Durisi (2022) respectively. Our results also enable us to provide novel distribution-free generalization error upper bounds for these Gibbs algorithms applicable to meta learning.

Post-hoc Uncertainty Learning using a Dirichlet Meta-Model

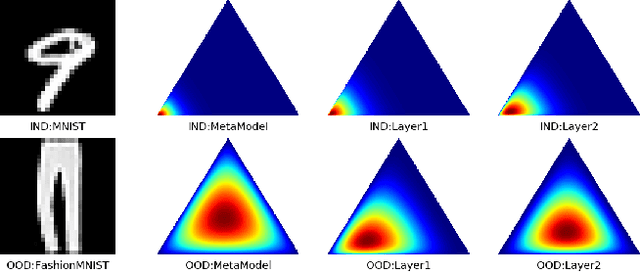
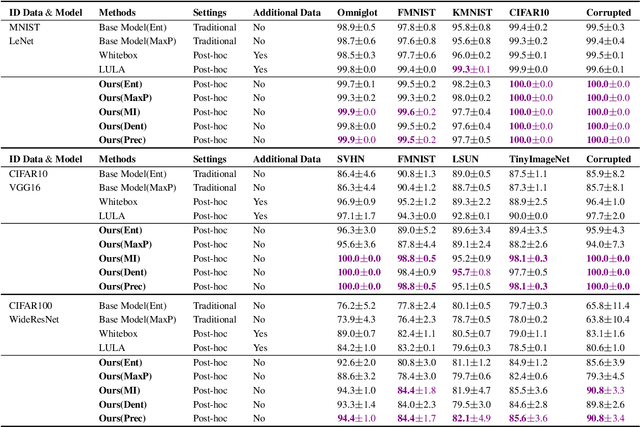
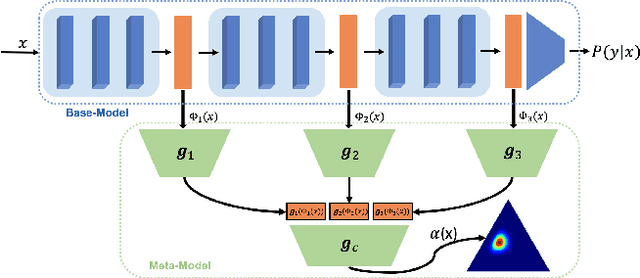
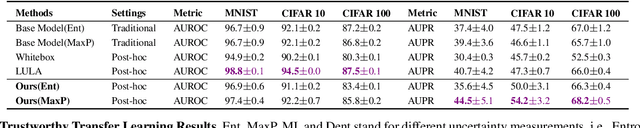
It is known that neural networks have the problem of being over-confident when directly using the output label distribution to generate uncertainty measures. Existing methods mainly resolve this issue by retraining the entire model to impose the uncertainty quantification capability so that the learned model can achieve desired performance in accuracy and uncertainty prediction simultaneously. However, training the model from scratch is computationally expensive and may not be feasible in many situations. In this work, we consider a more practical post-hoc uncertainty learning setting, where a well-trained base model is given, and we focus on the uncertainty quantification task at the second stage of training. We propose a novel Bayesian meta-model to augment pre-trained models with better uncertainty quantification abilities, which is effective and computationally efficient. Our proposed method requires no additional training data and is flexible enough to quantify different uncertainties and easily adapt to different application settings, including out-of-domain data detection, misclassification detection, and trustworthy transfer learning. We demonstrate our proposed meta-model approach's flexibility and superior empirical performance on these applications over multiple representative image classification benchmarks.

Tighter Expected Generalization Error Bounds via Convexity of Information Measures

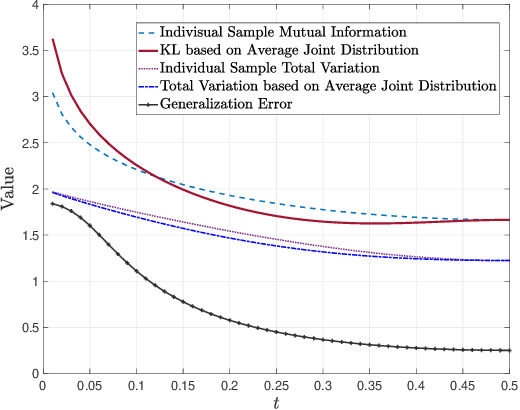
Generalization error bounds are essential to understanding machine learning algorithms. This paper presents novel expected generalization error upper bounds based on the average joint distribution between the output hypothesis and each input training sample. Multiple generalization error upper bounds based on different information measures are provided, including Wasserstein distance, total variation distance, KL divergence, and Jensen-Shannon divergence. Due to the convexity of the information measures, the proposed bounds in terms of Wasserstein distance and total variation distance are shown to be tighter than their counterparts based on individual samples in the literature. An example is provided to demonstrate the tightness of the proposed generalization error bounds.

On the Benefits of Selectivity in Pseudo-Labeling for Unsupervised Multi-Source-Free Domain Adaptation

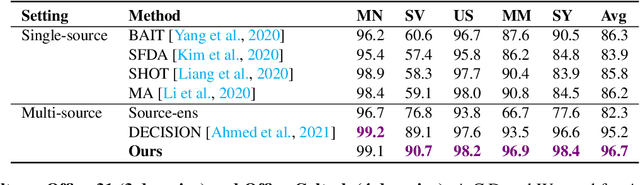
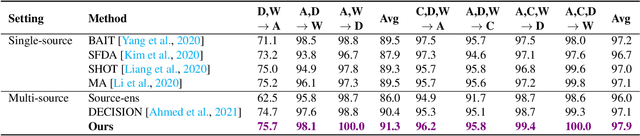
Due to privacy, storage, and other constraints, there is a growing need for unsupervised domain adaptation techniques in machine learning that do not require access to the data used to train a collection of source models. Existing methods for such multi-source-free domain adaptation typically train a target model using supervised techniques in conjunction with pseudo-labels for the target data, which are produced by the available source models. However, we show that assigning pseudo-labels to only a subset of the target data leads to improved performance. In particular, we develop an information-theoretic bound on the generalization error of the resulting target model that demonstrates an inherent bias-variance trade-off controlled by the subset choice. Guided by this analysis, we develop a method that partitions the target data into pseudo-labeled and unlabeled subsets to balance the trade-off. In addition to exploiting the pseudo-labeled subset, our algorithm further leverages the information in the unlabeled subset via a traditional unsupervised domain adaptation feature alignment procedure. Experiments on multiple benchmark datasets demonstrate the superior performance of the proposed method.

Characterizing and Understanding the Generalization Error of Transfer Learning with Gibbs Algorithm

We provide an information-theoretic analysis of the generalization ability of Gibbs-based transfer learning algorithms by focusing on two popular transfer learning approaches, $\alpha$-weighted-ERM and two-stage-ERM. Our key result is an exact characterization of the generalization behaviour using the conditional symmetrized KL information between the output hypothesis and the target training samples given the source samples. Our results can also be applied to provide novel distribution-free generalization error upper bounds on these two aforementioned Gibbs algorithms. Our approach is versatile, as it also characterizes the generalization errors and excess risks of these two Gibbs algorithms in the asymptotic regime, where they converge to the $\alpha$-weighted-ERM and two-stage-ERM, respectively. Based on our theoretical results, we show that the benefits of transfer learning can be viewed as a bias-variance trade-off, with the bias induced by the source distribution and the variance induced by the lack of target samples. We believe this viewpoint can guide the choice of transfer learning algorithms in practice.