Wave Physics-informed Matrix Factorizations

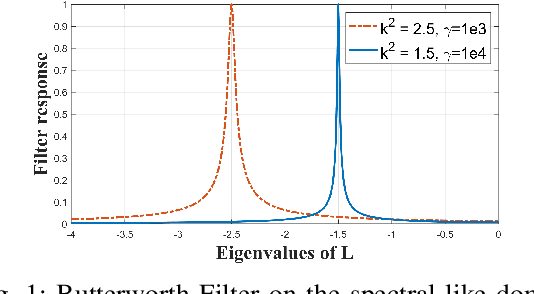
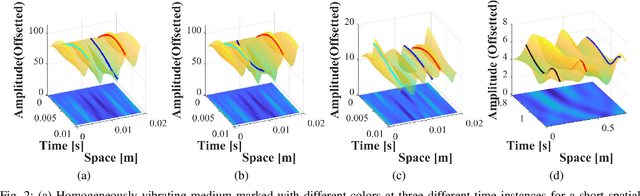
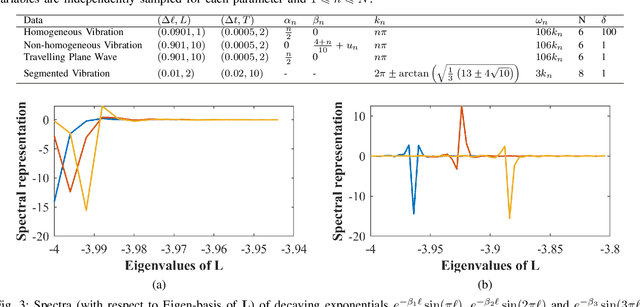
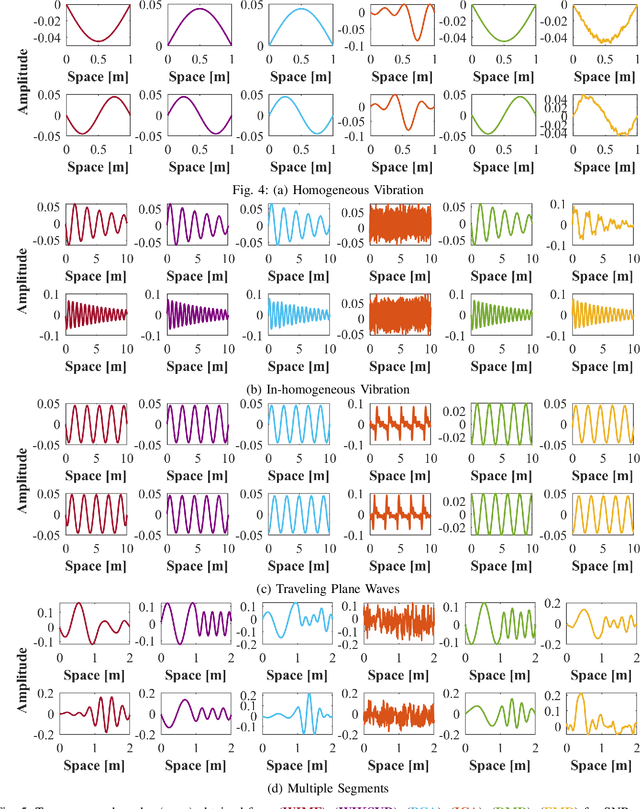
With the recent success of representation learning methods, which includes deep learning as a special case, there has been considerable interest in developing techniques that incorporate known physical constraints into the learned representation. As one example, in many applications that involve a signal propagating through physical media (e.g., optics, acoustics, fluid dynamics, etc), it is known that the dynamics of the signal must satisfy constraints imposed by the wave equation. Here we propose a matrix factorization technique that decomposes such signals into a sum of components, where each component is regularized to ensure that it {nearly} satisfies wave equation constraints. Although our proposed formulation is non-convex, we prove that our model can be efficiently solved to global optimality. Through this line of work we establish theoretical connections between wave-informed learning and filtering theory in signal processing. We further demonstrate the application of this work on modal analysis problems commonly arising in structural diagnostics and prognostics.

On the Generalization Error of Meta Learning for the Gibbs Algorithm

We analyze the generalization ability of joint-training meta learning algorithms via the Gibbs algorithm. Our exact characterization of the expected meta generalization error for the meta Gibbs algorithm is based on symmetrized KL information, which measures the dependence between all meta-training datasets and the output parameters, including task-specific and meta parameters. Additionally, we derive an exact characterization of the meta generalization error for the super-task Gibbs algorithm, in terms of conditional symmetrized KL information within the super-sample and super-task framework introduced in Steinke and Zakynthinou (2020) and Hellstrom and Durisi (2022) respectively. Our results also enable us to provide novel distribution-free generalization error upper bounds for these Gibbs algorithms applicable to meta learning.

Wave-Informed Matrix Factorization withGlobal Optimality Guarantees

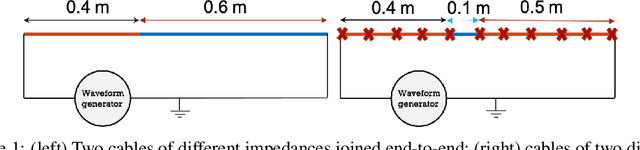
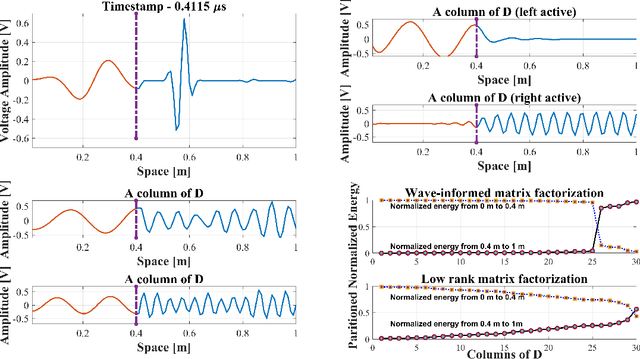
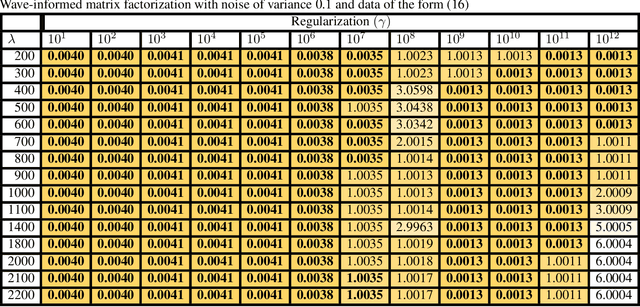
With the recent success of representation learning methods, which includes deep learning as a special case, there has been considerable interest in developing representation learning techniques that can incorporate known physical constraints into the learned representation. As one example, in many applications that involve a signal propagating through physical media (e.g., optics, acoustics, fluid dynamics, etc), it is known that the dynamics of the signal must satisfy constraints imposed by the wave equation. Here we propose a matrix factorization technique that decomposes such signals into a sum of components, where each component is regularized to ensure that it satisfies wave equation constraints. Although our proposed formulation is non-convex, we prove that our model can be efficiently solved to global optimality in polynomial time. We demonstrate the benefits of our work by applications in structural health monitoring, where prior work has attempted to solve this problem using sparse dictionary learning approaches that do not come with any theoretical guarantees regarding convergence to global optimality and employ heuristics to capture desired physical constraints.