Quantifying Heterogeneous Ecosystem Services With Multi-Label Soft Classification

Understanding and quantifying ecosystem services are crucial for sustainable environmental management, conservation efforts, and policy-making. The advancement of remote sensing technology and machine learning techniques has greatly facilitated this process. Yet, ground truth labels, such as biodiversity, are very difficult and expensive to measure. In addition, more easily obtainable proxy labels, such as land use, often fail to capture the complex heterogeneity of the ecosystem. In this paper, we demonstrate how land use proxy labels can be implemented with a soft, multi-label classifier to predict ecosystem services with complex heterogeneity.

Wave Physics-informed Matrix Factorizations

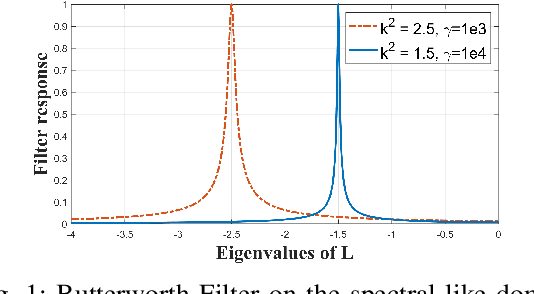
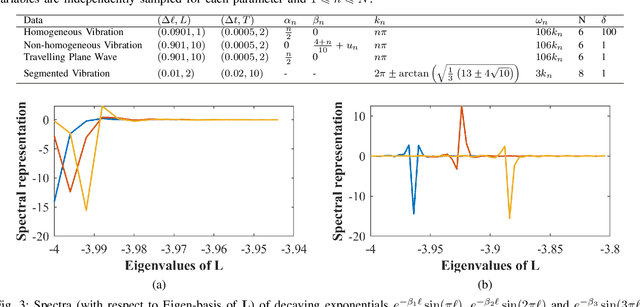
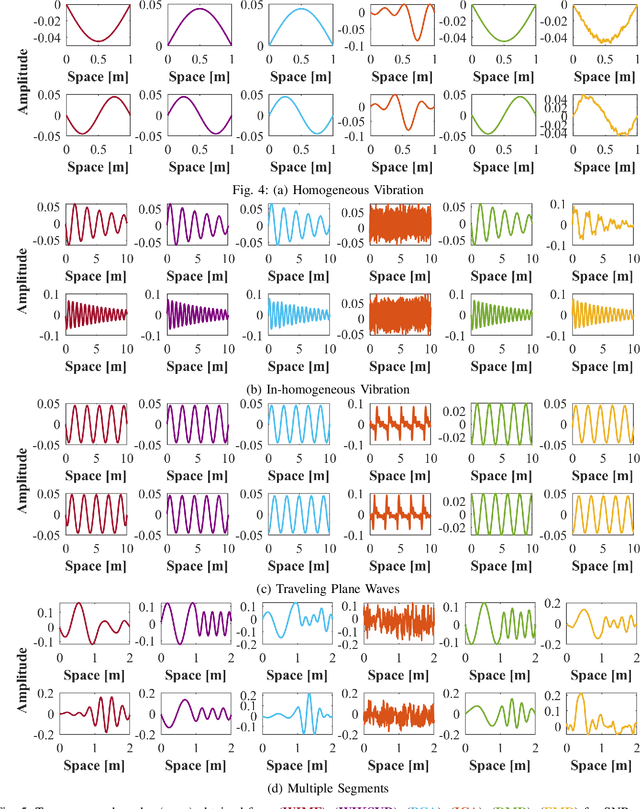
With the recent success of representation learning methods, which includes deep learning as a special case, there has been considerable interest in developing techniques that incorporate known physical constraints into the learned representation. As one example, in many applications that involve a signal propagating through physical media (e.g., optics, acoustics, fluid dynamics, etc), it is known that the dynamics of the signal must satisfy constraints imposed by the wave equation. Here we propose a matrix factorization technique that decomposes such signals into a sum of components, where each component is regularized to ensure that it {nearly} satisfies wave equation constraints. Although our proposed formulation is non-convex, we prove that our model can be efficiently solved to global optimality. Through this line of work we establish theoretical connections between wave-informed learning and filtering theory in signal processing. We further demonstrate the application of this work on modal analysis problems commonly arising in structural diagnostics and prognostics.

Modeling Fission Gas Release at the Mesoscale using Multiscale DenseNet Regression with Attention Mechanism and Inception Blocks

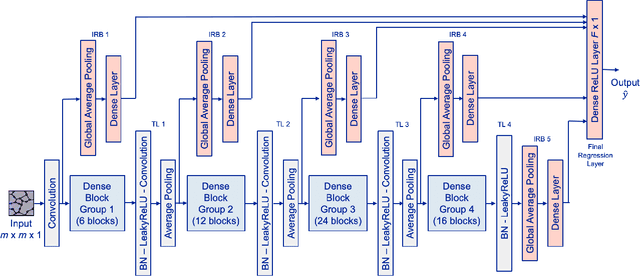
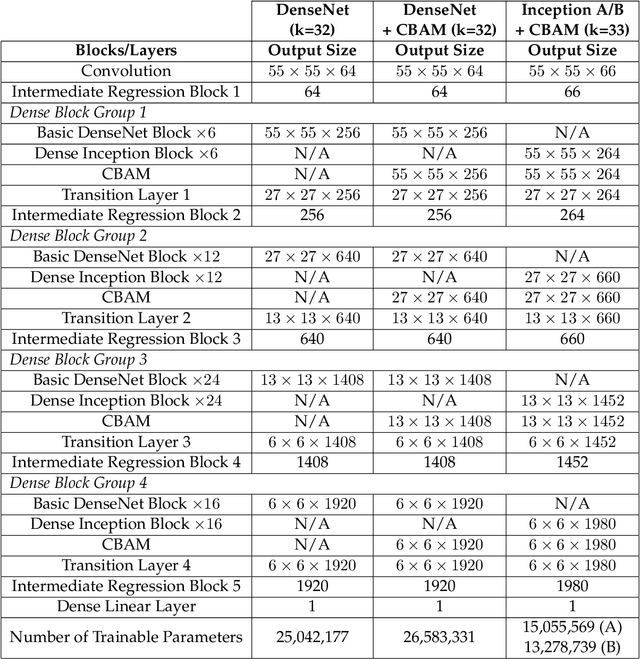
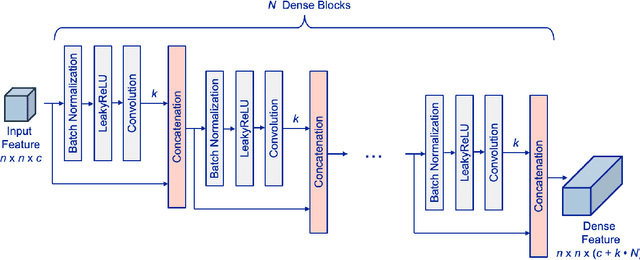
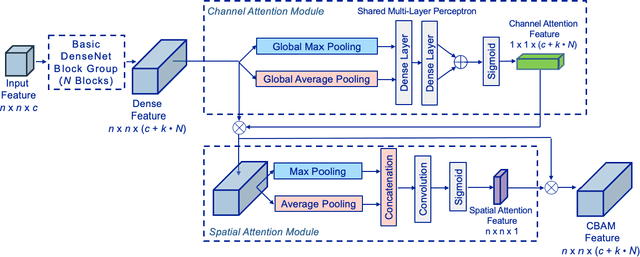
Mesoscale simulations of fission gas release (FGR) in nuclear fuel provide a powerful tool for understanding how microstructure evolution impacts FGR, but they are computationally intensive. In this study, we present an alternate, data-driven approach, using deep learning to predict instantaneous FGR flux from 2D nuclear fuel microstructure images. Four convolutional neural network (CNN) architectures with multiscale regression are trained and evaluated on simulated FGR data generated using a hybrid phase field/cluster dynamics model. All four networks show high predictive power, with $R^{2}$ values above 98%. The best performing network combine a Convolutional Block Attention Module (CBAM) and InceptionNet mechanisms to provide superior accuracy (mean absolute percentage error of 4.4%), training stability, and robustness on very low instantaneous FGR flux values.

Closing the sim-to-real gap in guided wave damage detection with adversarial training of variational auto-encoders

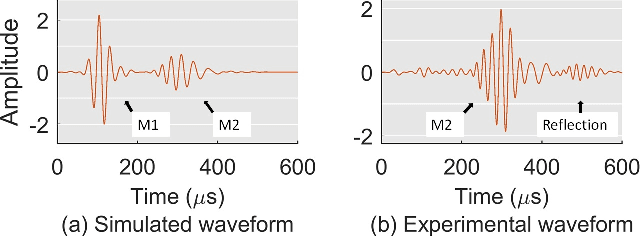
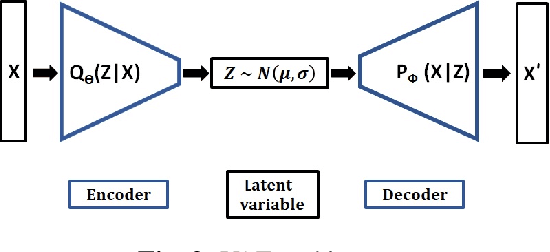
Guided wave testing is a popular approach for monitoring the structural integrity of infrastructures. We focus on the primary task of damage detection, where signal processing techniques are commonly employed. The detection performance is affected by a mismatch between the wave propagation model and experimental wave data. External variations, such as temperature, which are difficult to model, also affect the performance. While deep learning models can be an alternative detection method, there is often a lack of real-world training datasets. In this work, we counter this challenge by training an ensemble of variational autoencoders only on simulation data with a wave physics-guided adversarial component. We set up an experiment with non-uniform temperature variations to test the robustness of the methods. We compare our scheme with existing deep learning detection schemes and observe superior performance on experimental data.

Wave-Informed Matrix Factorization withGlobal Optimality Guarantees

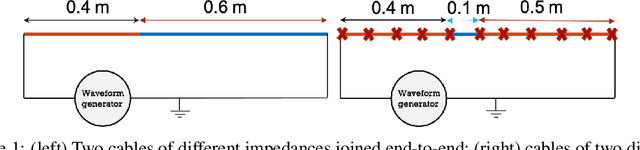
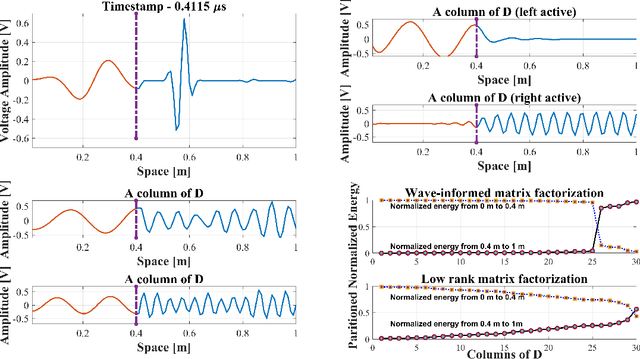
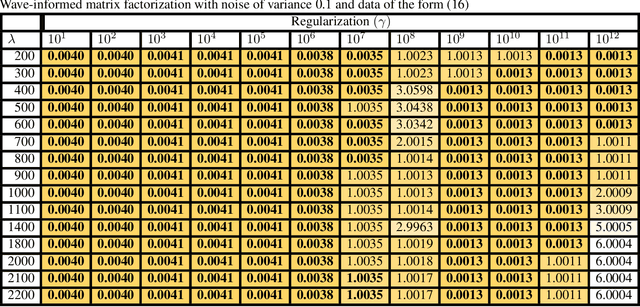
With the recent success of representation learning methods, which includes deep learning as a special case, there has been considerable interest in developing representation learning techniques that can incorporate known physical constraints into the learned representation. As one example, in many applications that involve a signal propagating through physical media (e.g., optics, acoustics, fluid dynamics, etc), it is known that the dynamics of the signal must satisfy constraints imposed by the wave equation. Here we propose a matrix factorization technique that decomposes such signals into a sum of components, where each component is regularized to ensure that it satisfies wave equation constraints. Although our proposed formulation is non-convex, we prove that our model can be efficiently solved to global optimality in polynomial time. We demonstrate the benefits of our work by applications in structural health monitoring, where prior work has attempted to solve this problem using sparse dictionary learning approaches that do not come with any theoretical guarantees regarding convergence to global optimality and employ heuristics to capture desired physical constraints.

Uncertainty Aware Deep Neural Network for Multistatic Localization with Application to Ultrasonic Structural Health Monitoring

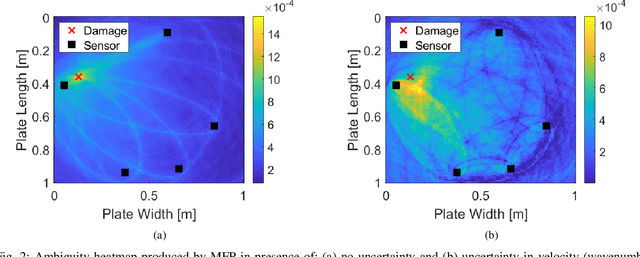
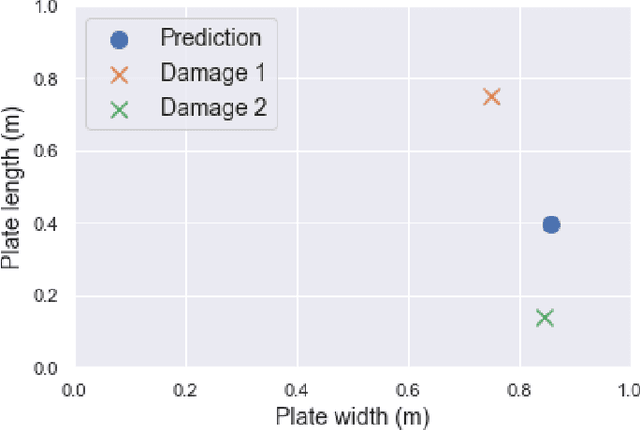
Guided ultrasonic wave localization uses spatially distributed multistatic sensor arrays and generalized beamforming strategies to detect and locate damage across a structure. The propagation channel is often very complex. Methods can compare data with models of wave propagation to locate damage. Yet, environmental uncertainty (e.g., temperature or stress variations) often degrade accuracies. This paper uses an uncertainty-aware deep neural network framework to learn robust localization models and represent uncertainty. We use mixture density networks to generate damage location distributions based on training data uncertainty. This is in contrast with most localization methods, which output point estimates. We compare our approach with matched field processing (MFP), a generalized beamforming framework. The proposed approach achieves a localization error of 0.0625 m as compared to 0.1425 m with MFP when data has environmental uncertainty and noise. We also show that the predictive uncertainty scales as environmental uncertainty increases to provide a statistically meaningful metric for assessing localization accuracy.

Accounting for Physics Uncertainty in Ultrasonic Wave Propagation using Deep Learning

Ultrasonic guided waves are commonly used to localize structural damage in infrastructures such as buildings, airplanes, bridges. Damage localization can be viewed as an inverse problem. Physical model based techniques are popular for guided wave based damage localization. The performance of these techniques depend on the degree of faithfulness with which the physical model describes wave propagation. External factors such as environmental variations and random noise are a source of uncertainty in wave propagation. The physical modeling of uncertainty in an inverse problem is still a challenging problem. In this work, we propose a deep learning based model for robust damage localization in presence of uncertainty. Wave data with uncertainty is simulated to reflect variations due to external factors and Gaussian noise is added to reflect random noise in the environment. After evaluating the localization error on test data with uncertainty, we observe that the deep learning model trained with uncertainty can learn robust representations. The approach shows potential for dealing with uncertainty in physical science problems using deep learning models.