Benjamin D. Haeffele
Nonconvex Linear System Identification with Minimal State Representation
Apr 26, 2025
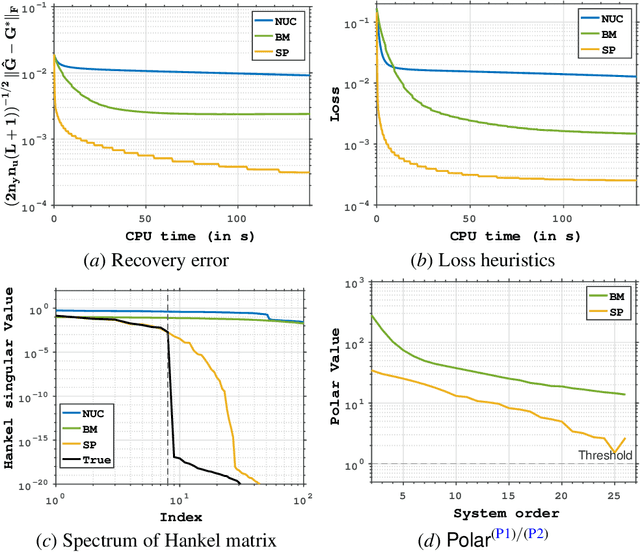
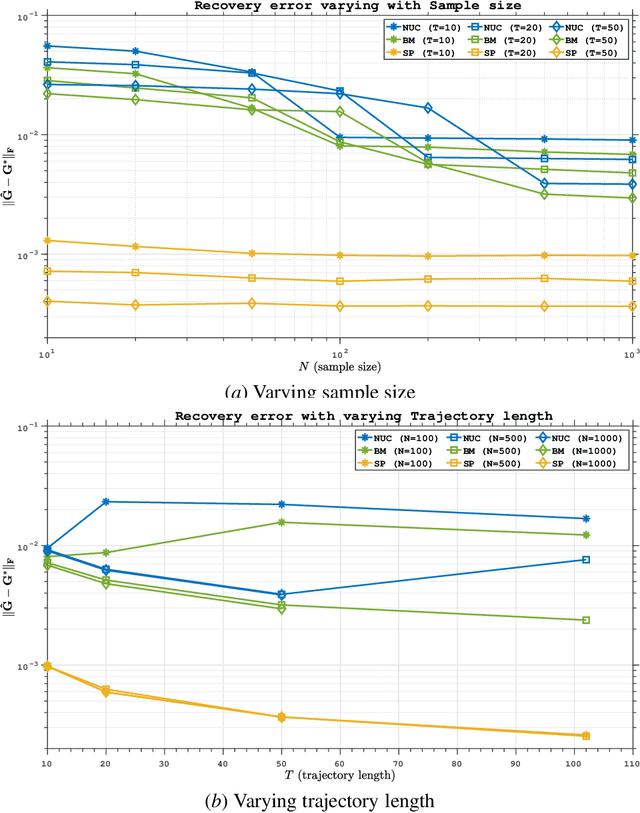
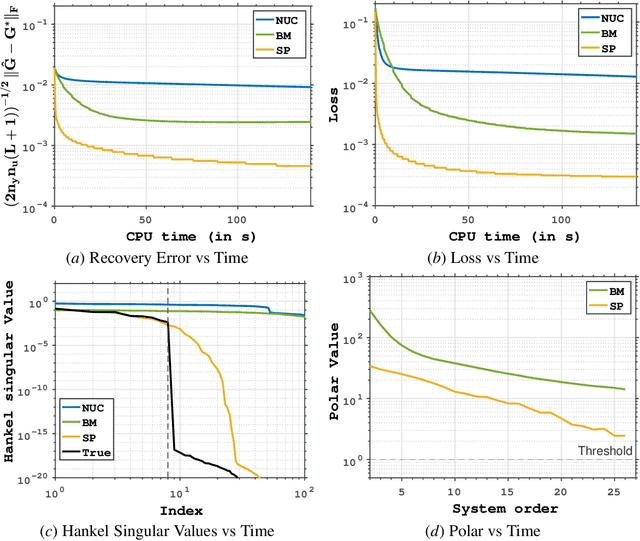
Abstract:Low-order linear System IDentification (SysID) addresses the challenge of estimating the parameters of a linear dynamical system from finite samples of observations and control inputs with minimal state representation. Traditional approaches often utilize Hankel-rank minimization, which relies on convex relaxations that can require numerous, costly singular value decompositions (SVDs) to optimize. In this work, we propose two nonconvex reformulations to tackle low-order SysID (i) Burer-Monterio (BM) factorization of the Hankel matrix for efficient nuclear norm minimization, and (ii) optimizing directly over system parameters for real, diagonalizable systems with an atomic norm style decomposition. These reformulations circumvent the need for repeated heavy SVD computations, significantly improving computational efficiency. Moreover, we prove that optimizing directly over the system parameters yields lower statistical error rates, and lower sample complexities that do not scale linearly with trajectory length like in Hankel-nuclear norm minimization. Additionally, while our proposed formulations are nonconvex, we provide theoretical guarantees of achieving global optimality in polynomial time. Finally, we demonstrate algorithms that solve these nonconvex programs and validate our theoretical claims on synthetic data.
An Overview of Low-Rank Structures in the Training and Adaptation of Large Models
Mar 25, 2025Abstract:The rise of deep learning has revolutionized data processing and prediction in signal processing and machine learning, yet the substantial computational demands of training and deploying modern large-scale deep models present significant challenges, including high computational costs and energy consumption. Recent research has uncovered a widespread phenomenon in deep networks: the emergence of low-rank structures in weight matrices and learned representations during training. These implicit low-dimensional patterns provide valuable insights for improving the efficiency of training and fine-tuning large-scale models. Practical techniques inspired by this phenomenon, such as low-rank adaptation (LoRA) and training, enable significant reductions in computational cost while preserving model performance. In this paper, we present a comprehensive review of recent advances in exploiting low-rank structures for deep learning and shed light on their mathematical foundations. Mathematically, we present two complementary perspectives on understanding the low-rankness in deep networks: (i) the emergence of low-rank structures throughout the whole optimization dynamics of gradient and (ii) the implicit regularization effects that induce such low-rank structures at convergence. From a practical standpoint, studying the low-rank learning dynamics of gradient descent offers a mathematical foundation for understanding the effectiveness of LoRA in fine-tuning large-scale models and inspires parameter-efficient low-rank training strategies. Furthermore, the implicit low-rank regularization effect helps explain the success of various masked training approaches in deep neural networks, ranging from dropout to masked self-supervised learning.
Token Statistics Transformer: Linear-Time Attention via Variational Rate Reduction
Dec 23, 2024



Abstract:The attention operator is arguably the key distinguishing factor of transformer architectures, which have demonstrated state-of-the-art performance on a variety of tasks. However, transformer attention operators often impose a significant computational burden, with the computational complexity scaling quadratically with the number of tokens. In this work, we propose a novel transformer attention operator whose computational complexity scales linearly with the number of tokens. We derive our network architecture by extending prior work which has shown that a transformer style architecture naturally arises by "white-box" architecture design, where each layer of the network is designed to implement an incremental optimization step of a maximal coding rate reduction objective (MCR$^2$). Specifically, we derive a novel variational form of the MCR$^2$ objective and show that the architecture that results from unrolled gradient descent of this variational objective leads to a new attention module called Token Statistics Self-Attention (TSSA). TSSA has linear computational and memory complexity and radically departs from the typical attention architecture that computes pairwise similarities between tokens. Experiments on vision, language, and long sequence tasks show that simply swapping TSSA for standard self-attention, which we refer to as the Token Statistics Transformer (ToST), achieves competitive performance with conventional transformers while being significantly more computationally efficient and interpretable. Our results also somewhat call into question the conventional wisdom that pairwise similarity style attention mechanisms are critical to the success of transformer architectures. Code will be available at https://github.com/RobinWu218/ToST.
A Convex Relaxation Approach to Generalization Analysis for Parallel Positively Homogeneous Networks
Nov 05, 2024
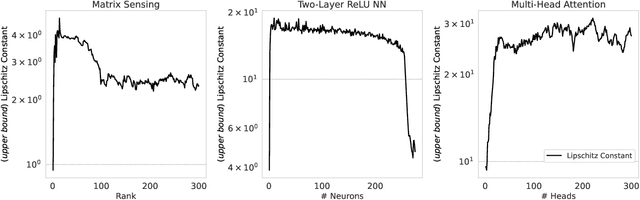
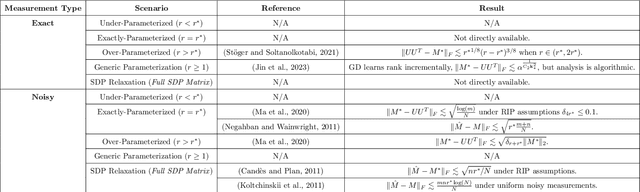
Abstract:We propose a general framework for deriving generalization bounds for parallel positively homogeneous neural networks--a class of neural networks whose input-output map decomposes as the sum of positively homogeneous maps. Examples of such networks include matrix factorization and sensing, single-layer multi-head attention mechanisms, tensor factorization, deep linear and ReLU networks, and more. Our general framework is based on linking the non-convex empirical risk minimization (ERM) problem to a closely related convex optimization problem over prediction functions, which provides a global, achievable lower-bound to the ERM problem. We exploit this convex lower-bound to perform generalization analysis in the convex space while controlling the discrepancy between the convex model and its non-convex counterpart. We apply our general framework to a wide variety of models ranging from low-rank matrix sensing, to structured matrix sensing, two-layer linear networks, two-layer ReLU networks, and single-layer multi-head attention mechanisms, achieving generalization bounds with a sample complexity that scales almost linearly with the network width.
Wave Physics-informed Matrix Factorizations
Dec 31, 2023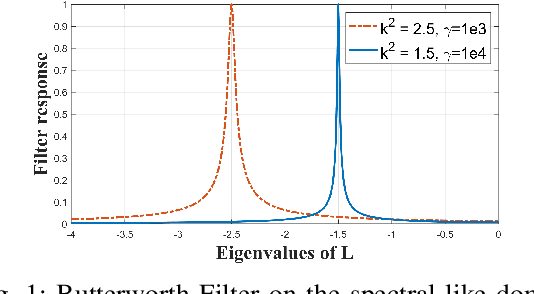
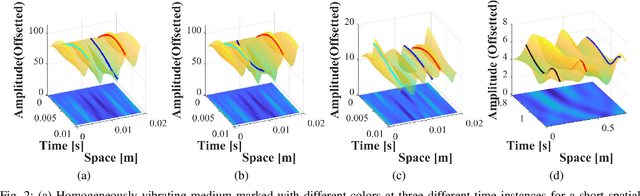
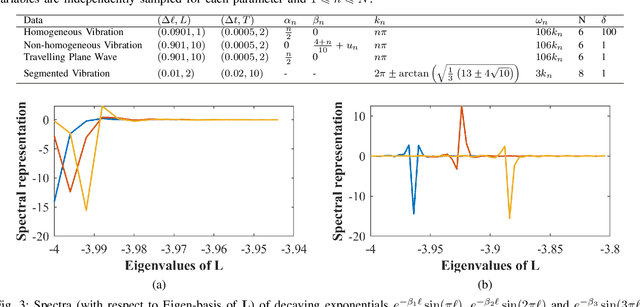
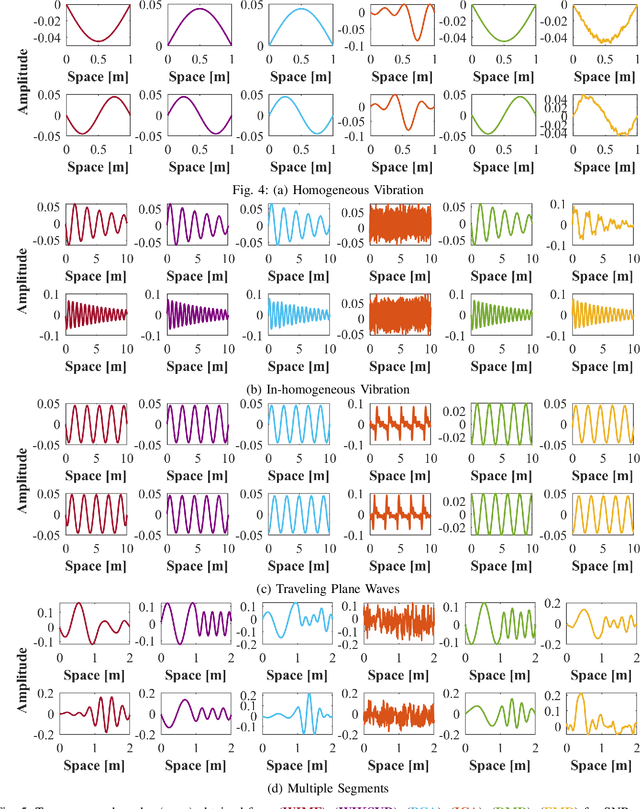
Abstract:With the recent success of representation learning methods, which includes deep learning as a special case, there has been considerable interest in developing techniques that incorporate known physical constraints into the learned representation. As one example, in many applications that involve a signal propagating through physical media (e.g., optics, acoustics, fluid dynamics, etc), it is known that the dynamics of the signal must satisfy constraints imposed by the wave equation. Here we propose a matrix factorization technique that decomposes such signals into a sum of components, where each component is regularized to ensure that it {nearly} satisfies wave equation constraints. Although our proposed formulation is non-convex, we prove that our model can be efficiently solved to global optimality. Through this line of work we establish theoretical connections between wave-informed learning and filtering theory in signal processing. We further demonstrate the application of this work on modal analysis problems commonly arising in structural diagnostics and prognostics.
White-Box Transformers via Sparse Rate Reduction: Compression Is All There Is?
Nov 24, 2023



Abstract:In this paper, we contend that a natural objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a low-dimensional Gaussian mixture supported on incoherent subspaces. The goodness of such a representation can be evaluated by a principled measure, called sparse rate reduction, that simultaneously maximizes the intrinsic information gain and extrinsic sparsity of the learned representation. From this perspective, popular deep network architectures, including transformers, can be viewed as realizing iterative schemes to optimize this measure. Particularly, we derive a transformer block from alternating optimization on parts of this objective: the multi-head self-attention operator compresses the representation by implementing an approximate gradient descent step on the coding rate of the features, and the subsequent multi-layer perceptron sparsifies the features. This leads to a family of white-box transformer-like deep network architectures, named CRATE, which are mathematically fully interpretable. We show, by way of a novel connection between denoising and compression, that the inverse to the aforementioned compressive encoding can be realized by the same class of CRATE architectures. Thus, the so-derived white-box architectures are universal to both encoders and decoders. Experiments show that these networks, despite their simplicity, indeed learn to compress and sparsify representations of large-scale real-world image and text datasets, and achieve performance very close to highly engineered transformer-based models: ViT, MAE, DINO, BERT, and GPT2. We believe the proposed computational framework demonstrates great potential in bridging the gap between theory and practice of deep learning, from a unified perspective of data compression. Code is available at: https://ma-lab-berkeley.github.io/CRATE .
White-Box Transformers via Sparse Rate Reduction
Jun 01, 2023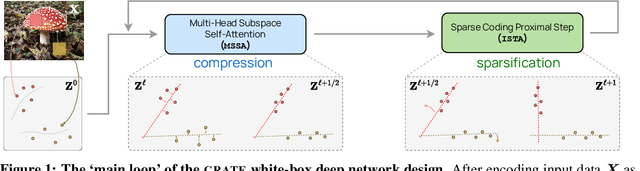
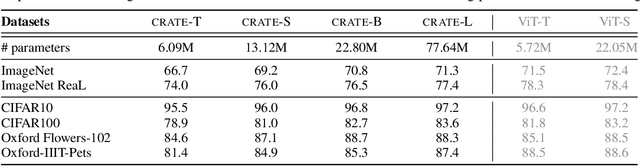
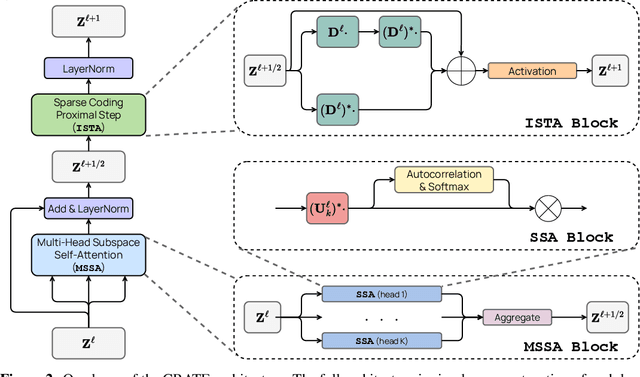
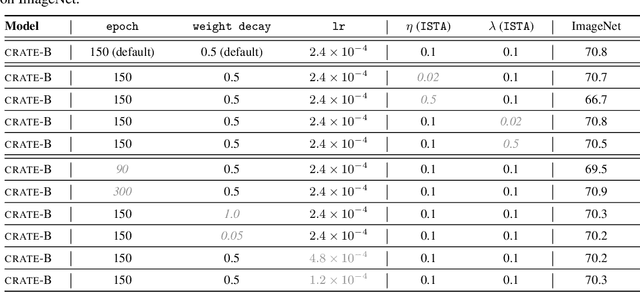
Abstract:In this paper, we contend that the objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a mixture of low-dimensional Gaussian distributions supported on incoherent subspaces. The quality of the final representation can be measured by a unified objective function called sparse rate reduction. From this perspective, popular deep networks such as transformers can be naturally viewed as realizing iterative schemes to optimize this objective incrementally. Particularly, we show that the standard transformer block can be derived from alternating optimization on complementary parts of this objective: the multi-head self-attention operator can be viewed as a gradient descent step to compress the token sets by minimizing their lossy coding rate, and the subsequent multi-layer perceptron can be viewed as attempting to sparsify the representation of the tokens. This leads to a family of white-box transformer-like deep network architectures which are mathematically fully interpretable. Despite their simplicity, experiments show that these networks indeed learn to optimize the designed objective: they compress and sparsify representations of large-scale real-world vision datasets such as ImageNet, and achieve performance very close to thoroughly engineered transformers such as ViT. Code is at \url{https://github.com/Ma-Lab-Berkeley/CRATE}.
Variational Information Pursuit for Interpretable Predictions
Feb 16, 2023Abstract:There is a growing interest in the machine learning community in developing predictive algorithms that are "interpretable by design". Towards this end, recent work proposes to make interpretable decisions by sequentially asking interpretable queries about data until a prediction can be made with high confidence based on the answers obtained (the history). To promote short query-answer chains, a greedy procedure called Information Pursuit (IP) is used, which adaptively chooses queries in order of information gain. Generative models are employed to learn the distribution of query-answers and labels, which is in turn used to estimate the most informative query. However, learning and inference with a full generative model of the data is often intractable for complex tasks. In this work, we propose Variational Information Pursuit (V-IP), a variational characterization of IP which bypasses the need for learning generative models. V-IP is based on finding a query selection strategy and a classifier that minimizes the expected cross-entropy between true and predicted labels. We then demonstrate that the IP strategy is the optimal solution to this problem. Therefore, instead of learning generative models, we can use our optimal strategy to directly pick the most informative query given any history. We then develop a practical algorithm by defining a finite-dimensional parameterization of our strategy and classifier using deep networks and train them end-to-end using our objective. Empirically, V-IP is 10-100x faster than IP on different Vision and NLP tasks with competitive performance. Moreover, V-IP finds much shorter query chains when compared to reinforcement learning which is typically used in sequential-decision-making problems. Finally, we demonstrate the utility of V-IP on challenging tasks like medical diagnosis where the performance is far superior to the generative modelling approach.
Unsupervised Manifold Linearizing and Clustering
Jan 04, 2023Abstract:Clustering data lying close to a union of low-dimensional manifolds, with each manifold as a cluster, is a fundamental problem in machine learning. When the manifolds are assumed to be linear subspaces, many methods succeed using low-rank and sparse priors, which have been studied extensively over the past two decades. Unfortunately, most real-world datasets can not be well approximated by linear subspaces. On the other hand, several works have proposed to identify the manifolds by learning a feature map such that the data transformed by the map lie in a union of linear subspaces, even though the original data are from non-linear manifolds. However, most works either assume knowledge of the membership of samples to clusters, or are shown to learn trivial representations. In this paper, we propose to simultaneously perform clustering and learn a union-of-subspace representation via Maximal Coding Rate Reduction. Experiments on synthetic and realistic datasets show that the proposed method achieves clustering accuracy comparable with state-of-the-art alternatives, while being more scalable and learning geometrically meaningful representations.
Learning Globally Smooth Functions on Manifolds
Oct 01, 2022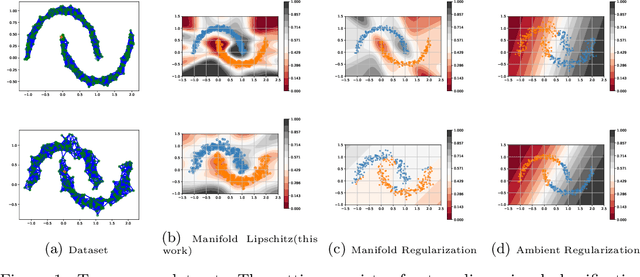

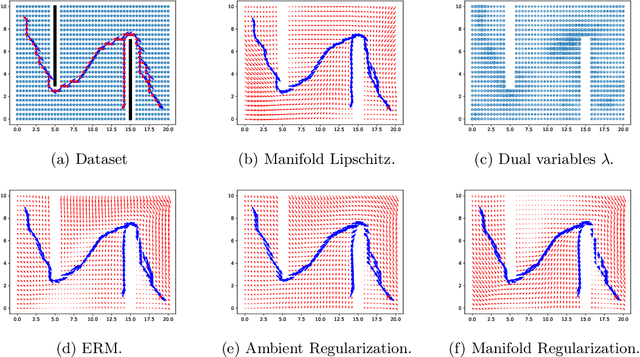

Abstract:Smoothness and low dimensional structures play central roles in improving generalization and stability in learning and statistics. The combination of these properties has led to many advances in semi-supervised learning, generative modeling, and control of dynamical systems. However, learning smooth functions is generally challenging, except in simple cases such as learning linear or kernel models. Typical methods are either too conservative, relying on crude upper bounds such as spectral normalization, too lax, penalizing smoothness on average, or too computationally intensive, requiring the solution of large-scale semi-definite programs. These issues are only exacerbated when trying to simultaneously exploit low dimensionality using, e.g., manifolds. This work proposes to overcome these obstacles by combining techniques from semi-infinite constrained learning and manifold regularization. To do so, it shows that, under typical conditions, the problem of learning a Lipschitz continuous function on a manifold is equivalent to a dynamically weighted manifold regularization problem. This observation leads to a practical algorithm based on a weighted Laplacian penalty whose weights are adapted using stochastic gradient techniques. We prove that, under mild conditions, this method estimates the Lipschitz constant of the solution, learning a globally smooth solution as a byproduct. Numerical examples illustrate the advantages of using this method to impose global smoothness on manifolds as opposed to imposing smoothness on average.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge