Juan Cervino
Generalization of Geometric Graph Neural Networks
Sep 08, 2024Abstract:In this paper, we study the generalization capabilities of geometric graph neural networks (GNNs). We consider GNNs over a geometric graph constructed from a finite set of randomly sampled points over an embedded manifold with topological information captured. We prove a generalization gap between the optimal empirical risk and the optimal statistical risk of this GNN, which decreases with the number of sampled points from the manifold and increases with the dimension of the underlying manifold. This generalization gap ensures that the GNN trained on a graph on a set of sampled points can be utilized to process other unseen graphs constructed from the same underlying manifold. The most important observation is that the generalization capability can be realized with one large graph instead of being limited to the size of the graph as in previous results. The generalization gap is derived based on the non-asymptotic convergence result of a GNN on the sampled graph to the underlying manifold neural networks (MNNs). We verify this theoretical result with experiments on both Arxiv dataset and Cora dataset.
Generalization of Graph Neural Networks is Robust to Model Mismatch
Aug 25, 2024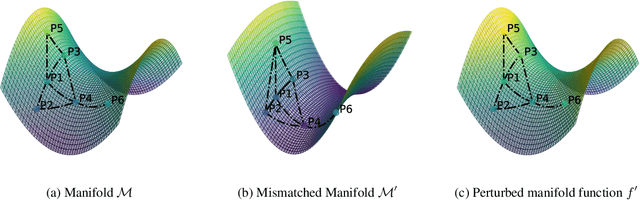
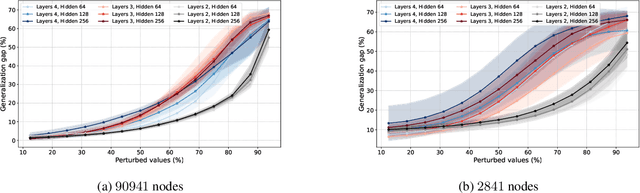
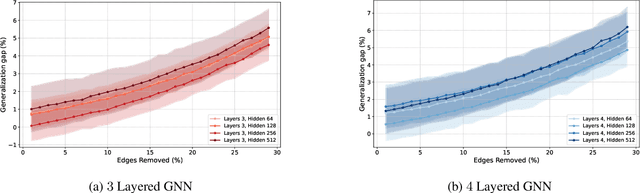
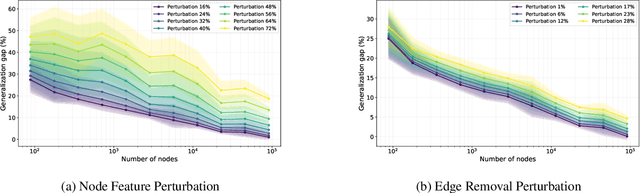
Abstract:Graph neural networks (GNNs) have demonstrated their effectiveness in various tasks supported by their generalization capabilities. However, the current analysis of GNN generalization relies on the assumption that training and testing data are independent and identically distributed (i.i.d). This imposes limitations on the cases where a model mismatch exists when generating testing data. In this paper, we examine GNNs that operate on geometric graphs generated from manifold models, explicitly focusing on scenarios where there is a mismatch between manifold models generating training and testing data. Our analysis reveals the robustness of the GNN generalization in the presence of such model mismatch. This indicates that GNNs trained on graphs generated from a manifold can still generalize well to unseen nodes and graphs generated from a mismatched manifold. We attribute this mismatch to both node feature perturbations and edge perturbations within the generated graph. Our findings indicate that the generalization gap decreases as the number of nodes grows in the training graph while increasing with larger manifold dimension as well as larger mismatch. Importantly, we observe a trade-off between the generalization of GNNs and the capability to discriminate high-frequency components when facing a model mismatch. The most important practical consequence of this analysis is to shed light on the filter design of generalizable GNNs robust to model mismatch. We verify our theoretical findings with experiments on multiple real-world datasets.
Distributed Training of Large Graph Neural Networks with Variable Communication Rates
Jun 25, 2024Abstract:Training Graph Neural Networks (GNNs) on large graphs presents unique challenges due to the large memory and computing requirements. Distributed GNN training, where the graph is partitioned across multiple machines, is a common approach to training GNNs on large graphs. However, as the graph cannot generally be decomposed into small non-interacting components, data communication between the training machines quickly limits training speeds. Compressing the communicated node activations by a fixed amount improves the training speeds, but lowers the accuracy of the trained GNN. In this paper, we introduce a variable compression scheme for reducing the communication volume in distributed GNN training without compromising the accuracy of the learned model. Based on our theoretical analysis, we derive a variable compression method that converges to a solution equivalent to the full communication case, for all graph partitioning schemes. Our empirical results show that our method attains a comparable performance to the one obtained with full communication. We outperform full communication at any fixed compression ratio for any communication budget.
A Manifold Perspective on the Statistical Generalization of Graph Neural Networks
Jun 07, 2024Abstract:Convolutional neural networks have been successfully extended to operate on graphs, giving rise to Graph Neural Networks (GNNs). GNNs combine information from adjacent nodes by successive applications of graph convolutions. GNNs have been implemented successfully in various learning tasks while the theoretical understanding of their generalization capability is still in progress. In this paper, we leverage manifold theory to analyze the statistical generalization gap of GNNs operating on graphs constructed on sampled points from manifolds. We study the generalization gaps of GNNs on both node-level and graph-level tasks. We show that the generalization gaps decrease with the number of nodes in the training graphs, which guarantees the generalization of GNNs to unseen points over manifolds. We validate our theoretical results in multiple real-world datasets.
Intrinsically motivated graph exploration using network theories of human curiosity
Jul 13, 2023



Abstract:Intrinsically motivated exploration has proven useful for reinforcement learning, even without additional extrinsic rewards. When the environment is naturally represented as a graph, how to guide exploration best remains an open question. In this work, we propose a novel approach for exploring graph-structured data motivated by two theories of human curiosity: the information gap theory and the compression progress theory. The theories view curiosity as an intrinsic motivation to optimize for topological features of subgraphs induced by the visited nodes in the environment. We use these proposed features as rewards for graph neural-network-based reinforcement learning. On multiple classes of synthetically generated graphs, we find that trained agents generalize to larger environments and to longer exploratory walks than are seen during training. Our method computes more efficiently than the greedy evaluation of the relevant topological properties. The proposed intrinsic motivations bear particular relevance for recommender systems. We demonstrate that curiosity-based recommendations are more predictive of human behavior than PageRank centrality for several real-world graph datasets, including MovieLens, Amazon Books, and Wikispeedia.
Multi-task Bias-Variance Trade-off Through Functional Constraints
Oct 27, 2022


Abstract:Multi-task learning aims to acquire a set of functions, either regressors or classifiers, that perform well for diverse tasks. At its core, the idea behind multi-task learning is to exploit the intrinsic similarity across data sources to aid in the learning process for each individual domain. In this paper we draw intuition from the two extreme learning scenarios -- a single function for all tasks, and a task-specific function that ignores the other tasks dependencies -- to propose a bias-variance trade-off. To control the relationship between the variance (given by the number of i.i.d. samples), and the bias (coming from data from other task), we introduce a constrained learning formulation that enforces domain specific solutions to be close to a central function. This problem is solved in the dual domain, for which we propose a stochastic primal-dual algorithm. Experimental results for a multi-domain classification problem with real data show that the proposed procedure outperforms both the task specific, as well as the single classifiers.
Training Graph Neural Networks on Growing Stochastic Graphs
Oct 27, 2022
Abstract:Graph Neural Networks (GNNs) rely on graph convolutions to exploit meaningful patterns in networked data. Based on matrix multiplications, convolutions incur in high computational costs leading to scalability limitations in practice. To overcome these limitations, proposed methods rely on training GNNs in smaller number of nodes, and then transferring the GNN to larger graphs. Even though these methods are able to bound the difference between the output of the GNN with different number of nodes, they do not provide guarantees against the optimal GNN on the very large graph. In this paper, we propose to learn GNNs on very large graphs by leveraging the limit object of a sequence of growing graphs, the graphon. We propose to grow the size of the graph as we train, and we show that our proposed methodology -- learning by transference -- converges to a neighborhood of a first order stationary point on the graphon data. A numerical experiment validates our proposed approach.
Learning Globally Smooth Functions on Manifolds
Oct 01, 2022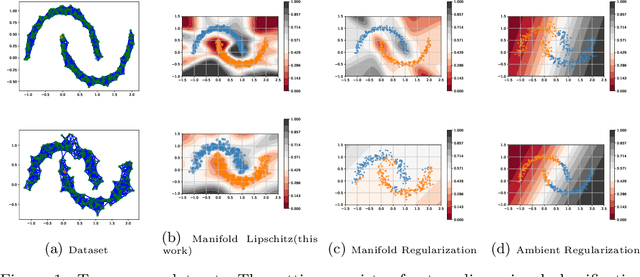

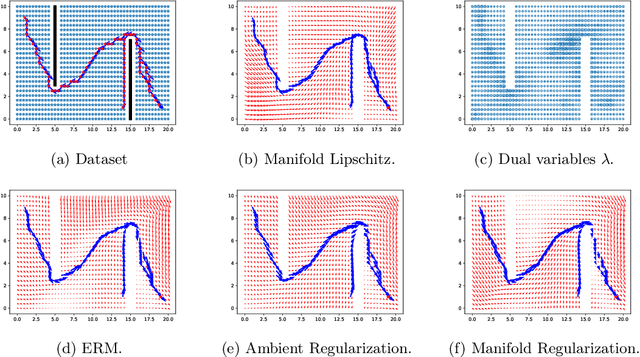

Abstract:Smoothness and low dimensional structures play central roles in improving generalization and stability in learning and statistics. The combination of these properties has led to many advances in semi-supervised learning, generative modeling, and control of dynamical systems. However, learning smooth functions is generally challenging, except in simple cases such as learning linear or kernel models. Typical methods are either too conservative, relying on crude upper bounds such as spectral normalization, too lax, penalizing smoothness on average, or too computationally intensive, requiring the solution of large-scale semi-definite programs. These issues are only exacerbated when trying to simultaneously exploit low dimensionality using, e.g., manifolds. This work proposes to overcome these obstacles by combining techniques from semi-infinite constrained learning and manifold regularization. To do so, it shows that, under typical conditions, the problem of learning a Lipschitz continuous function on a manifold is equivalent to a dynamically weighted manifold regularization problem. This observation leads to a practical algorithm based on a weighted Laplacian penalty whose weights are adapted using stochastic gradient techniques. We prove that, under mild conditions, this method estimates the Lipschitz constant of the solution, learning a globally smooth solution as a byproduct. Numerical examples illustrate the advantages of using this method to impose global smoothness on manifolds as opposed to imposing smoothness on average.
Federated Representation Learning via Maximal Coding Rate Reduction
Oct 01, 2022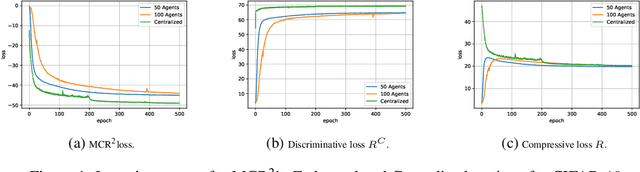
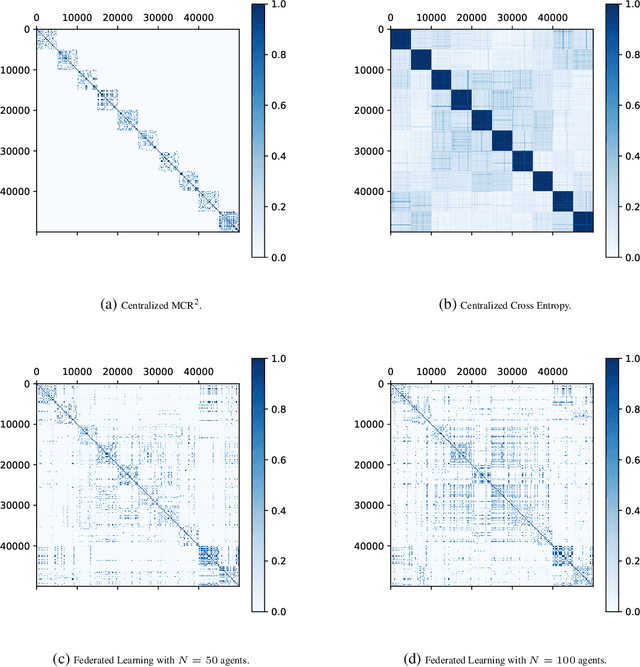
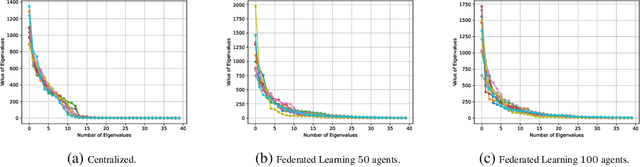
Abstract:We propose a federated methodology to learn low-dimensional representations from a dataset that is distributed among several clients. In particular, we move away from the commonly-used cross-entropy loss in federated learning, and seek to learn shared low-dimensional representations of the data in a decentralized manner via the principle of maximal coding rate reduction (MCR2). Our proposed method, which we refer to as FLOW, utilizes MCR2 as the objective of choice, hence resulting in representations that are both between-class discriminative and within-class compressible. We theoretically show that our distributed algorithm achieves a first-order stationary point. Moreover, we demonstrate, via numerical experiments, the utility of the learned low-dimensional representations.
Training Stable Graph Neural Networks Through Constrained Learning
Oct 07, 2021
Abstract:Graph Neural Networks (GNN) rely on graph convolutions to learn features from network data. GNNs are stable to different types of perturbations of the underlying graph, a property that they inherit from graph filters. In this paper we leverage the stability property of GNNs as a typing point in order to seek for representations that are stable within a distribution. We propose a novel constrained learning approach by imposing a constraint on the stability condition of the GNN within a perturbation of choice. We showcase our framework in real world data, corroborating that we are able to obtain more stable representations while not compromising the overall accuracy of the predictor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge