Luana Ruiz
Dirichlet Meets Horvitz and Thompson: Estimating Homophily in Large Networks via Sampling
Dec 18, 2025


Abstract:Assessing homophily in large-scale networks is central to understanding structural regularities in graphs, and thus inform the choice of models (such as graph neural networks) adopted to learn from network data. Evaluation of smoothness metrics requires access to the entire network topology and node features, which may be impractical in several large-scale, dynamic, resource-limited, or privacy-constrained settings. In this work, we propose a sampling-based framework to estimate homophily via the Dirichlet energy (Laplacian-based total variation) of graph signals, leveraging the Horvitz-Thompson (HT) estimator for unbiased inference from partial graph observations. The Dirichlet energy is a so-termed total (of squared nodal feature deviations) over graph edges; hence, estimable under general network sampling designs for which edge-inclusion probabilities can be analytically derived and used as weights in the proposed HT estimator. We establish that the Dirichlet energy can be consistently estimated from sampled graphs, and empirically study other heterophily measures as well. Experiments on several heterophilic benchmark datasets demonstrate the effectiveness of the proposed HT estimators in reliably capturing homophilic structure (or lack thereof) from sampled network measurements.
Graph Semi-Supervised Learning for Point Classification on Data Manifolds
Jun 13, 2025Abstract:We propose a graph semi-supervised learning framework for classification tasks on data manifolds. Motivated by the manifold hypothesis, we model data as points sampled from a low-dimensional manifold $\mathcal{M} \subset \mathbb{R}^F$. The manifold is approximated in an unsupervised manner using a variational autoencoder (VAE), where the trained encoder maps data to embeddings that represent their coordinates in $\mathbb{R}^F$. A geometric graph is constructed with Gaussian-weighted edges inversely proportional to distances in the embedding space, transforming the point classification problem into a semi-supervised node classification task on the graph. This task is solved using a graph neural network (GNN). Our main contribution is a theoretical analysis of the statistical generalization properties of this data-to-manifold-to-graph pipeline. We show that, under uniform sampling from $\mathcal{M}$, the generalization gap of the semi-supervised task diminishes with increasing graph size, up to the GNN training error. Leveraging a training procedure which resamples a slightly larger graph at regular intervals during training, we then show that the generalization gap can be reduced even further, vanishing asymptotically. Finally, we validate our findings with numerical experiments on image classification benchmarks, demonstrating the empirical effectiveness of our approach.
Local Distance-Preserving Node Embeddings and Their Performance on Random Graphs
Apr 11, 2025Abstract:Learning node representations is a fundamental problem in graph machine learning. While existing embedding methods effectively preserve local similarity measures, they often fail to capture global functions like graph distances. Inspired by Bourgain's seminal work on Hilbert space embeddings of metric spaces (1985), we study the performance of local distance-preserving node embeddings. Known as landmark-based algorithms, these embeddings approximate pairwise distances by computing shortest paths from a small subset of reference nodes (i.e., landmarks). Our main theoretical contribution shows that random graphs, such as Erd\H{o}s-R\'enyi random graphs, require lower dimensions in landmark-based embeddings compared to worst-case graphs. Empirically, we demonstrate that the GNN-based approximations for the distances to landmarks generalize well to larger networks, offering a scalable alternative for graph representation learning.
Subsampling Graphs with GNN Performance Guarantees
Feb 23, 2025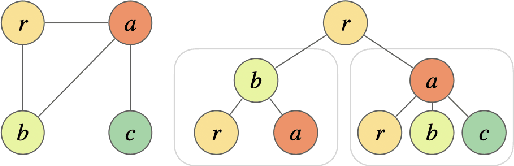
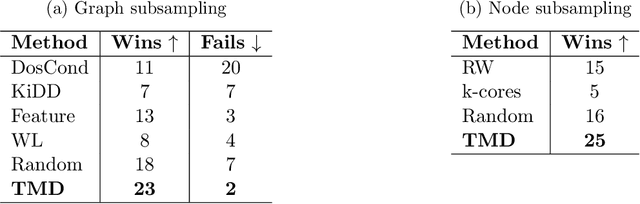
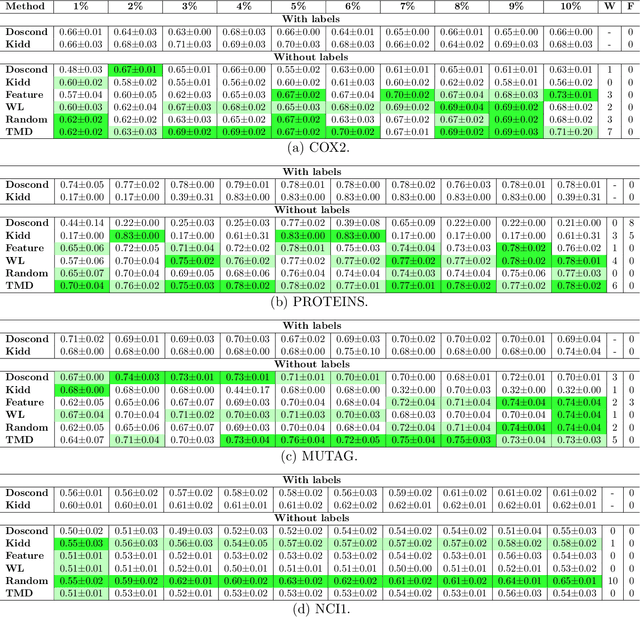
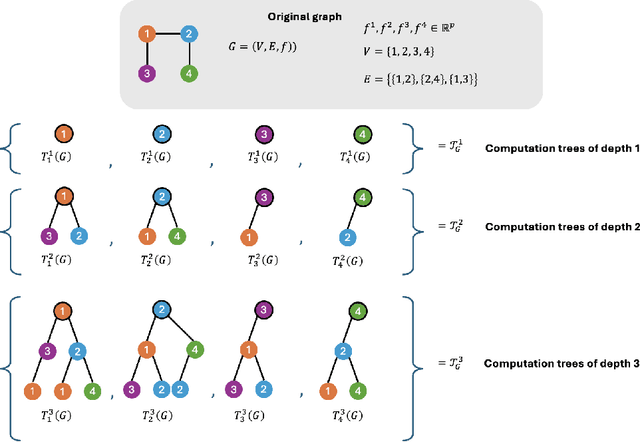
Abstract:How can we subsample graph data so that a graph neural network (GNN) trained on the subsample achieves performance comparable to training on the full dataset? This question is of fundamental interest, as smaller datasets reduce labeling costs, storage requirements, and computational resources needed for training. Selecting an effective subset is challenging: a poorly chosen subsample can severely degrade model performance, and empirically testing multiple subsets for quality obviates the benefits of subsampling. Therefore, it is critical that subsampling comes with guarantees on model performance. In this work, we introduce new subsampling methods for graph datasets that leverage the Tree Mover's Distance to reduce both the number of graphs and the size of individual graphs. To our knowledge, our approach is the first that is supported by rigorous theoretical guarantees: we prove that training a GNN on the subsampled data results in a bounded increase in loss compared to training on the full dataset. Unlike existing methods, our approach is both model-agnostic, requiring minimal assumptions about the GNN architecture, and label-agnostic, eliminating the need to label the full training set. This enables subsampling early in the model development pipeline (before data annotation, model selection, and hyperparameter tuning) reducing costs and resources needed for storage, labeling, and training. We validate our theoretical results with experiments showing that our approach outperforms existing subsampling methods across multiple datasets.
Graph Sampling for Scalable and Expressive Graph Neural Networks on Homophilic Graphs
Oct 22, 2024Abstract:Graph Neural Networks (GNNs) excel in many graph machine learning tasks but face challenges when scaling to large networks. GNN transferability allows training on smaller graphs and applying the model to larger ones, but existing methods often rely on random subsampling, leading to disconnected subgraphs and reduced model expressivity. We propose a novel graph sampling algorithm that leverages feature homophily to preserve graph structure. By minimizing the trace of the data correlation matrix, our method better preserves the graph Laplacian's rank than random sampling while achieving lower complexity than spectral methods. Experiments on citation networks show improved performance in preserving graph rank and GNN transferability compared to random sampling.
Reply to 'Comments on Graphon Signal Processing' [arXiv:2310.14683]
Jan 05, 2024Abstract:This technical note addresses an issue [arXiv:2310.14683] with the proof (but not the statement) of [arXiv:2003.05030, Proposition 4]. The statement of the proposition is correct, but the proof as written in [arXiv:2003.05030] is not and due to a typo in the manuscript, a reference to the correct proof is effectively missing. In the sequel, we present [arXiv:2003.05030, Proposition 4] and its proof. The proof follows from results in [2] that we reproduce here for clarity of exposition. Since the statement of the proposition remains correct, no change in the results of [arXiv:2003.05030] are required. In particular, Lemma 3 and Lemma 4 showing spectral convergence of graphs to graphons, Theorem 1 showing convergence of the GFT to the WFT, and Theorems 3 and 4 showing convergence of graph to graphon filters, remain valid.
A Poincaré Inequality and Consistency Results for Signal Sampling on Large Graphs
Nov 17, 2023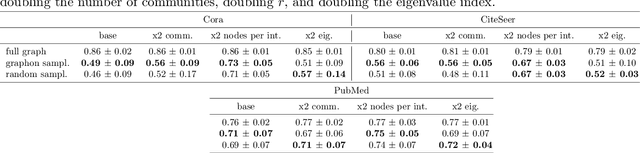


Abstract:Large-scale graph machine learning is challenging as the complexity of learning models scales with the graph size. Subsampling the graph is a viable alternative, but sampling on graphs is nontrivial as graphs are non-Euclidean. Existing graph sampling techniques require not only computing the spectra of large matrices but also repeating these computations when the graph changes, e.g., grows. In this paper, we introduce a signal sampling theory for a type of graph limit -- the graphon. We prove a Poincar\'e inequality for graphon signals and show that complements of node subsets satisfying this inequality are unique sampling sets for Paley-Wiener spaces of graphon signals. Exploiting connections with spectral clustering and Gaussian elimination, we prove that such sampling sets are consistent in the sense that unique sampling sets on a convergent graph sequence converge to unique sampling sets on the graphon. We then propose a related graphon signal sampling algorithm for large graphs, and demonstrate its good empirical performance on graph machine learning tasks.
A Local Graph Limits Perspective on Sampling-Based GNNs
Oct 17, 2023



Abstract:We propose a theoretical framework for training Graph Neural Networks (GNNs) on large input graphs via training on small, fixed-size sampled subgraphs. This framework is applicable to a wide range of models, including popular sampling-based GNNs, such as GraphSAGE and FastGCN. Leveraging the theory of graph local limits, we prove that, under mild assumptions, parameters learned from training sampling-based GNNs on small samples of a large input graph are within an $\epsilon$-neighborhood of the outcome of training the same architecture on the whole graph. We derive bounds on the number of samples, the size of the graph, and the training steps required as a function of $\epsilon$. Our results give a novel theoretical understanding for using sampling in training GNNs. They also suggest that by training GNNs on small samples of the input graph, practitioners can identify and select the best models, hyperparameters, and sampling algorithms more efficiently. We empirically illustrate our results on a node classification task on large citation graphs, observing that sampling-based GNNs trained on local subgraphs 12$\times$ smaller than the original graph achieve comparable performance to those trained on the input graph.
Geometric Graph Filters and Neural Networks: Limit Properties and Discriminability Trade-offs
May 29, 2023Abstract:This paper studies the relationship between a graph neural network (GNN) and a manifold neural network (MNN) when the graph is constructed from a set of points sampled from the manifold, thus encoding geometric information. We consider convolutional MNNs and GNNs where the manifold and the graph convolutions are respectively defined in terms of the Laplace-Beltrami operator and the graph Laplacian. Using the appropriate kernels, we analyze both dense and moderately sparse graphs. We prove non-asymptotic error bounds showing that convolutional filters and neural networks on these graphs converge to convolutional filters and neural networks on the continuous manifold. As a byproduct of this analysis, we observe an important trade-off between the discriminability of graph filters and their ability to approximate the desired behavior of manifold filters. We then discuss how this trade-off is ameliorated in neural networks due to the frequency mixing property of nonlinearities. We further derive a transferability corollary for geometric graphs sampled from the same manifold. We validate our results numerically on a navigation control problem and a point cloud classification task.
Graph Neural Tangent Kernel: Convergence on Large Graphs
Jan 25, 2023
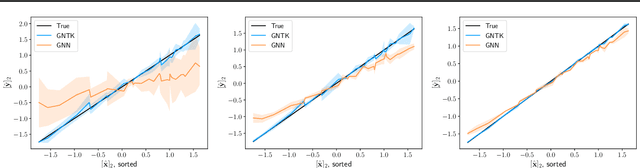
Abstract:Graph neural networks (GNNs) achieve remarkable performance in graph machine learning tasks but can be hard to train on large-graph data, where their learning dynamics are not well understood. We investigate the training dynamics of large-graph GNNs using graph neural tangent kernels (GNTKs) and graphons. In the limit of large width, optimization of an overparametrized NN is equivalent to kernel regression on the NTK. Here, we investigate how the GNTK evolves as another independent dimension is varied: the graph size. We use graphons to define limit objects -- graphon NNs for GNNs, and graphon NTKs for GNTKs, and prove that, on a sequence of growing graphs, the GNTKs converge to the graphon NTK. We further prove that the eigenspaces of the GNTK, which are related to the problem learning directions and associated learning speeds, converge to the spectrum of the GNTK. This implies that in the large-graph limit, the GNTK fitted on a graph of moderate size can be used to solve the same task on the large-graph and infer the learning dynamics of the large-graph GNN. These results are verified empirically on node regression and node classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge