Ellen Vitercik
Bridged Clustering for Representation Learning: Semi-Supervised Sparse Bridging
Oct 08, 2025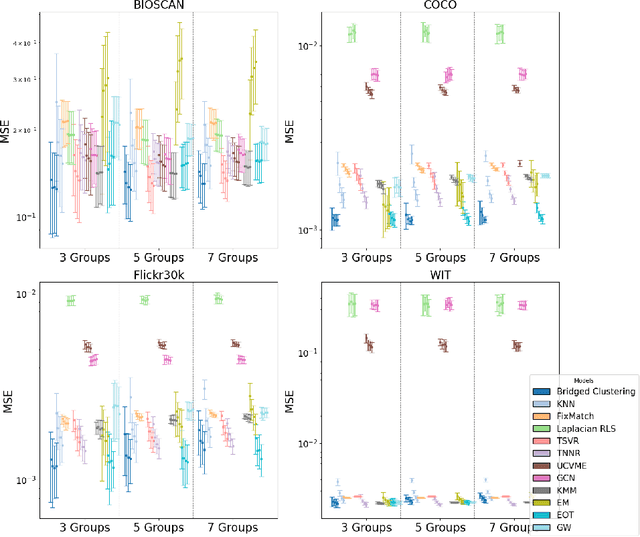
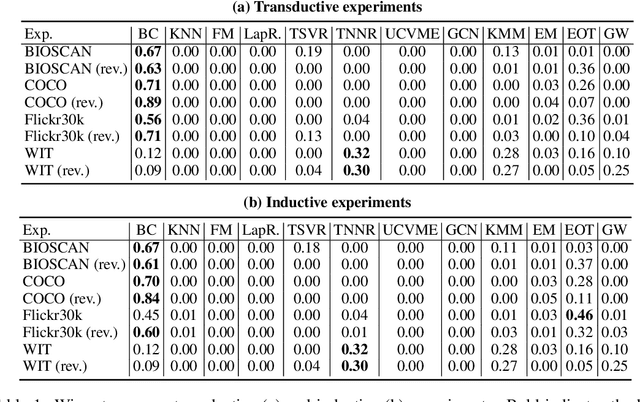

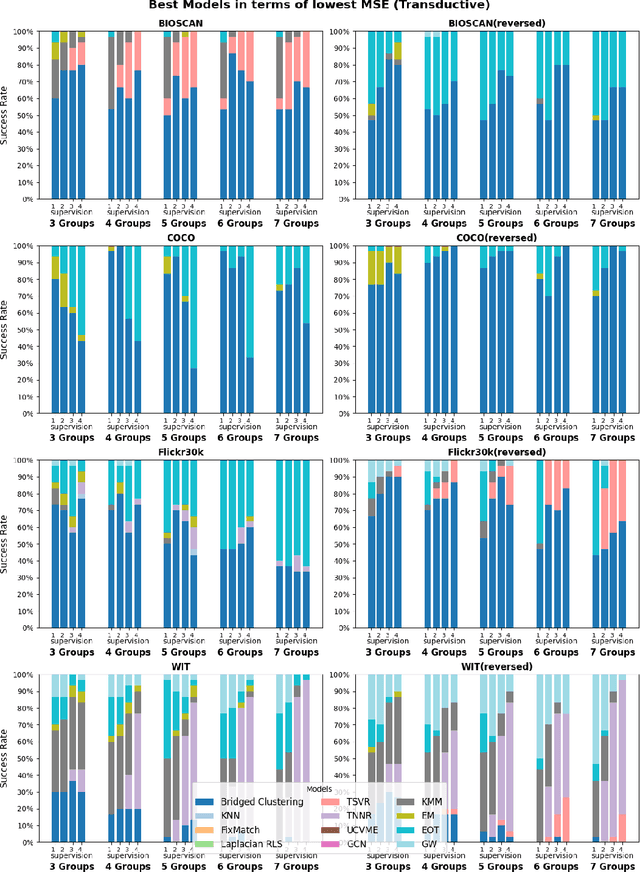
Abstract:We introduce Bridged Clustering, a semi-supervised framework to learn predictors from any unpaired input $X$ and output $Y$ dataset. Our method first clusters $X$ and $Y$ independently, then learns a sparse, interpretable bridge between clusters using only a few paired examples. At inference, a new input $x$ is assigned to its nearest input cluster, and the centroid of the linked output cluster is returned as the prediction $\hat{y}$. Unlike traditional SSL, Bridged Clustering explicitly leverages output-only data, and unlike dense transport-based methods, it maintains a sparse and interpretable alignment. Through theoretical analysis, we show that with bounded mis-clustering and mis-bridging rates, our algorithm becomes an effective and efficient predictor. Empirically, our method is competitive with SOTA methods while remaining simple, model-agnostic, and highly label-efficient in low-supervision settings.
Primal-Dual Neural Algorithmic Reasoning
May 29, 2025Abstract:Neural Algorithmic Reasoning (NAR) trains neural networks to simulate classical algorithms, enabling structured and interpretable reasoning over complex data. While prior research has predominantly focused on learning exact algorithms for polynomial-time-solvable problems, extending NAR to harder problems remains an open challenge. In this work, we introduce a general NAR framework grounded in the primal-dual paradigm, a classical method for designing efficient approximation algorithms. By leveraging a bipartite representation between primal and dual variables, we establish an alignment between primal-dual algorithms and Graph Neural Networks. Furthermore, we incorporate optimal solutions from small instances to greatly enhance the model's reasoning capabilities. Our empirical results demonstrate that our model not only simulates but also outperforms approximation algorithms for multiple tasks, exhibiting robust generalization to larger and out-of-distribution graphs. Moreover, we highlight the framework's practical utility by integrating it with commercial solvers and applying it to real-world datasets.
DSR-Bench: Evaluating the Structural Reasoning Abilities of LLMs via Data Structures
May 29, 2025Abstract:Large language models (LLMs) are increasingly deployed for real-world tasks that fundamentally involve data manipulation. A core requirement across these tasks is the ability to perform structural reasoning--that is, to understand and reason about data relationships. For example, customer requests require a temporal ordering, which can be represented by data structures such as queues. However, existing benchmarks primarily focus on high-level, application-driven evaluations without isolating this fundamental capability. To address this gap, we introduce DSR-Bench, a novel benchmark evaluating LLMs' structural reasoning capabilities through data structures, which provide interpretable representations of data relationships. DSR-Bench includes 20 data structures, 35 operations, and 4,140 problem instances, organized hierarchically for fine-grained analysis of reasoning limitations. Our evaluation pipeline is fully automated and deterministic, eliminating subjective human or model-based judgments. Its synthetic nature also ensures scalability and minimizes data contamination risks. We benchmark nine state-of-the-art LLMs. Our analysis shows that instruction-tuned models struggle with basic multi-attribute and multi-hop reasoning. Furthermore, while reasoning-oriented models perform better, they remain fragile on complex and hybrid structures, with the best model achieving an average score of only 47% on the challenge subset. Crucially, models often perform poorly on multi-dimensional data and natural language task descriptions, highlighting a critical gap for real-world deployment.
Subsampling Graphs with GNN Performance Guarantees
Feb 23, 2025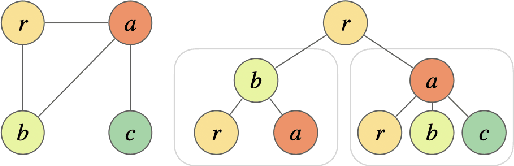
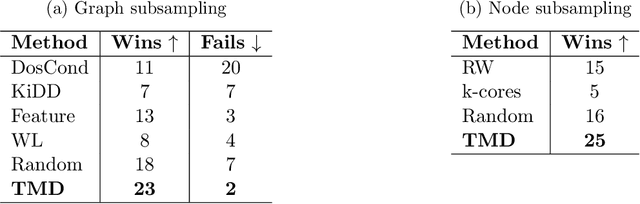
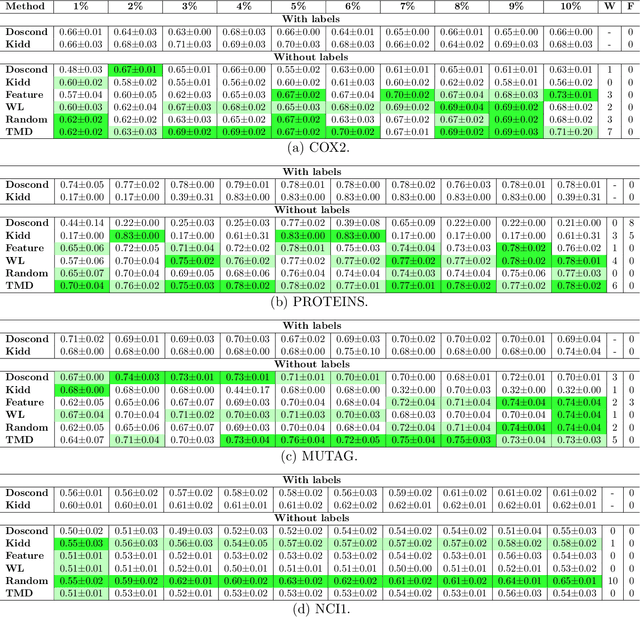
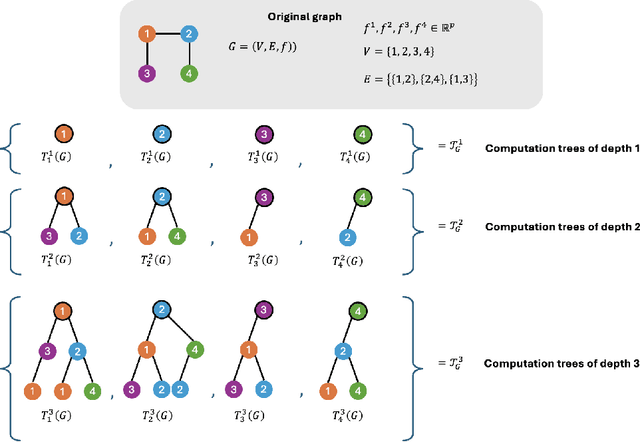
Abstract:How can we subsample graph data so that a graph neural network (GNN) trained on the subsample achieves performance comparable to training on the full dataset? This question is of fundamental interest, as smaller datasets reduce labeling costs, storage requirements, and computational resources needed for training. Selecting an effective subset is challenging: a poorly chosen subsample can severely degrade model performance, and empirically testing multiple subsets for quality obviates the benefits of subsampling. Therefore, it is critical that subsampling comes with guarantees on model performance. In this work, we introduce new subsampling methods for graph datasets that leverage the Tree Mover's Distance to reduce both the number of graphs and the size of individual graphs. To our knowledge, our approach is the first that is supported by rigorous theoretical guarantees: we prove that training a GNN on the subsampled data results in a bounded increase in loss compared to training on the full dataset. Unlike existing methods, our approach is both model-agnostic, requiring minimal assumptions about the GNN architecture, and label-agnostic, eliminating the need to label the full training set. This enables subsampling early in the model development pipeline (before data annotation, model selection, and hyperparameter tuning) reducing costs and resources needed for storage, labeling, and training. We validate our theoretical results with experiments showing that our approach outperforms existing subsampling methods across multiple datasets.
EquivaMap: Leveraging LLMs for Automatic Equivalence Checking of Optimization Formulations
Feb 20, 2025



Abstract:A fundamental problem in combinatorial optimization is identifying equivalent formulations, which can lead to more efficient solution strategies and deeper insights into a problem's computational complexity. The need to automatically identify equivalence between problem formulations has grown as optimization copilots--systems that generate problem formulations from natural language descriptions--have proliferated. However, existing approaches to checking formulation equivalence lack grounding, relying on simple heuristics which are insufficient for rigorous validation. Inspired by Karp reductions, in this work we introduce quasi-Karp equivalence, a formal criterion for determining when two optimization formulations are equivalent based on the existence of a mapping between their decision variables. We propose EquivaMap, a framework that leverages large language models to automatically discover such mappings, enabling scalable and reliable equivalence verification. To evaluate our approach, we construct the first open-source dataset of equivalent optimization formulations, generated by applying transformations such as adding slack variables or valid inequalities to existing formulations. Empirically, EquivaMap significantly outperforms existing methods, achieving substantial improvements in correctly identifying formulation equivalence.
Algorithms with Calibrated Machine Learning Predictions
Feb 05, 2025Abstract:The field of algorithms with predictions incorporates machine learning advice in the design of online algorithms to improve real-world performance. While this theoretical framework often assumes uniform reliability across all predictions, modern machine learning models can now provide instance-level uncertainty estimates. In this paper, we propose calibration as a principled and practical tool to bridge this gap, demonstrating the benefits of calibrated advice through two case studies: the ski rental and online job scheduling problems. For ski rental, we design an algorithm that achieves optimal prediction-dependent performance and prove that, in high-variance settings, calibrated advice offers more effective guidance than alternative methods for uncertainty quantification. For job scheduling, we demonstrate that using a calibrated predictor leads to significant performance improvements over existing methods. Evaluations on real-world data validate our theoretical findings, highlighting the practical impact of calibration for algorithms with predictions.
LLMs for Cold-Start Cutting Plane Separator Configuration
Dec 16, 2024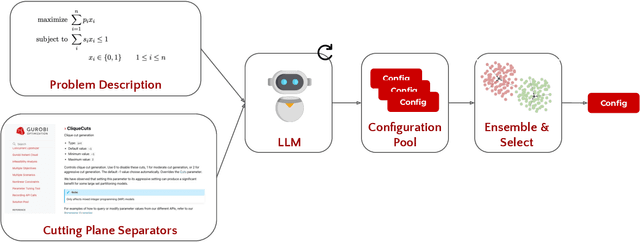
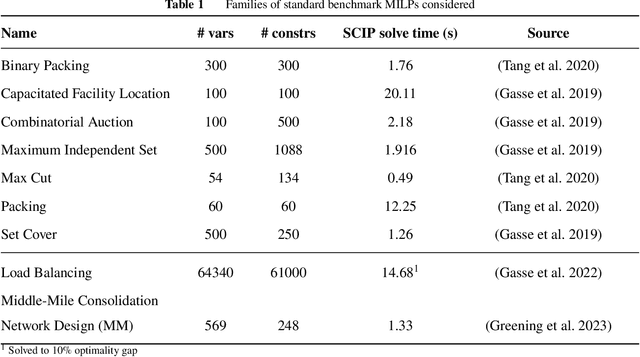

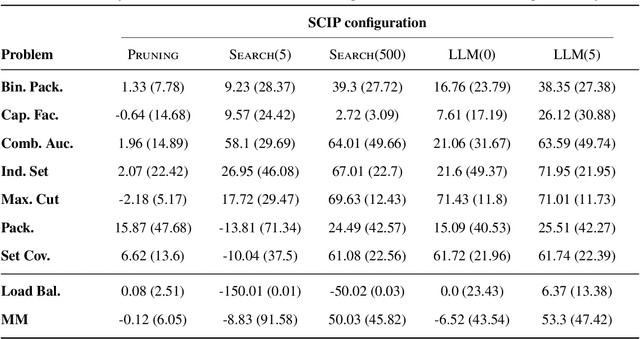
Abstract:Mixed integer linear programming (MILP) solvers ship with a staggering number of parameters that are challenging to select a priori for all but expert optimization users, but can have an outsized impact on the performance of the MILP solver. Existing machine learning (ML) approaches to configure solvers require training ML models by solving thousands of related MILP instances, generalize poorly to new problem sizes, and often require implementing complex ML pipelines and custom solver interfaces that can be difficult to integrate into existing optimization workflows. In this paper, we introduce a new LLM-based framework to configure which cutting plane separators to use for a given MILP problem with little to no training data based on characteristics of the instance, such as a natural language description of the problem and the associated LaTeX formulation. We augment these LLMs with descriptions of cutting plane separators available in a given solver, grounded by summarizing the existing research literature on separators. While individual solver configurations have a large variance in performance, we present a novel ensembling strategy that clusters and aggregates configurations to create a small portfolio of high-performing configurations. Our LLM-based methodology requires no custom solver interface, can find a high-performing configuration by solving only a small number of MILPs, and can generate the configuration with simple API calls that run in under a second. Numerical results show our approach is competitive with existing configuration approaches on a suite of classic combinatorial optimization problems and real-world datasets with only a fraction of the training data and computation time.
Wait-Less Offline Tuning and Re-solving for Online Decision Making
Dec 12, 2024Abstract:Online linear programming (OLP) has found broad applications in revenue management and resource allocation. State-of-the-art OLP algorithms achieve low regret by repeatedly solving linear programming (LP) subproblems that incorporate updated resource information. However, LP-based methods are computationally expensive and often inefficient for large-scale applications. In contrast, recent first-order OLP algorithms are more computationally efficient but typically suffer from worse regret guarantees. To address these shortcomings, we propose a new algorithm that combines the strengths of LP-based and first-order OLP methods. The algorithm re-solves the LP subproblems periodically at a predefined frequency $f$ and uses the latest dual prices to guide online decision-making. In addition, a first-order method runs in parallel during each interval between LP re-solves, smoothing resource consumption. Our algorithm achieves $\mathscr{O}(\log (T/f) + \sqrt{f})$ regret, delivering a "wait-less" online decision-making process that balances the computational efficiency of first-order methods and the superior regret guarantee of LP-based methods.
Algorithmic Content Selection and the Impact of User Disengagement
Oct 17, 2024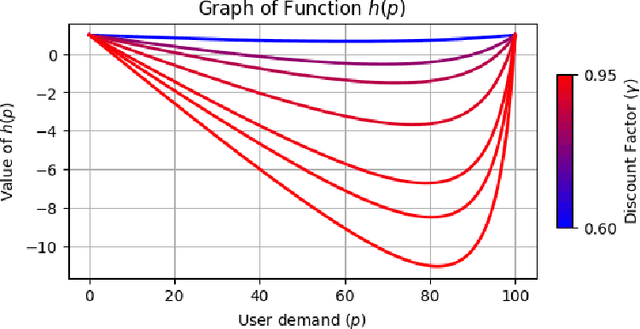
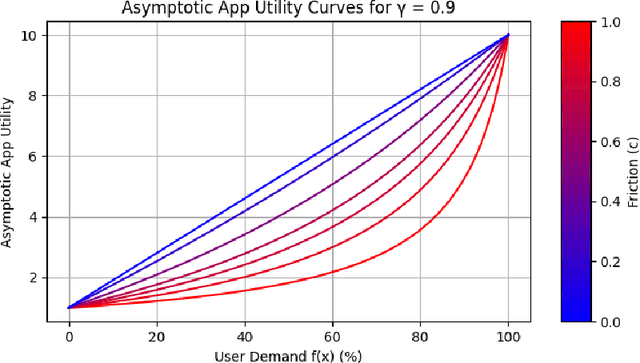
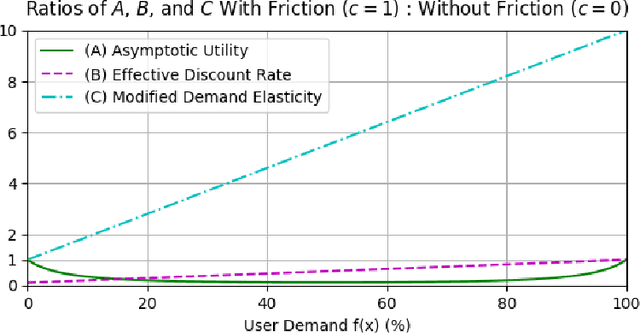
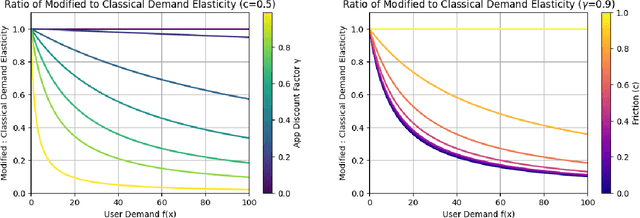
Abstract:The content selection problem of digital services is often modeled as a decision-process where a service chooses, over multiple rounds, an arm to pull from a set of arms that each return a certain reward. This classical model does not account for the possibility that users disengage when dissatisfied and thus fails to capture an important trade-off between choosing content that promotes future engagement versus immediate reward. In this work, we introduce a model for the content selection problem where dissatisfied users may disengage and where the content that maximizes immediate reward does not necessarily maximize the odds of future user engagement. We show that when the relationship between each arm's expected reward and effect on user satisfaction are linearly related, an optimal content selection policy can be computed efficiently with dynamic programming under natural assumptions about the complexity of the users' engagement patterns. Moreover, we show that in an online learning setting where users with unknown engagement patterns arrive, there is a variant of Hedge that attains a $\tfrac 12$-competitive ratio regret bound. We also use our model to identify key primitives that determine how digital services should weigh engagement against revenue. For example, when it is more difficult for users to rejoin a service they are disengaged from, digital services naturally see a reduced payoff but user engagement may -- counterintuitively -- increase.
MAGNOLIA: Matching Algorithms via GNNs for Online Value-to-go Approximation
Jun 10, 2024Abstract:Online Bayesian bipartite matching is a central problem in digital marketplaces and exchanges, including advertising, crowdsourcing, ridesharing, and kidney exchange. We introduce a graph neural network (GNN) approach that emulates the problem's combinatorially-complex optimal online algorithm, which selects actions (e.g., which nodes to match) by computing each action's value-to-go (VTG) -- the expected weight of the final matching if the algorithm takes that action, then acts optimally in the future. We train a GNN to estimate VTG and show empirically that this GNN returns high-weight matchings across a variety of tasks. Moreover, we identify a common family of graph distributions in spatial crowdsourcing applications, such as rideshare, under which VTG can be efficiently approximated by aggregating information within local neighborhoods in the graphs. This structure matches the local behavior of GNNs, providing theoretical justification for our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge