Small Gradient Norm Regret for Online Convex Optimization

This paper introduces a new problem-dependent regret measure for online convex optimization with smooth losses. The notion, which we call the $G^\star$ regret, depends on the cumulative squared gradient norm evaluated at the decision in hindsight $\sum_{t=1}^T \|\nabla \ell(x^\star)\|^2$. We show that the $G^\star$ regret strictly refines the existing $L^\star$ (small loss) regret, and that it can be arbitrarily sharper when the losses have vanishing curvature around the hindsight decision. We establish upper and lower bounds on the $G^\star$ regret and extend our results to dynamic regret and bandit settings. As a byproduct, we refine the existing convergence analysis of stochastic optimization algorithms in the interpolation regime. Some experiments validate our theoretical findings.

Gradient Methods with Online Scaling Part I. Theoretical Foundations

This paper establishes the theoretical foundations of the online scaled gradient methods (OSGM), a framework that utilizes online learning to adapt stepsizes and provably accelerate first-order methods. OSGM quantifies the effectiveness of a stepsize by a feedback function motivated from a convergence measure and uses the feedback to adjust the stepsize through an online learning algorithm. Consequently, instantiations of OSGM achieve convergence rates that are asymptotically no worse than the optimal stepsize. OSGM yields desirable convergence guarantees on smooth convex problems, including 1) trajectory-dependent global convergence on smooth convex objectives; 2) an improved complexity result on smooth strongly convex problems, and 3) local superlinear convergence. Notably, OSGM constitutes a new family of first-order methods with non-asymptotic superlinear convergence, joining the celebrated quasi-Newton methods. Finally, OSGM explains the empirical success of the popular hypergradient-descent heuristic in optimization for machine learning.

Beyond $\mathcal{O}(\sqrt{T})$ Regret: Decoupling Learning and Decision-making in Online Linear Programming

Online linear programming plays an important role in both revenue management and resource allocation, and recent research has focused on developing efficient first-order online learning algorithms. Despite the empirical success of first-order methods, they typically achieve a regret no better than $\mathcal{O} ( \sqrt{T} )$, which is suboptimal compared to the $\mathcal{O} (\log T)$ bound guaranteed by the state-of-the-art linear programming (LP)-based online algorithms. This paper establishes a general framework that improves upon the $\mathcal{O} ( \sqrt{T} )$ result when the LP dual problem exhibits certain error bound conditions. For the first time, we show that first-order learning algorithms achieve $o( \sqrt{T} )$ regret in the continuous support setting and $\mathcal{O} (\log T)$ regret in the finite support setting beyond the non-degeneracy assumption. Our results significantly improve the state-of-the-art regret results and provide new insights for sequential decision-making.

Wait-Less Offline Tuning and Re-solving for Online Decision Making

Online linear programming (OLP) has found broad applications in revenue management and resource allocation. State-of-the-art OLP algorithms achieve low regret by repeatedly solving linear programming (LP) subproblems that incorporate updated resource information. However, LP-based methods are computationally expensive and often inefficient for large-scale applications. In contrast, recent first-order OLP algorithms are more computationally efficient but typically suffer from worse regret guarantees. To address these shortcomings, we propose a new algorithm that combines the strengths of LP-based and first-order OLP methods. The algorithm re-solves the LP subproblems periodically at a predefined frequency $f$ and uses the latest dual prices to guide online decision-making. In addition, a first-order method runs in parallel during each interval between LP re-solves, smoothing resource consumption. Our algorithm achieves $\mathscr{O}(\log (T/f) + \sqrt{f})$ regret, delivering a "wait-less" online decision-making process that balances the computational efficiency of first-order methods and the superior regret guarantee of LP-based methods.

Gradient Methods with Online Scaling

We introduce a framework to accelerate the convergence of gradient-based methods with online learning. The framework learns to scale the gradient at each iteration through an online learning algorithm and provably accelerates gradient-based methods asymptotically. In contrast with previous literature, where convergence is established based on worst-case analysis, our framework provides a strong convergence guarantee with respect to the optimal scaling matrix for the iteration trajectory. For smooth strongly convex optimization, our results provide an $O(\kappa^\star \log(1/\varepsilon)$) complexity result, where $\kappa^\star$ is the condition number achievable by the optimal preconditioner, improving on the previous $O(\sqrt{n}\kappa^\star \log(1/\varepsilon))$ result. In particular, a variant of our method achieves superlinear convergence on convex quadratics. For smooth convex optimization, we show for the first time that the widely-used hypergradient descent heuristic improves on the convergence of gradient descent.

OptiMUS-0.3: Using Large Language Models to Model and Solve Optimization Problems at Scale

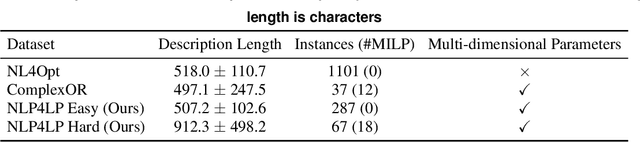
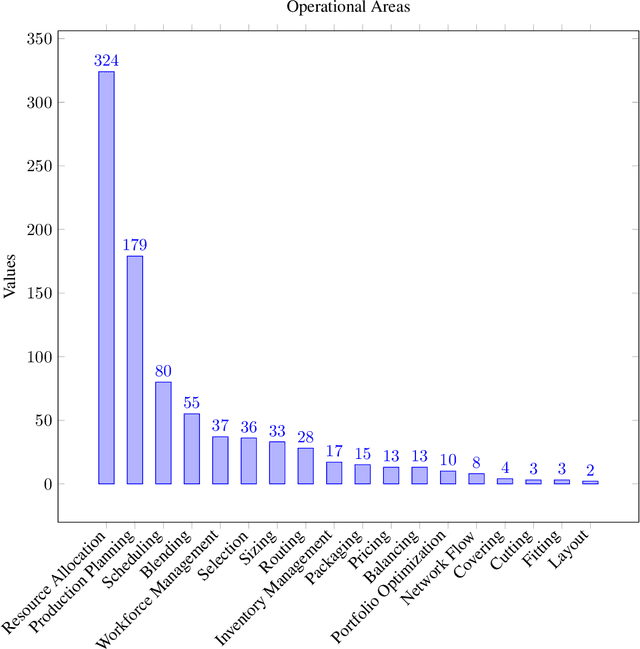
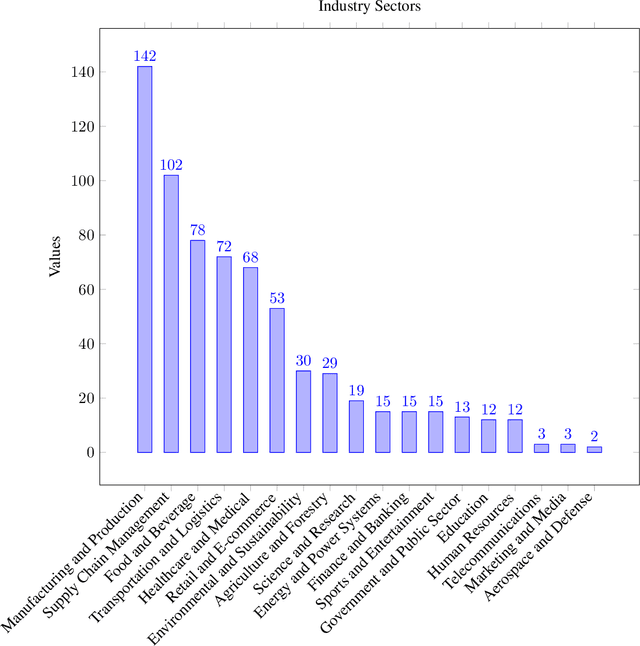
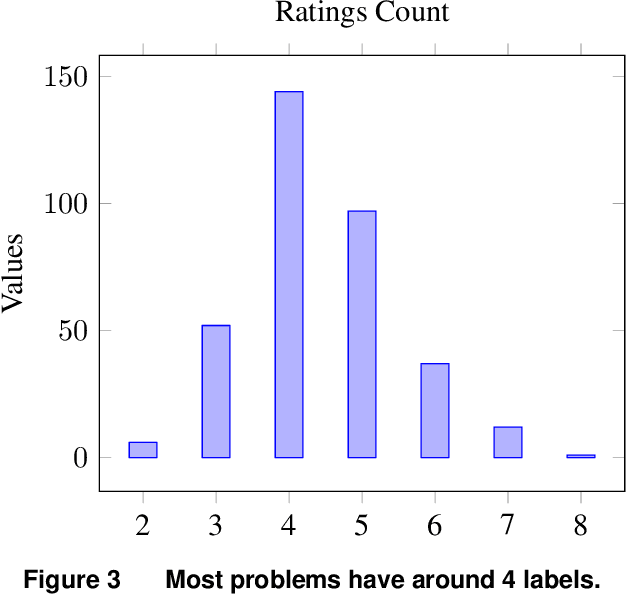
Optimization problems are pervasive in sectors from manufacturing and distribution to healthcare. However, most such problems are still solved heuristically by hand rather than optimally by state-of-the art solvers because the expertise required to formulate and solve these problems limits the widespread adoption of optimization tools and techniques. We introduce a Large Language Model (LLM)-based system designed to formulate and solve (mixed integer) linear programming problems from their natural language descriptions. Our system is capable of developing mathematical models, writing and debugging solver code, evaluating the generated solutions, and improving efficiency and correctness of its model and code based on these evaluations. OptiMUS-0.3 utilizes a modular structure to process problems, allowing it to handle problems with long descriptions and complex data without long prompts. Experiments demonstrate that OptiMUS-0.3 outperforms existing state-of-the-art methods on easy datasets by more than 12% and on hard datasets (including a new dataset, NLP4LP, released with this paper that features long and complex problems) by more than 8%.

OptiMUS: Scalable Optimization Modeling with (MI)LP Solvers and Large Language Models

Optimization problems are pervasive in sectors from manufacturing and distribution to healthcare. However, most such problems are still solved heuristically by hand rather than optimally by state-of-the-art solvers because the expertise required to formulate and solve these problems limits the widespread adoption of optimization tools and techniques. This paper introduces OptiMUS, a Large Language Model (LLM)-based agent designed to formulate and solve (mixed integer) linear programming problems from their natural language descriptions. OptiMUS can develop mathematical models, write and debug solver code, evaluate the generated solutions, and improve its model and code based on these evaluations. OptiMUS utilizes a modular structure to process problems, allowing it to handle problems with long descriptions and complex data without long prompts. Experiments demonstrate that OptiMUS outperforms existing state-of-the-art methods on easy datasets by more than $20\%$ and on hard datasets (including a new dataset, NLP4LP, released with this paper that features long and complex problems) by more than $30\%$.

Decoupling Learning and Decision-Making: Breaking the $\mathcal{O}(\sqrt{T})$ Barrier in Online Resource Allocation with First-Order Methods

Online linear programming plays an important role in both revenue management and resource allocation, and recent research has focused on developing efficient first-order online learning algorithms. Despite the empirical success of first-order methods, they typically achieve a regret no better than $\mathcal{O}(\sqrt{T})$, which is suboptimal compared to the $\mathcal{O}(\log T)$ bound guaranteed by the state-of-the-art linear programming (LP)-based online algorithms. This paper establishes several important facts about online linear programming, which unveils the challenge for first-order-method-based online algorithms to achieve beyond $\mathcal{O}(\sqrt{T})$ regret. To address the challenge, we introduce a new algorithmic framework that decouples learning from decision-making. More importantly, for the first time, we show that first-order methods can attain regret $\mathcal{O}(T^{1/3})$ with this new framework. Lastly, we conduct numerical experiments to validate our theoretical findings.

Stochastic Weakly Convex Optimization Beyond Lipschitz Continuity

This paper considers stochastic weakly convex optimization without the standard Lipschitz continuity assumption. Based on new adaptive regularization (stepsize) strategies, we show that a wide class of stochastic algorithms, including the stochastic subgradient method, preserve the $\mathcal{O} ( 1 / \sqrt{K})$ convergence rate with constant failure rate. Our analyses rest on rather weak assumptions: the Lipschitz parameter can be either bounded by a general growth function of $\|x\|$ or locally estimated through independent random samples.

OptiMUS: Optimization Modeling Using mip Solvers and large language models

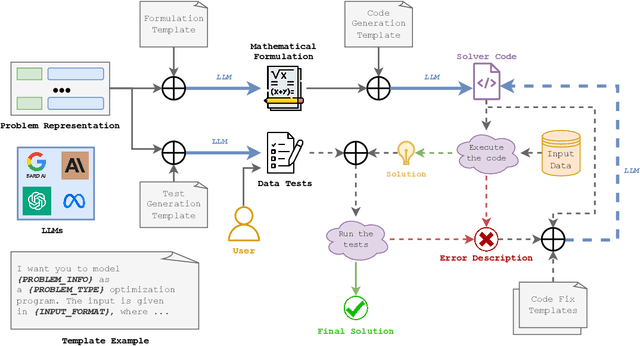
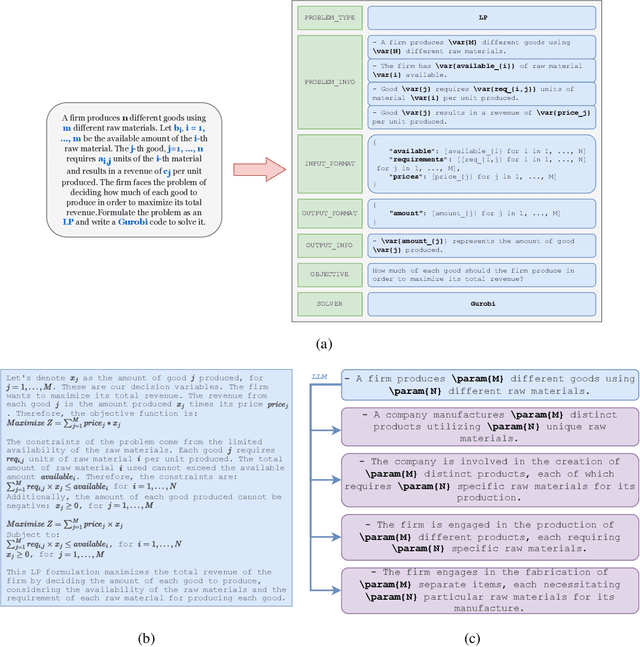
Optimization problems are pervasive across various sectors, from manufacturing and distribution to healthcare. However, most such problems are still solved heuristically by hand rather than optimally by state-of-the-art solvers, as the expertise required to formulate and solve these problems limits the widespread adoption of optimization tools and techniques. We introduce OptiMUS, a Large Language Model (LLM)-based agent designed to formulate and solve MILP problems from their natural language descriptions. OptiMUS is capable of developing mathematical models, writing and debugging solver code, developing tests, and checking the validity of generated solutions. To benchmark our agent, we present NLP4LP, a novel dataset of linear programming (LP) and mixed integer linear programming (MILP) problems. Our experiments demonstrate that OptiMUS is able to solve 67\% more problems compared to a basic LLM prompting strategy. OptiMUS code and NLP4LP dataset are available at \href{https://github.com/teshnizi/OptiMUS}{https://github.com/teshnizi/OptiMUS}