Exploring Audio Cues for Enhanced Test-Time Video Model Adaptation

Test-time adaptation (TTA) aims to boost the generalization capability of a trained model by conducting self-/unsupervised learning during the testing phase. While most existing TTA methods for video primarily utilize visual supervisory signals, they often overlook the potential contribution of inherent audio data. To address this gap, we propose a novel approach that incorporates audio information into video TTA. Our method capitalizes on the rich semantic content of audio to generate audio-assisted pseudo-labels, a new concept in the context of video TTA. Specifically, we propose an audio-to-video label mapping method by first employing pre-trained audio models to classify audio signals extracted from videos and then mapping the audio-based predictions to video label spaces through large language models, thereby establishing a connection between the audio categories and video labels. To effectively leverage the generated pseudo-labels, we present a flexible adaptation cycle that determines the optimal number of adaptation iterations for each sample, based on changes in loss and consistency across different views. This enables a customized adaptation process for each sample. Experimental results on two widely used datasets (UCF101-C and Kinetics-Sounds-C), as well as on two newly constructed audio-video TTA datasets (AVE-C and AVMIT-C) with various corruption types, demonstrate the superiority of our approach. Our method consistently improves adaptation performance across different video classification models and represents a significant step forward in integrating audio information into video TTA. Code: https://github.com/keikeiqi/Audio-Assisted-TTA.

Learning to Generate Gradients for Test-Time Adaptation via Test-Time Training Layers

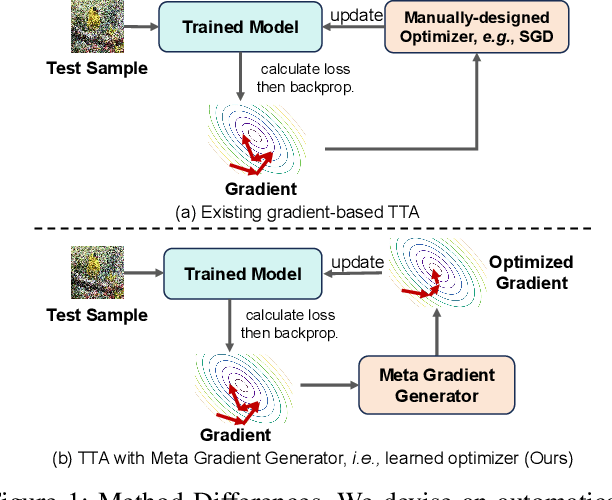
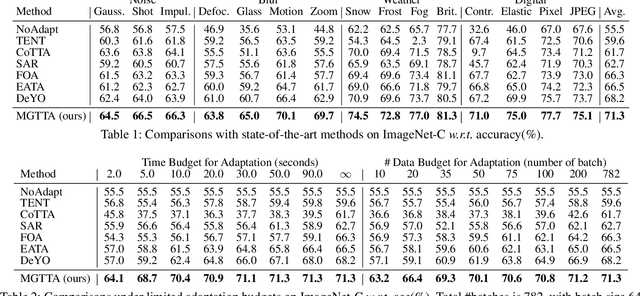
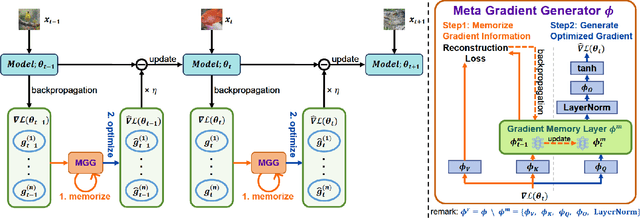
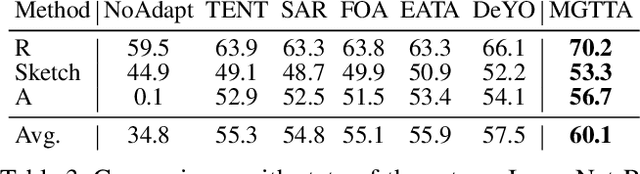
Test-time adaptation (TTA) aims to fine-tune a trained model online using unlabeled testing data to adapt to new environments or out-of-distribution data, demonstrating broad application potential in real-world scenarios. However, in this optimization process, unsupervised learning objectives like entropy minimization frequently encounter noisy learning signals. These signals produce unreliable gradients, which hinder the model ability to converge to an optimal solution quickly and introduce significant instability into the optimization process. In this paper, we seek to resolve these issues from the perspective of optimizer design. Unlike prior TTA using manually designed optimizers like SGD, we employ a learning-to-optimize approach to automatically learn an optimizer, called Meta Gradient Generator (MGG). Specifically, we aim for MGG to effectively utilize historical gradient information during the online optimization process to optimize the current model. To this end, in MGG, we design a lightweight and efficient sequence modeling layer -- gradient memory layer. It exploits a self-supervised reconstruction loss to compress historical gradient information into network parameters, thereby enabling better memorization ability over a long-term adaptation process. We only need a small number of unlabeled samples to pre-train MGG, and then the trained MGG can be deployed to process unseen samples. Promising results on ImageNet-C, R, Sketch, and A indicate that our method surpasses current state-of-the-art methods with fewer updates, less data, and significantly shorter adaptation iterations. Compared with a previous SOTA method SAR, we achieve 7.4% accuracy improvement and 4.2 times faster adaptation speed on ImageNet-C.

Spatio-temporal Causal Learning for Streamflow Forecasting

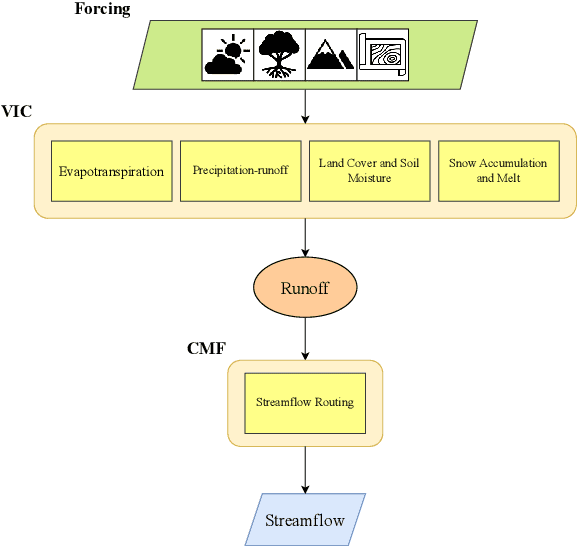
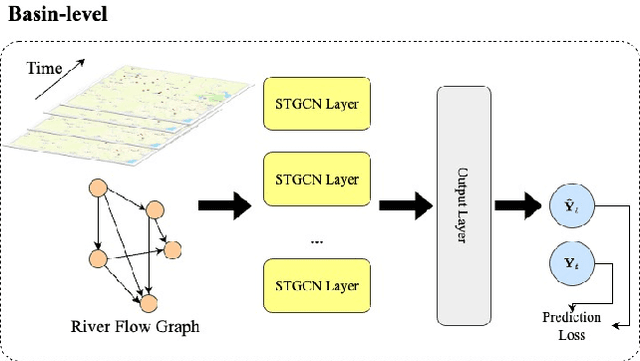
Streamflow plays an essential role in the sustainable planning and management of national water resources. Traditional hydrologic modeling approaches simulate streamflow by establishing connections across multiple physical processes, such as rainfall and runoff. These data, inherently connected both spatially and temporally, possess intrinsic causal relations that can be leveraged for robust and accurate forecasting. Recently, spatio-temporal graph neural networks (STGNNs) have been adopted, excelling in various domains, such as urban traffic management, weather forecasting, and pandemic control, and they also promise advances in streamflow management. However, learning causal relationships directly from vast observational data is theoretically and computationally challenging. In this study, we employ a river flow graph as prior knowledge to facilitate the learning of the causal structure and then use the learned causal graph to predict streamflow at targeted sites. The proposed model, Causal Streamflow Forecasting (CSF) is tested in a real-world study in the Brazos River basin in Texas. Our results demonstrate that our method outperforms regular spatio-temporal graph neural networks and achieves higher computational efficiency compared to traditional simulation methods. By effectively integrating river flow graphs with STGNNs, this research offers a novel approach to streamflow prediction, showcasing the potential of combining advanced neural network techniques with domain-specific knowledge for enhanced performance in hydrologic modeling.

Solving the Food-Energy-Water Nexus Problem via Intelligent Optimization Algorithms

The application of evolutionary algorithms (EAs) to multi-objective optimization problems has been widespread. However, the EA research community has not paid much attention to large-scale multi-objective optimization problems arising from real-world applications. Especially, Food-Energy-Water systems are intricately linked among food, energy and water that impact each other. They usually involve a huge number of decision variables and many conflicting objectives to be optimized. Solving their related optimization problems is essentially important to sustain the high-quality life of human beings. Their solution space size expands exponentially with the number of decision variables. Searching in such a vast space is challenging because of such large numbers of decision variables and objective functions. In recent years, a number of large-scale many-objectives optimization evolutionary algorithms have been proposed. In this paper, we solve a Food-Energy-Water optimization problem by using the state-of-art intelligent optimization methods and compare their performance. Our results conclude that the algorithm based on an inverse model outperforms the others. This work should be highly useful for practitioners to select the most suitable method for their particular large-scale engineering optimization problems.

Stochastic Weakly Convex Optimization Beyond Lipschitz Continuity

This paper considers stochastic weakly convex optimization without the standard Lipschitz continuity assumption. Based on new adaptive regularization (stepsize) strategies, we show that a wide class of stochastic algorithms, including the stochastic subgradient method, preserve the $\mathcal{O} ( 1 / \sqrt{K})$ convergence rate with constant failure rate. Our analyses rest on rather weak assumptions: the Lipschitz parameter can be either bounded by a general growth function of $\|x\|$ or locally estimated through independent random samples.

A Homogenization Approach for Gradient-Dominated Stochastic Optimization

Gradient dominance property is a condition weaker than strong convexity, yet it sufficiently ensures global convergence for first-order methods even in non-convex optimization. This property finds application in various machine learning domains, including matrix decomposition, linear neural networks, and policy-based reinforcement learning (RL). In this paper, we study the stochastic homogeneous second-order descent method (SHSODM) for gradient-dominated optimization with $\alpha \in [1, 2]$ based on a recently proposed homogenization approach. Theoretically, we show that SHSODM achieves a sample complexity of $O(\epsilon^{-7/(2 \alpha) +1})$ for $\alpha \in [1, 3/2)$ and $\tilde{O}(\epsilon^{-2/\alpha})$ for $\alpha \in [3/2, 2]$. We further provide a SHSODM with a variance reduction technique enjoying an improved sample complexity of $O( \epsilon ^{-( 7-3\alpha ) /( 2\alpha )})$ for $\alpha \in [1,3/2)$. Our results match the state-of-the-art sample complexity bounds for stochastic gradient-dominated optimization without \emph{cubic regularization}. Since the homogenization approach only relies on solving extremal eigenvector problems instead of Newton-type systems, our methods gain the advantage of cheaper iterations and robustness in ill-conditioned problems. Numerical experiments on several RL tasks demonstrate the efficiency of SHSODM compared to other off-the-shelf methods.

GBM-based Bregman Proximal Algorithms for Constrained Learning

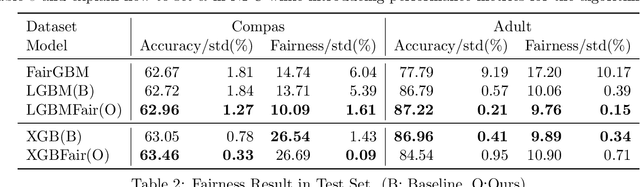
As the complexity of learning tasks surges, modern machine learning encounters a new constrained learning paradigm characterized by more intricate and data-driven function constraints. Prominent applications include Neyman-Pearson classification (NPC) and fairness classification, which entail specific risk constraints that render standard projection-based training algorithms unsuitable. Gradient boosting machines (GBMs) are among the most popular algorithms for supervised learning; however, they are generally limited to unconstrained settings. In this paper, we adapt the GBM for constrained learning tasks within the framework of Bregman proximal algorithms. We introduce a new Bregman primal-dual method with a global optimality guarantee when the learning objective and constraint functions are convex. In cases of nonconvex functions, we demonstrate how our algorithm remains effective under a Bregman proximal point framework. Distinct from existing constrained learning algorithms, ours possess a unique advantage in their ability to seamlessly integrate with publicly available GBM implementations such as XGBoost (Chen and Guestrin, 2016) and LightGBM (Ke et al., 2017), exclusively relying on their public interfaces. We provide substantial experimental evidence to showcase the effectiveness of the Bregman algorithm framework. While our primary focus is on NPC and fairness ML, our framework holds significant potential for a broader range of constrained learning applications. The source code is currently freely available at https://github.com/zhenweilin/ConstrainedGBM}{https://github.com/zhenweilin/ConstrainedGBM.

First-order methods for Stochastic Variational Inequality problems with Function Constraints

The monotone Variational Inequality (VI) is an important problem in machine learning. In numerous instances, the VI problems are accompanied by function constraints which can possibly be data-driven, making the projection operator challenging to compute. In this paper, we present novel first-order methods for function constrained VI (FCVI) problem under various settings, including smooth or nonsmooth problems with a stochastic operator and/or stochastic constraints. First, we introduce the~{\texttt{OpConEx}} method and its stochastic variants, which employ extrapolation of the operator and constraint evaluations to update the variables and the Lagrangian multipliers. These methods achieve optimal operator or sample complexities when the FCVI problem is either (i) deterministic nonsmooth, or (ii) stochastic, including smooth or nonsmooth stochastic constraints. Notably, our algorithms are simple single-loop procedures and do not require the knowledge of Lagrange multipliers to attain these complexities. Second, to obtain the optimal operator complexity for smooth deterministic problems, we present a novel single-loop Adaptive Lagrangian Extrapolation~(\texttt{AdLagEx}) method that can adaptively search for and explicitly bound the Lagrange multipliers. Furthermore, we show that all of our algorithms can be easily extended to saddle point problems with coupled function constraints, hence achieving similar complexity results for the aforementioned cases. To our best knowledge, many of these complexities are obtained for the first time in the literature.

Stochastic Dimension-reduced Second-order Methods for Policy Optimization

In this paper, we propose several new stochastic second-order algorithms for policy optimization that only require gradient and Hessian-vector product in each iteration, making them computationally efficient and comparable to policy gradient methods. Specifically, we propose a dimension-reduced second-order method (DR-SOPO) which repeatedly solves a projected two-dimensional trust region subproblem. We show that DR-SOPO obtains an $\mathcal{O}(\epsilon^{-3.5})$ complexity for reaching approximate first-order stationary condition and certain subspace second-order stationary condition. In addition, we present an enhanced algorithm (DVR-SOPO) which further improves the complexity to $\mathcal{O}(\epsilon^{-3})$ based on the variance reduction technique. Preliminary experiments show that our proposed algorithms perform favorably compared with stochastic and variance-reduced policy gradient methods.

Efficient First-order Methods for Convex Optimization with Strongly Convex Function Constraints

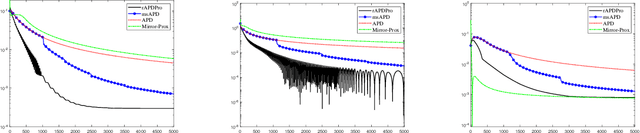
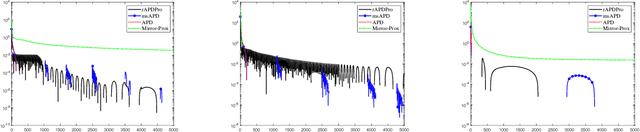
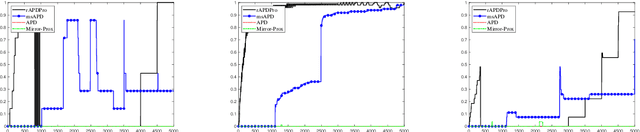
Convex function constrained optimization has received growing research interests lately. For a special convex problem which has strongly convex function constraints, we develop a new accelerated primal-dual first-order method that obtains an $\Ocal(1/\sqrt{\vep})$ complexity bound, improving the $\Ocal(1/{\vep})$ result for the state-of-the-art first-order methods. The key ingredient to our development is some novel techniques to progressively estimate the strong convexity of the Lagrangian function, which enables adaptive step-size selection and faster convergence performance. In addition, we show that the complexity is further improvable in terms of the dependence on some problem parameter, via a restart scheme that calls the accelerated method repeatedly. As an application, we consider sparsity-inducing constrained optimization which has a separable convex objective and a strongly convex loss constraint. In addition to achieving fast convergence, we show that the restarted method can effectively identify the sparsity pattern (active-set) of the optimal solution in finite steps. To the best of our knowledge, this is the first active-set identification result for sparsity-inducing constrained optimization.