Efficient First-order Methods for Convex Optimization with Strongly Convex Function Constraints
Paper and Code
Dec 26, 2022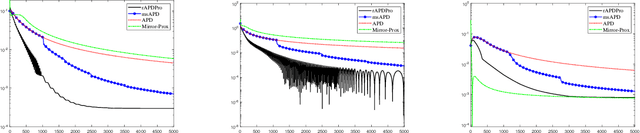
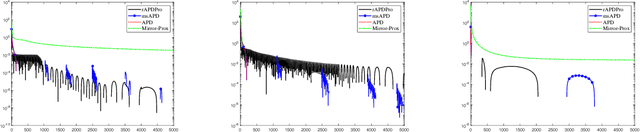
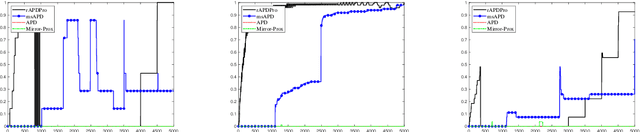
Convex function constrained optimization has received growing research interests lately. For a special convex problem which has strongly convex function constraints, we develop a new accelerated primal-dual first-order method that obtains an $\Ocal(1/\sqrt{\vep})$ complexity bound, improving the $\Ocal(1/{\vep})$ result for the state-of-the-art first-order methods. The key ingredient to our development is some novel techniques to progressively estimate the strong convexity of the Lagrangian function, which enables adaptive step-size selection and faster convergence performance. In addition, we show that the complexity is further improvable in terms of the dependence on some problem parameter, via a restart scheme that calls the accelerated method repeatedly. As an application, we consider sparsity-inducing constrained optimization which has a separable convex objective and a strongly convex loss constraint. In addition to achieving fast convergence, we show that the restarted method can effectively identify the sparsity pattern (active-set) of the optimal solution in finite steps. To the best of our knowledge, this is the first active-set identification result for sparsity-inducing constrained optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge