GBM-based Bregman Proximal Algorithms for Constrained Learning

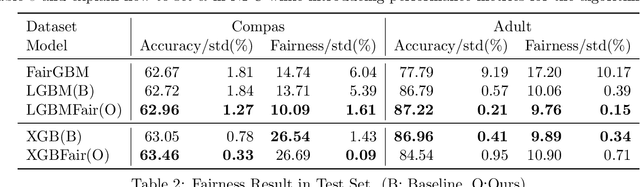
As the complexity of learning tasks surges, modern machine learning encounters a new constrained learning paradigm characterized by more intricate and data-driven function constraints. Prominent applications include Neyman-Pearson classification (NPC) and fairness classification, which entail specific risk constraints that render standard projection-based training algorithms unsuitable. Gradient boosting machines (GBMs) are among the most popular algorithms for supervised learning; however, they are generally limited to unconstrained settings. In this paper, we adapt the GBM for constrained learning tasks within the framework of Bregman proximal algorithms. We introduce a new Bregman primal-dual method with a global optimality guarantee when the learning objective and constraint functions are convex. In cases of nonconvex functions, we demonstrate how our algorithm remains effective under a Bregman proximal point framework. Distinct from existing constrained learning algorithms, ours possess a unique advantage in their ability to seamlessly integrate with publicly available GBM implementations such as XGBoost (Chen and Guestrin, 2016) and LightGBM (Ke et al., 2017), exclusively relying on their public interfaces. We provide substantial experimental evidence to showcase the effectiveness of the Bregman algorithm framework. While our primary focus is on NPC and fairness ML, our framework holds significant potential for a broader range of constrained learning applications. The source code is currently freely available at https://github.com/zhenweilin/ConstrainedGBM}{https://github.com/zhenweilin/ConstrainedGBM.

Efficient First-order Methods for Convex Optimization with Strongly Convex Function Constraints

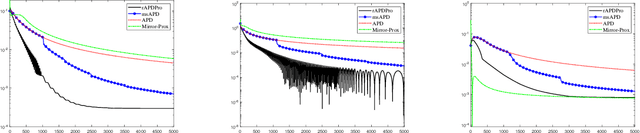
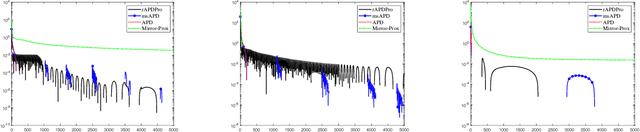
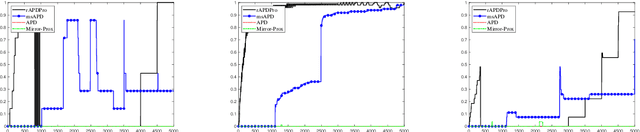
Convex function constrained optimization has received growing research interests lately. For a special convex problem which has strongly convex function constraints, we develop a new accelerated primal-dual first-order method that obtains an $\Ocal(1/\sqrt{\vep})$ complexity bound, improving the $\Ocal(1/{\vep})$ result for the state-of-the-art first-order methods. The key ingredient to our development is some novel techniques to progressively estimate the strong convexity of the Lagrangian function, which enables adaptive step-size selection and faster convergence performance. In addition, we show that the complexity is further improvable in terms of the dependence on some problem parameter, via a restart scheme that calls the accelerated method repeatedly. As an application, we consider sparsity-inducing constrained optimization which has a separable convex objective and a strongly convex loss constraint. In addition to achieving fast convergence, we show that the restarted method can effectively identify the sparsity pattern (active-set) of the optimal solution in finite steps. To the best of our knowledge, this is the first active-set identification result for sparsity-inducing constrained optimization.