Digvijay Boob
First-order methods for Stochastic Variational Inequality problems with Function Constraints
Apr 21, 2023
Abstract:The monotone Variational Inequality (VI) is an important problem in machine learning. In numerous instances, the VI problems are accompanied by function constraints which can possibly be data-driven, making the projection operator challenging to compute. In this paper, we present novel first-order methods for function constrained VI (FCVI) problem under various settings, including smooth or nonsmooth problems with a stochastic operator and/or stochastic constraints. First, we introduce the~{\texttt{OpConEx}} method and its stochastic variants, which employ extrapolation of the operator and constraint evaluations to update the variables and the Lagrangian multipliers. These methods achieve optimal operator or sample complexities when the FCVI problem is either (i) deterministic nonsmooth, or (ii) stochastic, including smooth or nonsmooth stochastic constraints. Notably, our algorithms are simple single-loop procedures and do not require the knowledge of Lagrange multipliers to attain these complexities. Second, to obtain the optimal operator complexity for smooth deterministic problems, we present a novel single-loop Adaptive Lagrangian Extrapolation~(\texttt{AdLagEx}) method that can adaptively search for and explicitly bound the Lagrange multipliers. Furthermore, we show that all of our algorithms can be easily extended to saddle point problems with coupled function constraints, hence achieving similar complexity results for the aforementioned cases. To our best knowledge, many of these complexities are obtained for the first time in the literature.
Accelerated Primal-Dual Methods for Convex-Strongly-Concave Saddle Point Problems
Sep 10, 2022
Abstract:In this work, we aim to investigate Primal-Dual (PD) methods for convex-strongly-concave saddle point problems (SPP). In many cases, the computation of the proximal oracle over the primal-only function is inefficient. Hence, we use its first-order linear approximation in the proximal step resulting in a Linearized PD (LPD) method. Even when the coupling term is bilinear, we observe that LPD has a suboptimal dependence on the Lipschitz constant of the primal-only function. In contrast, LPD has optimal convergence for the strongly-convex concave case. This observation induces us to present our accelerated linearized primal-dual (ALPD) algorithm to solve convex strongly-concave SPP. ALPD is a single-loop algorithm that combines features of Nesterov's accelerated gradient descent (AGD) and LPD. We show that when the coupling term is semi-linear (which contains bilinear as a specific case), ALPD obtains the optimal dependence on the Lipschitz constant of primal-only function. Hence, it is an optimal algorithm. When the coupling term has a general nonlinear form, the ALPD algorithm has suboptimal dependence on the Lipschitz constant of the primal part of the coupling term. To improve this dependence, we present an inexact APD algorithm. This algorithm performs AGD iterations in the inner loop to find an approximate solution to a proximal subproblem of APD. We show that inexact APD maintains optimal number of gradients evaluations (gradient complexity) of primal-only and dual parts of the problem. It also significantly improves the gradient-complexity of the primal coupling term.
Optimal Algorithms for Differentially Private Stochastic Monotone Variational Inequalities and Saddle-Point Problems
Apr 07, 2021
Abstract:In this work, we conduct the first systematic study of stochastic variational inequality (SVI) and stochastic saddle point (SSP) problems under the constraint of differential privacy-(DP). We propose two algorithms: Noisy Stochastic Extragradient (NSEG) and Noisy Inexact Stochastic Proximal Point (NISPP). We show that sampling with replacement variants of these algorithms attain the optimal risk for DP-SVI and DP-SSP. Key to our analysis is the investigation of algorithmic stability bounds, both of which are new even in the nonprivate case, together with a novel "stability implies generalization" result for the gap functions for SVI and SSP problems. The dependence of the running time of these algorithms, with respect to the dataset size $n$, is $n^2$ for NSEG and $\widetilde{O}(n^{3/2})$ for NISPP.
A Feasible Level Proximal Point Method for Nonconvex Sparse Constrained Optimization
Oct 23, 2020



Abstract:Nonconvex sparse models have received significant attention in high-dimensional machine learning. In this paper, we study a new model consisting of a general convex or nonconvex objectives and a variety of continuous nonconvex sparsity-inducing constraints. For this constrained model, we propose a novel proximal point algorithm that solves a sequence of convex subproblems with gradually relaxed constraint levels. Each subproblem, having a proximal point objective and a convex surrogate constraint, can be efficiently solved based on a fast routine for projection onto the surrogate constraint. We establish the asymptotic convergence of the proposed algorithm to the Karush-Kuhn-Tucker (KKT) solutions. We also establish new convergence complexities to achieve an approximate KKT solution when the objective can be smooth/nonsmooth, deterministic/stochastic and convex/nonconvex with complexity that is on a par with gradient descent for unconstrained optimization problems in respective cases. To the best of our knowledge, this is the first study of the first-order methods with complexity guarantee for nonconvex sparse-constrained problems. We perform numerical experiments to demonstrate the effectiveness of our new model and efficiency of the proposed algorithm for large scale problems.
Differentially Private Mixed-Type Data Generation For Unsupervised Learning
Dec 06, 2019



Abstract:In this work we introduce the DP-auto-GAN framework for synthetic data generation, which combines the low dimensional representation of autoencoders with the flexibility of Generative Adversarial Networks (GANs). This framework can be used to take in raw sensitive data, and privately train a model for generating synthetic data that will satisfy the same statistical properties as the original data. This learned model can be used to generate arbitrary amounts of publicly available synthetic data, which can then be freely shared due to the post-processing guarantees of differential privacy. Our framework is applicable to unlabeled mixed-type data, that may include binary, categorical, and real-valued data. We implement this framework on both unlabeled binary data (MIMIC-III) and unlabeled mixed-type data (ADULT). We also introduce new metrics for evaluating the quality of synthetic mixed-type data, particularly in unsupervised settings.
Faster width-dependent algorithm for mixed packing and covering LPs
Sep 26, 2019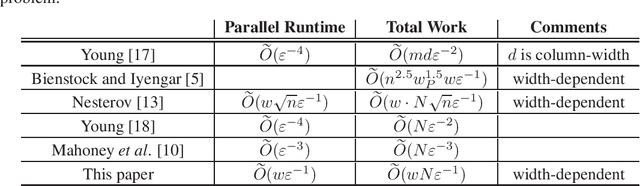
Abstract:In this paper, we give a faster width-dependent algorithm for mixed packing-covering LPs. Mixed packing-covering LPs are fundamental to combinatorial optimization in computer science and operations research. Our algorithm finds a $1+\eps$ approximate solution in time $O(Nw/ \eps)$, where $N$ is number of nonzero entries in the constraint matrix and $w$ is the maximum number of nonzeros in any constraint. This run-time is better than Nesterov's smoothing algorithm which requires $O(N\sqrt{n}w/ \eps)$ where $n$ is the dimension of the problem. Our work utilizes the framework of area convexity introduced in [Sherman-FOCS'17] to obtain the best dependence on $\eps$ while breaking the infamous $\ell_{\infty}$ barrier to eliminate the factor of $\sqrt{n}$. The current best width-independent algorithm for this problem runs in time $O(N/\eps^2)$ [Young-arXiv-14] and hence has worse running time dependence on $\eps$. Many real life instances of the mixed packing-covering problems exhibit small width and for such cases, our algorithm can report higher precision results when compared to width-independent algorithms. As a special case of our result, we report a $1+\eps$ approximation algorithm for the densest subgraph problem which runs in time $O(md/ \eps)$, where $m$ is the number of edges in the graph and $d$ is the maximum graph degree.
Proximal Point Methods for Optimization with Nonconvex Functional Constraints
Aug 07, 2019Abstract:Nonconvex optimization is becoming more and more important in machine learning and operations research. In spite of recent progresses, the development of provably efficient algorithm for optimization with nonconvex functional constraints remains open. Such problems have potential applications in risk-averse machine learning, semisupervised learning and robust optimization among others. In this paper, we introduce a new proximal point type method for solving this important class of nonconvex problems by transforming them into a sequence of convex constrained subproblems. We establish the convergence and rate of convergence of this algorithm to the KKT point under different types of constraint qualifications. In particular, we prove that our algorithm will converge to an $\epsilon$-KKT point in $O(1/\epsilon)$ iterations under a properly defined condition. For practical use, we present inexact variants of this approach, in which approximate solutions of the subproblems are computed by either primal or primal-dual type algorithms, and establish their associated rate of convergence. To the best of our knowledge, this is the first time that proximal point type method is developed for nonlinear programing with nonconvex functional constraints, and most of the convergence and complexity results seem to be new in the literature.
Complexity of Training ReLU Neural Network
Sep 27, 2018



Abstract:In this paper, we explore some basic questions on the complexity of training Neural networks with ReLU activation function. We show that it is NP-hard to train a two- hidden layer feedforward ReLU neural network. If dimension d of the data is fixed then we show that there exists a polynomial time algorithm for the same training problem. We also show that if sufficient over-parameterization is provided in the first hidden layer of ReLU neural network then there is a polynomial time algorithm which finds weights such that output of the over-parameterized ReLU neural network matches with the output of the given data
Theoretical properties of the global optimizer of two layer neural network
Oct 30, 2017Abstract:In this paper, we study the problem of optimizing a two-layer artificial neural network that best fits a training dataset. We look at this problem in the setting where the number of parameters is greater than the number of sampled points. We show that for a wide class of differentiable activation functions (this class involves "almost" all functions which are not piecewise linear), we have that first-order optimal solutions satisfy global optimality provided the hidden layer is non-singular. Our results are easily extended to hidden layers given by a flat matrix from that of a square matrix. Results are applicable even if network has more than one hidden layer provided all hidden layers satisfy non-singularity, all activations are from the given "good" class of differentiable functions and optimization is only with respect to the last hidden layer. We also study the smoothness properties of the objective function and show that it is actually Lipschitz smooth, i.e., its gradients do not change sharply. We use smoothness properties to guarantee asymptotic convergence of O(1/number of iterations) to a first-order optimal solution. We also show that our algorithm will maintain non-singularity of hidden layer for any finite number of iterations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge