Faster width-dependent algorithm for mixed packing and covering LPs
Paper and Code
Sep 26, 2019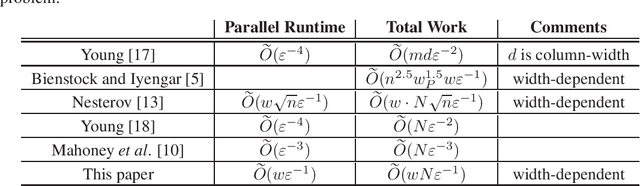
In this paper, we give a faster width-dependent algorithm for mixed packing-covering LPs. Mixed packing-covering LPs are fundamental to combinatorial optimization in computer science and operations research. Our algorithm finds a $1+\eps$ approximate solution in time $O(Nw/ \eps)$, where $N$ is number of nonzero entries in the constraint matrix and $w$ is the maximum number of nonzeros in any constraint. This run-time is better than Nesterov's smoothing algorithm which requires $O(N\sqrt{n}w/ \eps)$ where $n$ is the dimension of the problem. Our work utilizes the framework of area convexity introduced in [Sherman-FOCS'17] to obtain the best dependence on $\eps$ while breaking the infamous $\ell_{\infty}$ barrier to eliminate the factor of $\sqrt{n}$. The current best width-independent algorithm for this problem runs in time $O(N/\eps^2)$ [Young-arXiv-14] and hence has worse running time dependence on $\eps$. Many real life instances of the mixed packing-covering problems exhibit small width and for such cases, our algorithm can report higher precision results when compared to width-independent algorithms. As a special case of our result, we report a $1+\eps$ approximation algorithm for the densest subgraph problem which runs in time $O(md/ \eps)$, where $m$ is the number of edges in the graph and $d$ is the maximum graph degree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge