Measuring Disparate Outcomes of Content Recommendation Algorithms with Distributional Inequality Metrics

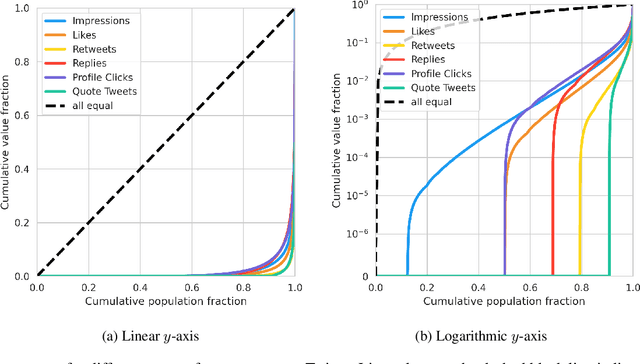
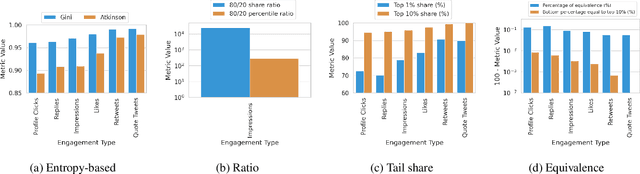
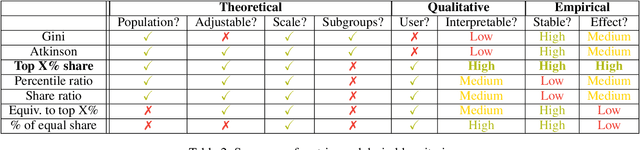
The harmful impacts of algorithmic decision systems have recently come into focus, with many examples of systems such as machine learning (ML) models amplifying existing societal biases. Most metrics attempting to quantify disparities resulting from ML algorithms focus on differences between groups, dividing users based on demographic identities and comparing model performance or overall outcomes between these groups. However, in industry settings, such information is often not available, and inferring these characteristics carries its own risks and biases. Moreover, typical metrics that focus on a single classifier's output ignore the complex network of systems that produce outcomes in real-world settings. In this paper, we evaluate a set of metrics originating from economics, distributional inequality metrics, and their ability to measure disparities in content exposure in a production recommendation system, the Twitter algorithmic timeline. We define desirable criteria for metrics to be used in an operational setting, specifically by ML practitioners. We characterize different types of engagement with content on Twitter using these metrics, and use these results to evaluate the metrics with respect to the desired criteria. We show that we can use these metrics to identify content suggestion algorithms that contribute more strongly to skewed outcomes between users. Overall, we conclude that these metrics can be useful tools for understanding disparate outcomes in online social networks.

Image Cropping on Twitter: Fairness Metrics, their Limitations, and the Importance of Representation, Design, and Agency

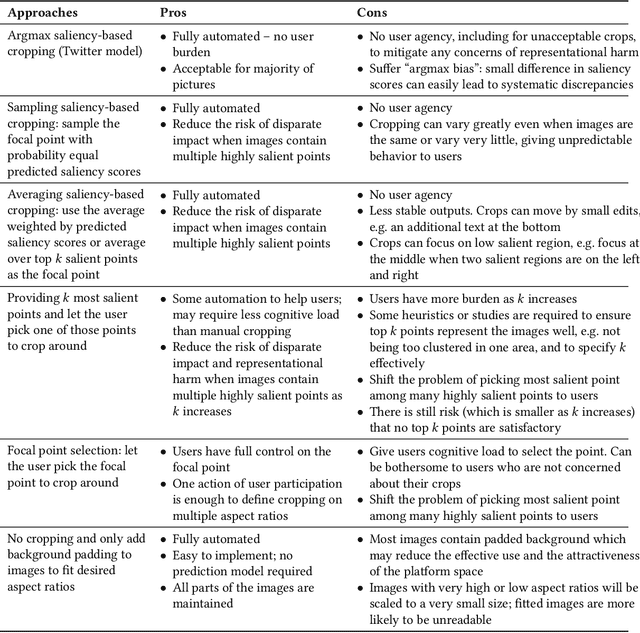
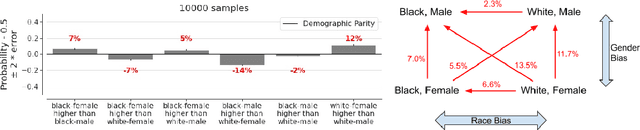
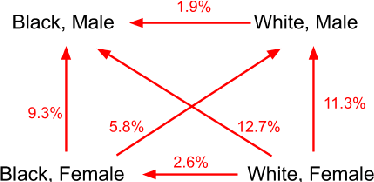
Twitter uses machine learning to crop images, where crops are centered around the part predicted to be the most salient. In fall 2020, Twitter users raised concerns that the automated image cropping system on Twitter favored light-skinned over dark-skinned individuals, as well as concerns that the system favored cropping woman's bodies instead of their heads. In order to address these concerns, we conduct an extensive analysis using formalized group fairness metrics. We find systematic disparities in cropping and identify contributing factors, including the fact that the cropping based on the single most salient point can amplify the disparities. However, we demonstrate that formalized fairness metrics and quantitative analysis on their own are insufficient for capturing the risk of representational harm in automatic cropping. We suggest the removal of saliency-based cropping in favor of a solution that better preserves user agency. For developing a new solution that sufficiently address concerns related to representational harm, our critique motivates a combination of quantitative and qualitative methods that include human-centered design.

Fast and Memory Efficient Differentially Private-SGD via JL Projections

Differentially Private-SGD (DP-SGD) of Abadi et al. (2016) and its variations are the only known algorithms for private training of large scale neural networks. This algorithm requires computation of per-sample gradients norms which is extremely slow and memory intensive in practice. In this paper, we present a new framework to design differentially private optimizers called DP-SGD-JL and DP-Adam-JL. Our approach uses Johnson-Lindenstrauss (JL) projections to quickly approximate the per-sample gradient norms without exactly computing them, thus making the training time and memory requirements of our optimizers closer to that of their non-DP versions. Unlike previous attempts to make DP-SGD faster which work only on a subset of network architectures or use compiler techniques, we propose an algorithmic solution which works for any network in a black-box manner which is the main contribution of this paper. To illustrate this, on IMDb dataset, we train a Recurrent Neural Network (RNN) to achieve good privacy-vs-accuracy tradeoff, while being significantly faster than DP-SGD and with a similar memory footprint as non-private SGD. The privacy analysis of our algorithms is more involved than DP-SGD, we use the recently proposed f-DP framework of Dong et al. (2019) to prove privacy.

$λ$-Regularized A-Optimal Design and its Approximation by $λ$-Regularized Proportional Volume Sampling

In this work, we study the $\lambda$-regularized $A$-optimal design problem and introduce the $\lambda$-regularized proportional volume sampling algorithm, generalized from [Nikolov, Singh, and Tantipongpipat, 2019], for this problem with the approximation guarantee that extends upon the previous work. In this problem, we are given vectors $v_1,\ldots,v_n\in\mathbb{R}^d$ in $d$ dimensions, a budget $k\leq n$, and the regularizer parameter $\lambda\geq0$, and the goal is to find a subset $S\subseteq [n]$ of size $k$ that minimizes the trace of $\left(\sum_{i\in S}v_iv_i^\top + \lambda I_d\right)^{-1}$ where $I_d$ is the $d\times d$ identity matrix. The problem is motivated from optimal design in ridge regression, where one tries to minimize the expected squared error of the ridge regression predictor from the true coefficient in the underlying linear model. We introduce $\lambda$-regularized proportional volume sampling and give its polynomial-time implementation to solve this problem. We show its $(1+\frac{\epsilon}{\sqrt{1+\lambda'}})$-approximation for $k=\Omega\left(\frac d\epsilon+\frac{\log 1/\epsilon}{\epsilon^2}\right)$ where $\lambda'$ is proportional to $\lambda$, extending the previous bound in [Nikolov, Singh, and Tantipongpipat, 2019] to the case $\lambda>0$ and obtaining asymptotic optimality as $\lambda\rightarrow \infty$.

Maximizing Determinants under Matroid Constraints

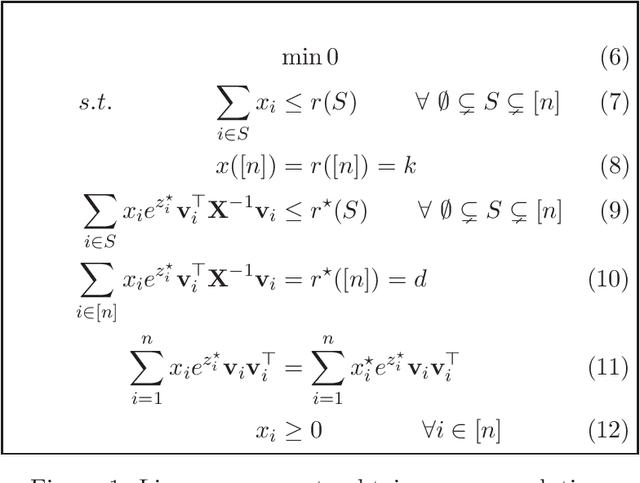
Given vectors $v_1,\dots,v_n\in\mathbb{R}^d$ and a matroid $M=([n],I)$, we study the problem of finding a basis $S$ of $M$ such that $\det(\sum_{i \in S}v_i v_i^\top)$ is maximized. This problem appears in a diverse set of areas such as experimental design, fair allocation of goods, network design, and machine learning. The current best results include an $e^{2k}$-estimation for any matroid of rank $k$ and a $(1+\epsilon)^d$-approximation for a uniform matroid of rank $k\ge d+\frac d\epsilon$, where the rank $k\ge d$ denotes the desired size of the optimal set. Our main result is a new approximation algorithm with an approximation guarantee that depends only on the dimension $d$ of the vectors and not on the size $k$ of the output set. In particular, we show an $(O(d))^{d}$-estimation and an $(O(d))^{d^3}$-approximation for any matroid, giving a significant improvement over prior work when $k\gg d$. Our result relies on the existence of an optimal solution to a convex programming relaxation for the problem which has sparse support; in particular, no more than $O(d^2)$ variables of the solution have fractional values. The sparsity results rely on the interplay between the first-order optimality conditions for the convex program and matroid theory. We believe that the techniques introduced to show sparsity of optimal solutions to convex programs will be of independent interest. We also give a randomized algorithm that rounds a sparse fractional solution to a feasible integral solution to the original problem. To show the approximation guarantee, we utilize recent works on strongly log-concave polynomials and show new relationships between different convex programs studied for the problem. Finally, we use the estimation algorithm and sparsity results to give an efficient deterministic approximation algorithm with an approximation guarantee that depends solely on the dimension $d$.

Differentially Private Mixed-Type Data Generation For Unsupervised Learning

In this work we introduce the DP-auto-GAN framework for synthetic data generation, which combines the low dimensional representation of autoencoders with the flexibility of Generative Adversarial Networks (GANs). This framework can be used to take in raw sensitive data, and privately train a model for generating synthetic data that will satisfy the same statistical properties as the original data. This learned model can be used to generate arbitrary amounts of publicly available synthetic data, which can then be freely shared due to the post-processing guarantees of differential privacy. Our framework is applicable to unlabeled mixed-type data, that may include binary, categorical, and real-valued data. We implement this framework on both unlabeled binary data (MIMIC-III) and unlabeled mixed-type data (ADULT). We also introduce new metrics for evaluating the quality of synthetic mixed-type data, particularly in unsupervised settings.

Fair Dimensionality Reduction and Iterative Rounding for SDPs

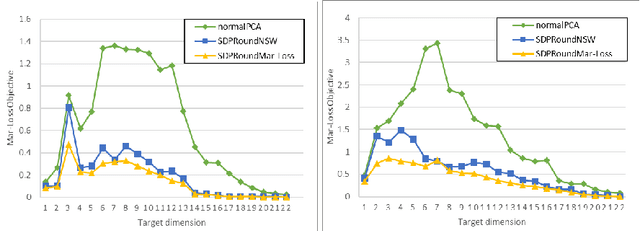
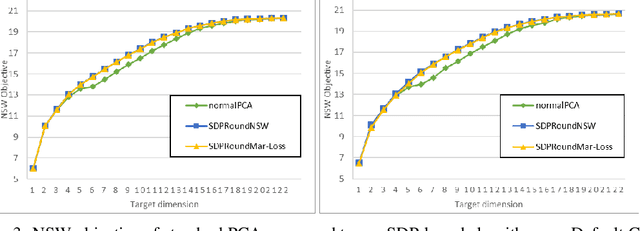
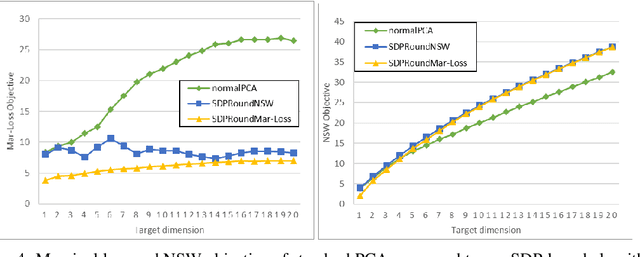
We model "fair" dimensionality reduction as an optimization problem. A central example is the fair PCA problem: the input data is divided into $k$ groups, and the goal is to find a single $d$-dimensional representation for all groups for which the maximum variance (or minimum reconstruction error) is optimized for all groups in a fair (or balanced) manner, e.g., by maximizing the minimum variance over the $k$ groups of the projection to a $d$-dimensional subspace. This problem was introduced by Samadi et al. (2018) who gave a polynomial-time algorithm which, for $k=2$ groups, returns a $(d+1)$-dimensional solution of value at least the best $d$-dimensional solution. We give an exact polynomial-time algorithm for $k=2$ groups. The result relies on extending results of Pataki (1998) regarding rank of extreme point solutions to semi-definite programs. This approach applies more generally to any monotone concave function of the individual group objectives. For $k>2$ groups, our results generalize to give a $(d+\sqrt{2k+0.25}-1.5)$-dimensional solution with objective value as good as the optimal $d$-dimensional solution for arbitrary $k,d$ in polynomial time. Using our extreme point characterization result for SDPs, we give an iterative rounding framework for general SDPs which generalizes the well-known iterative rounding approach for LPs. It returns low-rank solutions with bounded violation of constraints. We obtain a $d$-dimensional projection where the violation in the objective can be bounded additively in terms of the top $O(\sqrt{k})$-singular values of the data matrices. We also give an exact polynomial-time algorithm for any fixed number of groups and target dimension via the algorithm of Grigoriev and Pasechnik (2005). In contrast, when the number of groups is part of the input, even for target dimension $d=1$, we show this problem is NP-hard.

The Price of Fair PCA: One Extra Dimension

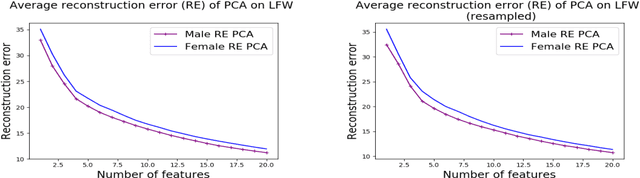
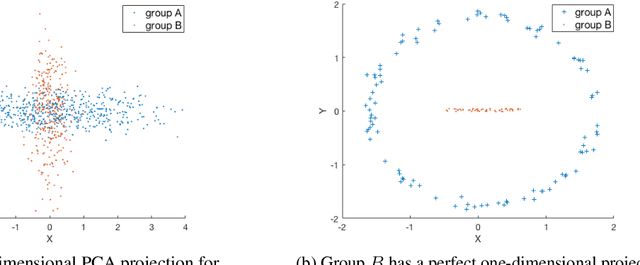
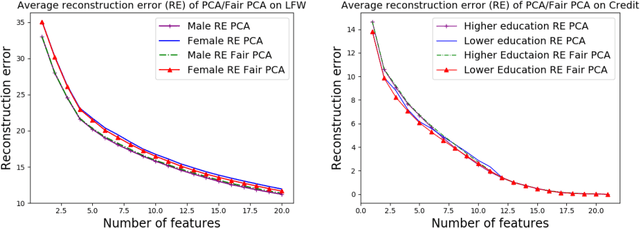
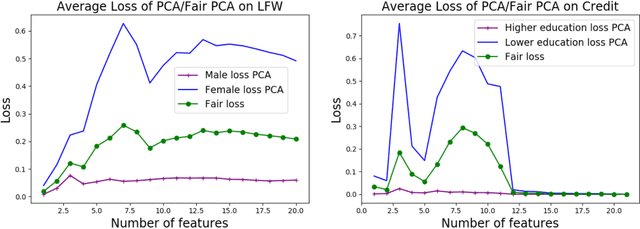
We investigate whether the standard dimensionality reduction technique of PCA inadvertently produces data representations with different fidelity for two different populations. We show on several real-world data sets, PCA has higher reconstruction error on population A than on B (for example, women versus men or lower- versus higher-educated individuals). This can happen even when the data set has a similar number of samples from A and B. This motivates our study of dimensionality reduction techniques which maintain similar fidelity for A and B. We define the notion of Fair PCA and give a polynomial-time algorithm for finding a low dimensional representation of the data which is nearly-optimal with respect to this measure. Finally, we show on real-world data sets that our algorithm can be used to efficiently generate a fair low dimensional representation of the data.