Improving language models fine-tuning with representation consistency targets

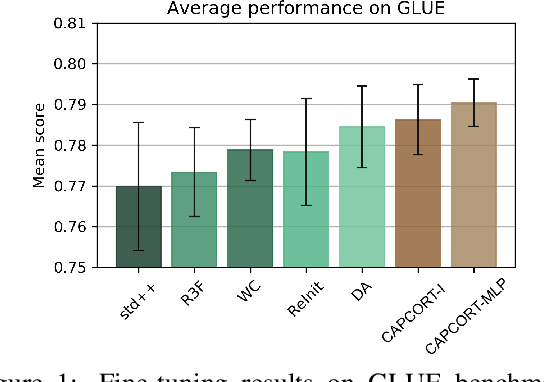
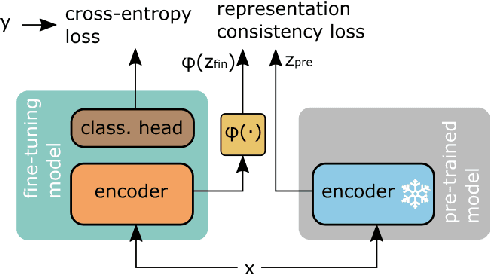
Fine-tuning contextualized representations learned by pre-trained language models has become a standard practice in the NLP field. However, pre-trained representations are prone to degradation (also known as representation collapse) during fine-tuning, which leads to instability, suboptimal performance, and weak generalization. In this paper, we propose a novel fine-tuning method that avoids representation collapse during fine-tuning by discouraging undesirable changes in the representations. We show that our approach matches or exceeds the performance of the existing regularization-based fine-tuning methods across 13 language understanding tasks (GLUE benchmark and six additional datasets). We also demonstrate its effectiveness in low-data settings and robustness to label perturbation. Furthermore, we extend previous studies of representation collapse and propose several metrics to quantify it. Using these metrics and previously proposed experiments, we show that our approach obtains significant improvements in retaining the expressive power of representations.

Improving Early Sepsis Prediction with Multi Modal Learning

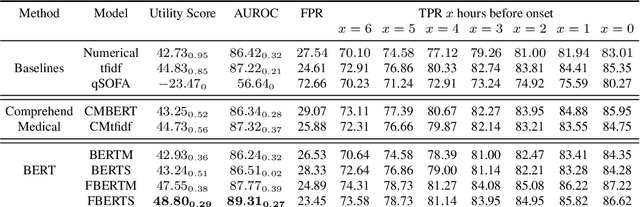
Sepsis is a life-threatening disease with high morbidity, mortality and healthcare costs. The early prediction and administration of antibiotics and intravenous fluids is considered crucial for the treatment of sepsis and can save potentially millions of lives and billions in health care costs. Professional clinical care practitioners have proposed clinical criterion which aid in early detection of sepsis; however, performance of these criterion is often limited. Clinical text provides essential information to estimate the severity of the sepsis in addition to structured clinical data. In this study, we explore how clinical text can complement structured data towards early sepsis prediction task. In this paper, we propose multi modal model which incorporates both structured data in the form of patient measurements as well as textual notes on the patient. We employ state-of-the-art NLP models such as BERT and a highly specialized NLP model in Amazon Comprehend Medical to represent the text. On the MIMIC-III dataset containing records of ICU admissions, we show that by using these notes, one achieves an improvement of 6.07 points in a standard utility score for Sepsis prediction and 2.89% in AUROC score. Our methods significantly outperforms a clinical criteria suggested by experts, qSOFA, as well as the winning model of the PhysioNet Computing in Cardiology Challenge for predicting Sepsis.

Maximizing Determinants under Matroid Constraints

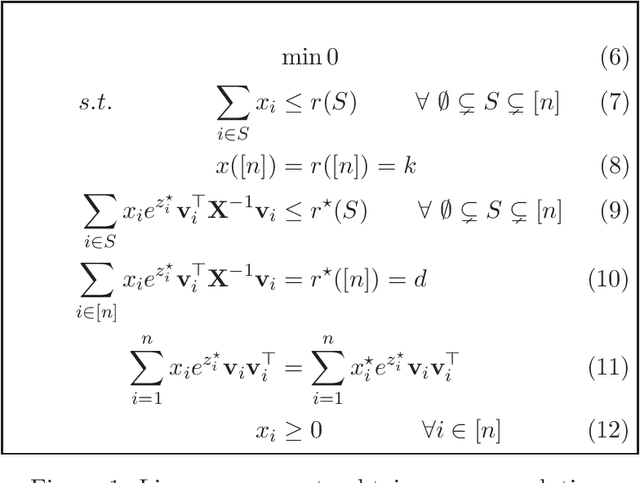
Given vectors $v_1,\dots,v_n\in\mathbb{R}^d$ and a matroid $M=([n],I)$, we study the problem of finding a basis $S$ of $M$ such that $\det(\sum_{i \in S}v_i v_i^\top)$ is maximized. This problem appears in a diverse set of areas such as experimental design, fair allocation of goods, network design, and machine learning. The current best results include an $e^{2k}$-estimation for any matroid of rank $k$ and a $(1+\epsilon)^d$-approximation for a uniform matroid of rank $k\ge d+\frac d\epsilon$, where the rank $k\ge d$ denotes the desired size of the optimal set. Our main result is a new approximation algorithm with an approximation guarantee that depends only on the dimension $d$ of the vectors and not on the size $k$ of the output set. In particular, we show an $(O(d))^{d}$-estimation and an $(O(d))^{d^3}$-approximation for any matroid, giving a significant improvement over prior work when $k\gg d$. Our result relies on the existence of an optimal solution to a convex programming relaxation for the problem which has sparse support; in particular, no more than $O(d^2)$ variables of the solution have fractional values. The sparsity results rely on the interplay between the first-order optimality conditions for the convex program and matroid theory. We believe that the techniques introduced to show sparsity of optimal solutions to convex programs will be of independent interest. We also give a randomized algorithm that rounds a sparse fractional solution to a feasible integral solution to the original problem. To show the approximation guarantee, we utilize recent works on strongly log-concave polynomials and show new relationships between different convex programs studied for the problem. Finally, we use the estimation algorithm and sparsity results to give an efficient deterministic approximation algorithm with an approximation guarantee that depends solely on the dimension $d$.