Maximizing Determinants under Matroid Constraints

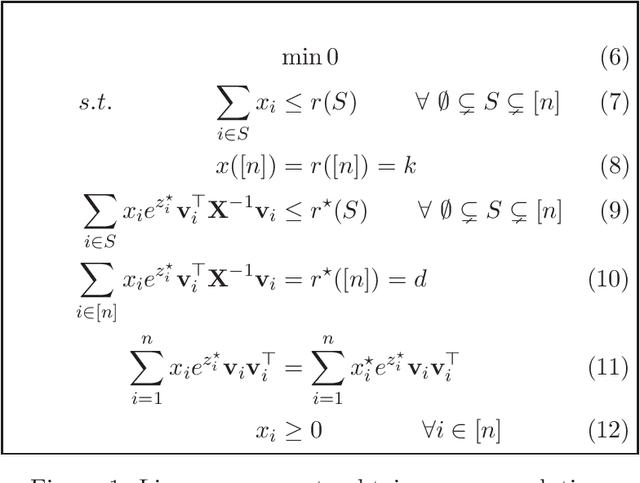
Given vectors $v_1,\dots,v_n\in\mathbb{R}^d$ and a matroid $M=([n],I)$, we study the problem of finding a basis $S$ of $M$ such that $\det(\sum_{i \in S}v_i v_i^\top)$ is maximized. This problem appears in a diverse set of areas such as experimental design, fair allocation of goods, network design, and machine learning. The current best results include an $e^{2k}$-estimation for any matroid of rank $k$ and a $(1+\epsilon)^d$-approximation for a uniform matroid of rank $k\ge d+\frac d\epsilon$, where the rank $k\ge d$ denotes the desired size of the optimal set. Our main result is a new approximation algorithm with an approximation guarantee that depends only on the dimension $d$ of the vectors and not on the size $k$ of the output set. In particular, we show an $(O(d))^{d}$-estimation and an $(O(d))^{d^3}$-approximation for any matroid, giving a significant improvement over prior work when $k\gg d$. Our result relies on the existence of an optimal solution to a convex programming relaxation for the problem which has sparse support; in particular, no more than $O(d^2)$ variables of the solution have fractional values. The sparsity results rely on the interplay between the first-order optimality conditions for the convex program and matroid theory. We believe that the techniques introduced to show sparsity of optimal solutions to convex programs will be of independent interest. We also give a randomized algorithm that rounds a sparse fractional solution to a feasible integral solution to the original problem. To show the approximation guarantee, we utilize recent works on strongly log-concave polynomials and show new relationships between different convex programs studied for the problem. Finally, we use the estimation algorithm and sparsity results to give an efficient deterministic approximation algorithm with an approximation guarantee that depends solely on the dimension $d$.