Gaussian Noise is Nearly Instance Optimal for Private Unbiased Mean Estimation

We investigate unbiased high-dimensional mean estimators in differential privacy. We consider differentially private mechanisms whose expected output equals the mean of the input dataset, for every dataset drawn from a fixed convex domain $K$ in $\mathbb{R}^d$. In the setting of concentrated differential privacy, we show that, for every input such an unbiased mean estimator introduces approximately at least as much error as a mechanism that adds Gaussian noise with a carefully chosen covariance. This is true when the error is measured with respect to $\ell_p$ error for any $p \ge 2$. We extend this result to local differential privacy, and to approximate differential privacy, but for the latter the error lower bound holds either for a dataset or for a neighboring dataset. We also extend our results to mechanisms that take i.i.d.~samples from a distribution over $K$ and are unbiased with respect to the mean of the distribution.

Learning versus Refutation in Noninteractive Local Differential Privacy

We study two basic statistical tasks in non-interactive local differential privacy (LDP): learning and refutation. Learning requires finding a concept that best fits an unknown target function (from labelled samples drawn from a distribution), whereas refutation requires distinguishing between data distributions that are well-correlated with some concept in the class, versus distributions where the labels are random. Our main result is a complete characterization of the sample complexity of agnostic PAC learning for non-interactive LDP protocols. We show that the optimal sample complexity for any concept class is captured by the approximate $\gamma_2$~norm of a natural matrix associated with the class. Combined with previous work [Edmonds, Nikolov and Ullman, 2019] this gives an equivalence between learning and refutation in the agnostic setting.

Private Query Release via the Johnson-Lindenstrauss Transform

We introduce a new method for releasing answers to statistical queries with differential privacy, based on the Johnson-Lindenstrauss lemma. The key idea is to randomly project the query answers to a lower dimensional space so that the distance between any two vectors of feasible query answers is preserved up to an additive error. Then we answer the projected queries using a simple noise-adding mechanism, and lift the answers up to the original dimension. Using this method, we give, for the first time, purely differentially private mechanisms with optimal worst case sample complexity under average error for answering a workload of $k$ queries over a universe of size $N$. As other applications, we give the first purely private efficient mechanisms with optimal sample complexity for computing the covariance of a bounded high-dimensional distribution, and for answering 2-way marginal queries. We also show that, up to the dependence on the error, a variant of our mechanism is nearly optimal for every given query workload.

Private Query Release Assisted by Public Data

We study the problem of differentially private query release assisted by access to public data. In this problem, the goal is to answer a large class $\mathcal{H}$ of statistical queries with error no more than $\alpha$ using a combination of public and private samples. The algorithm is required to satisfy differential privacy only with respect to the private samples. We study the limits of this task in terms of the private and public sample complexities. First, we show that we can solve the problem for any query class $\mathcal{H}$ of finite VC-dimension using only $d/\alpha$ public samples and $\sqrt{p}d^{3/2}/\alpha^2$ private samples, where $d$ and $p$ are the VC-dimension and dual VC-dimension of $\mathcal{H}$, respectively. In comparison, with only private samples, this problem cannot be solved even for simple query classes with VC-dimension one, and without any private samples, a larger public sample of size $d/\alpha^2$ is needed. Next, we give sample complexity lower bounds that exhibit tight dependence on $p$ and $\alpha$. For the class of decision stumps, we give a lower bound of $\sqrt{p}/\alpha$ on the private sample complexity whenever the public sample size is less than $1/\alpha^2$. Given our upper bounds, this shows that the dependence on $\sqrt{p}$ is necessary in the private sample complexity. We also give a lower bound of $1/\alpha$ on the public sample complexity for a broad family of query classes, which by our upper bound, is tight in $\alpha$.

Maximizing Determinants under Matroid Constraints

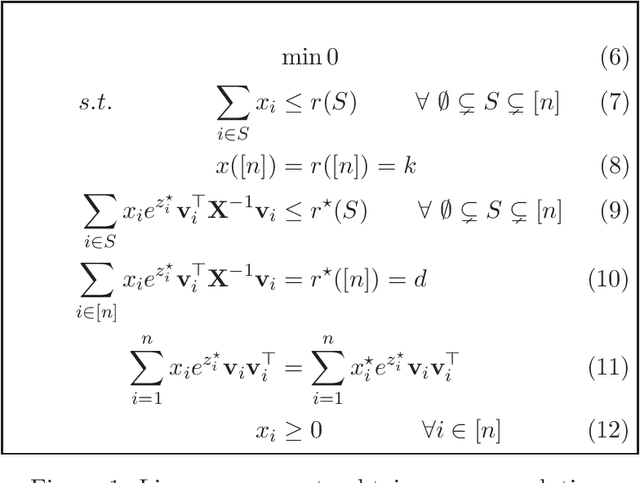
Given vectors $v_1,\dots,v_n\in\mathbb{R}^d$ and a matroid $M=([n],I)$, we study the problem of finding a basis $S$ of $M$ such that $\det(\sum_{i \in S}v_i v_i^\top)$ is maximized. This problem appears in a diverse set of areas such as experimental design, fair allocation of goods, network design, and machine learning. The current best results include an $e^{2k}$-estimation for any matroid of rank $k$ and a $(1+\epsilon)^d$-approximation for a uniform matroid of rank $k\ge d+\frac d\epsilon$, where the rank $k\ge d$ denotes the desired size of the optimal set. Our main result is a new approximation algorithm with an approximation guarantee that depends only on the dimension $d$ of the vectors and not on the size $k$ of the output set. In particular, we show an $(O(d))^{d}$-estimation and an $(O(d))^{d^3}$-approximation for any matroid, giving a significant improvement over prior work when $k\gg d$. Our result relies on the existence of an optimal solution to a convex programming relaxation for the problem which has sparse support; in particular, no more than $O(d^2)$ variables of the solution have fractional values. The sparsity results rely on the interplay between the first-order optimality conditions for the convex program and matroid theory. We believe that the techniques introduced to show sparsity of optimal solutions to convex programs will be of independent interest. We also give a randomized algorithm that rounds a sparse fractional solution to a feasible integral solution to the original problem. To show the approximation guarantee, we utilize recent works on strongly log-concave polynomials and show new relationships between different convex programs studied for the problem. Finally, we use the estimation algorithm and sparsity results to give an efficient deterministic approximation algorithm with an approximation guarantee that depends solely on the dimension $d$.

Locally Private Hypothesis Selection

We initiate the study of hypothesis selection under local differential privacy. Given samples from an unknown probability distribution $p$ and a set of $k$ probability distributions $\mathcal{Q}$, we aim to output, under the constraints of $\varepsilon$-local differential privacy, a distribution from $\mathcal{Q}$ whose total variation distance to $p$ is comparable to the best such distribution. This is a generalization of the classic problem of $k$-wise simple hypothesis testing, which corresponds to when $p \in \mathcal{Q}$, and we wish to identify $p$. Absent privacy constraints, this problem requires $O(\log k)$ samples from $p$, and it was recently shown that the same complexity is achievable under (central) differential privacy. However, the naive approach to this problem under local differential privacy would require $\tilde O(k^2)$ samples. We first show that the constraint of local differential privacy incurs an exponential increase in cost: any algorithm for this problem requires at least $\Omega(k)$ samples. Second, for the special case of $k$-wise simple hypothesis testing, we provide a non-interactive algorithm which nearly matches this bound, requiring $\tilde O(k)$ samples. Finally, we provide sequentially interactive algorithms for the general case, requiring $\tilde O(k)$ samples and only $O(\log \log k)$ rounds of interactivity. Our algorithms are achieved through a reduction to maximum selection with adversarial comparators, a problem of independent interest for which we initiate study in the parallel setting. For this problem, we provide a family of algorithms for each number of allowed rounds of interaction $t$, as well as lower bounds showing that they are near-optimal for every $t$. Notably, our algorithms result in exponential improvements on the round complexity of previous methods.

The Power of Factorization Mechanisms in Local and Central Differential Privacy

We give new characterizations of the sample complexity of answering linear queries (statistical queries) in the local and central models of differential privacy: *In the non-interactive local model, we give the first approximate characterization of the sample complexity. Informally our bounds are tight to within polylogarithmic factors in the number of queries and desired accuracy. Our characterization extends to agnostic learning in the local model. *In the central model, we give a characterization of the sample complexity in the high-accuracy regime that is analogous to that of Nikolov, Talwar, and Zhang (STOC 2013), but is both quantitatively tighter and has a dramatically simpler proof. Our lower bounds apply equally to the empirical and population estimation problems. In both cases, our characterizations show that a particular factorization mechanism is approximately optimal, and the optimal sample complexity is bounded from above and below by well studied factorization norms of a matrix associated with the queries.

Proportional Volume Sampling and Approximation Algorithms for A-Optimal Design

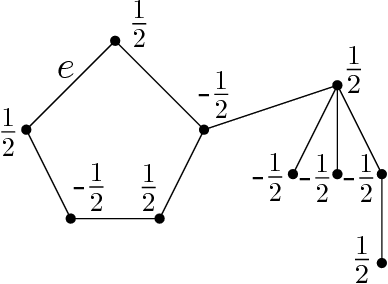
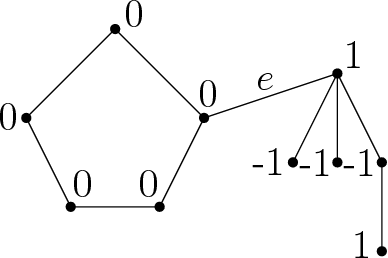
We study the optimal design problems where the goal is to choose a set of linear measurements to obtain the most accurate estimate of an unknown vector in $d$ dimensions. We study the $A$-optimal design variant where the objective is to minimize the average variance of the error in the maximum likelihood estimate of the vector being measured. The problem also finds applications in sensor placement in wireless networks, sparse least squares regression, feature selection for $k$-means clustering, and matrix approximation. In this paper, we introduce proportional volume sampling to obtain improved approximation algorithms for $A$-optimal design. Our main result is to obtain improved approximation algorithms for the $A$-optimal design problem by introducing the proportional volume sampling algorithm. Our results nearly optimal bounds in the asymptotic regime when the number of measurements done, $k$, is significantly more than the dimension $d$. We also give first approximation algorithms when $k$ is small including when $k=d$. The proportional volume-sampling algorithm also gives approximation algorithms for other optimal design objectives such as $D$-optimal design and generalized ratio objective matching or improving previous best known results. Interestingly, we show that a similar guarantee cannot be obtained for the $E$-optimal design problem. We also show that the $A$-optimal design problem is NP-hard to approximate within a fixed constant when $k=d$.

Approximate Near Neighbors for General Symmetric Norms

We show that every symmetric normed space admits an efficient nearest neighbor search data structure with doubly-logarithmic approximation. Specifically, for every $n$, $d = n^{o(1)}$, and every $d$-dimensional symmetric norm $\|\cdot\|$, there exists a data structure for $\mathrm{poly}(\log \log n)$-approximate nearest neighbor search over $\|\cdot\|$ for $n$-point datasets achieving $n^{o(1)}$ query time and $n^{1+o(1)}$ space. The main technical ingredient of the algorithm is a low-distortion embedding of a symmetric norm into a low-dimensional iterated product of top-$k$ norms. We also show that our techniques cannot be extended to general norms.