Differentially Private Multi-Sampling from Distributions

Many algorithms have been developed to estimate probability distributions subject to differential privacy (DP): such an algorithm takes as input independent samples from a distribution and estimates the density function in a way that is insensitive to any one sample. A recent line of work, initiated by Raskhodnikova et al. (Neurips '21), explores a weaker objective: a differentially private algorithm that approximates a single sample from the distribution. Raskhodnikova et al. studied the sample complexity of DP \emph{single-sampling} i.e., the minimum number of samples needed to perform this task. They showed that the sample complexity of DP single-sampling is less than the sample complexity of DP learning for certain distribution classes. We define two variants of \emph{multi-sampling}, where the goal is to privately approximate $m>1$ samples. This better models the realistic scenario where synthetic data is needed for exploratory data analysis. A baseline solution to \emph{multi-sampling} is to invoke a single-sampling algorithm $m$ times on independently drawn datasets of samples. When the data comes from a finite domain, we improve over the baseline by a factor of $m$ in the sample complexity. When the data comes from a Gaussian, Ghazi et al. (Neurips '23) show that \emph{single-sampling} can be performed under approximate differential privacy; we show it is possible to \emph{single- and multi-sample Gaussians with known covariance subject to pure DP}. Our solution uses a variant of the Laplace mechanism that is of independent interest. We also give sample complexity lower bounds, one for strong multi-sampling of finite distributions and another for weak multi-sampling of bounded-covariance Gaussians.

Confidential Federated Computations

Federated Learning and Analytics (FLA) have seen widespread adoption by technology platforms for processing sensitive on-device data. However, basic FLA systems have privacy limitations: they do not necessarily require anonymization mechanisms like differential privacy (DP), and provide limited protections against a potentially malicious service provider. Adding DP to a basic FLA system currently requires either adding excessive noise to each device's updates, or assuming an honest service provider that correctly implements the mechanism and only uses the privatized outputs. Secure multiparty computation (SMPC) -based oblivious aggregations can limit the service provider's access to individual user updates and improve DP tradeoffs, but the tradeoffs are still suboptimal, and they suffer from scalability challenges and susceptibility to Sybil attacks. This paper introduces a novel system architecture that leverages trusted execution environments (TEEs) and open-sourcing to both ensure confidentiality of server-side computations and provide externally verifiable privacy properties, bolstering the robustness and trustworthiness of private federated computations.

Shuffle Private Stochastic Convex Optimization

In shuffle privacy, each user sends a collection of randomized messages to a trusted shuffler, the shuffler randomly permutes these messages, and the resulting shuffled collection of messages must satisfy differential privacy. Prior work in this model has largely focused on protocols that use a single round of communication to compute algorithmic primitives like means, histograms, and counts. In this work, we present interactive shuffle protocols for stochastic convex optimization. Our optimization protocols rely on a new noninteractive protocol for summing vectors of bounded $\ell_2$ norm. By combining this sum subroutine with techniques including mini-batch stochastic gradient descent, accelerated gradient descent, and Nesterov's smoothing method, we obtain loss guarantees for a variety of convex loss functions that significantly improve on those of the local model and sometimes match those of the central model.

The Limits of Pan Privacy and Shuffle Privacy for Learning and Estimation

There has been a recent wave of interest in intermediate trust models for differential privacy that eliminate the need for a fully trusted central data collector, but overcome the limitations of local differential privacy. This interest has led to the introduction of the shuffle model (Cheu et al., EUROCRYPT 2019; Erlingsson et al., SODA 2019) and revisiting the pan-private model (Dwork et al., ITCS 2010). The message of this line of work is that, for a variety of low-dimensional problems---such as counts, means, and histograms---these intermediate models offer nearly as much power as central differential privacy. However, there has been considerably less success using these models for high-dimensional learning and estimation problems. In this work, we show that, for a variety of high-dimensional learning and estimation problems, both the shuffle model and the pan-private model inherently incur an exponential price in sample complexity relative to the central model. For example, we show that, private agnostic learning of parity functions over $d$ bits requires $\Omega(2^{d/2})$ samples in these models, and privately selecting the most common attribute from a set of $d$ choices requires $\Omega(d^{1/2})$ samples, both of which are exponential separations from the central model. Our work gives the first non-trivial lower bounds for these problems for both the pan-private model and the general multi-message shuffle model.

Connecting Robust Shuffle Privacy and Pan-Privacy

In the shuffle model of differential privacy, data-holding users send randomized messages to a secure shuffler, the shuffler permutes the messages, and the resulting collection of messages must be differentially private with regard to user data. In the pan-private model, an algorithm processes a stream of data while maintaining an internal state that is differentially private with regard to the stream data. We give evidence connecting these two apparently different models. Our results focus on robustly shuffle private protocols whose privacy guarantees are not greatly affected by malicious users. First, we give robustly shuffle private protocols and upper bounds for counting distinct elements and uniformity testing. Second, we use pan-private lower bounds to prove robustly shuffle private lower bounds for both problems. Focusing on the dependence on the domain size $k$, we find that both robust shuffle privacy and pan-privacy have additive accuracy $\Theta(\sqrt{k})$ for counting distinct elements and sample complexity $\tilde \Theta(k^{2/3})$ for uniformity testing. Both results polynomially separate central privacy and robust shuffle privacy. Finally, we show that this connection is useful in both directions: we give a pan-private adaptation of recent work on shuffle private histograms and use it to recover further separations between pan-privacy and interactive local privacy.

Private Query Release Assisted by Public Data

We study the problem of differentially private query release assisted by access to public data. In this problem, the goal is to answer a large class $\mathcal{H}$ of statistical queries with error no more than $\alpha$ using a combination of public and private samples. The algorithm is required to satisfy differential privacy only with respect to the private samples. We study the limits of this task in terms of the private and public sample complexities. First, we show that we can solve the problem for any query class $\mathcal{H}$ of finite VC-dimension using only $d/\alpha$ public samples and $\sqrt{p}d^{3/2}/\alpha^2$ private samples, where $d$ and $p$ are the VC-dimension and dual VC-dimension of $\mathcal{H}$, respectively. In comparison, with only private samples, this problem cannot be solved even for simple query classes with VC-dimension one, and without any private samples, a larger public sample of size $d/\alpha^2$ is needed. Next, we give sample complexity lower bounds that exhibit tight dependence on $p$ and $\alpha$. For the class of decision stumps, we give a lower bound of $\sqrt{p}/\alpha$ on the private sample complexity whenever the public sample size is less than $1/\alpha^2$. Given our upper bounds, this shows that the dependence on $\sqrt{p}$ is necessary in the private sample complexity. We also give a lower bound of $1/\alpha$ on the public sample complexity for a broad family of query classes, which by our upper bound, is tight in $\alpha$.

Skyline Identification in Multi-Armed Bandits

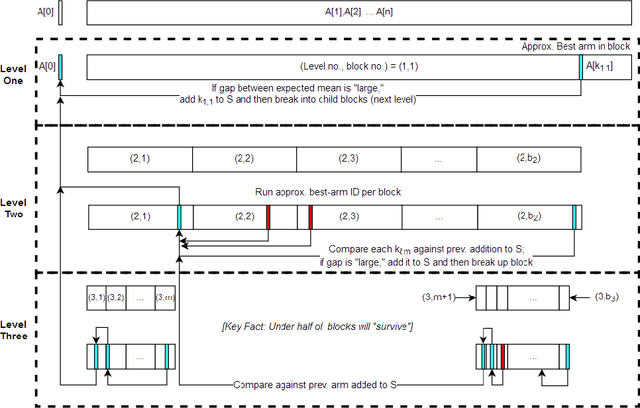
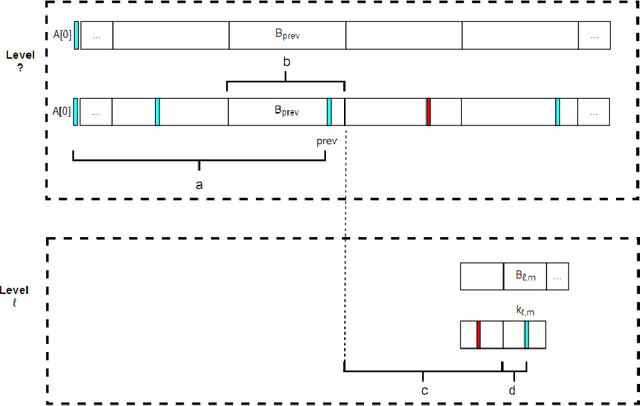
We introduce a variant of the classical PAC multi-armed bandit problem. There is an ordered set of $n$ arms $A[1],\dots,A[n]$, each with some stochastic reward drawn from some unknown bounded distribution. The goal is to identify the $skyline$ of the set $A$, consisting of all arms $A[i]$ such that $A[i]$ has larger expected reward than all lower-numbered arms $A[1],\dots,A[i-1]$. We define a natural notion of an $\varepsilon$-approximate skyline and prove matching upper and lower bounds for identifying an $\varepsilon$-skyline. Specifically, we show that in order to identify an $\varepsilon$-skyline from among $n$ arms with probability $1-\delta$, $$ \Theta\bigg(\frac{n}{\varepsilon^2} \cdot \min\bigg\{ \log\bigg(\frac{1}{\varepsilon \delta}\bigg), \log\bigg(\frac{n}{\delta}\bigg) \bigg\} \bigg) $$ samples are necessary and sufficient. When $\varepsilon \gg 1/n$, our results improve over the naive algorithm, which draws enough samples to approximate the expected reward of every arm; the algorithm of (Auer et al., AISTATS'16) for Pareto-optimal arm identification is likewise superseded. Our results show that the sample complexity of the skyline problem lies strictly in between that of best arm identification (Even-Dar et al., COLT'02) and that of approximating the expected reward of every arm.