Sample Complexity of Opinion Formation on Networks

Consider public health officials aiming to spread awareness about a new vaccine in a community interconnected by a social network. How can they distribute information with minimal resources, ensuring community-wide understanding that aligns with the actual facts? This concern mirrors numerous real-world situations. In this paper, we initialize the study of sample complexity in opinion formation to solve this problem. Our model is built on the recognized opinion formation game, where we regard each agent's opinion as a data-derived model parameter, not just a real number as in prior studies. Such an extension offers a wider understanding of opinion formation and ties closely with federated learning. Through this formulation, we characterize the sample complexity bounds for any network and also show asymptotically tight bounds for specific network structures. Intriguingly, we discover optimal strategies often allocate samples inversely to the degree, hinting at vital policy implications. Our findings are empirically validated on both synthesized and real-world networks.

PAC-Learning for Strategic Classification

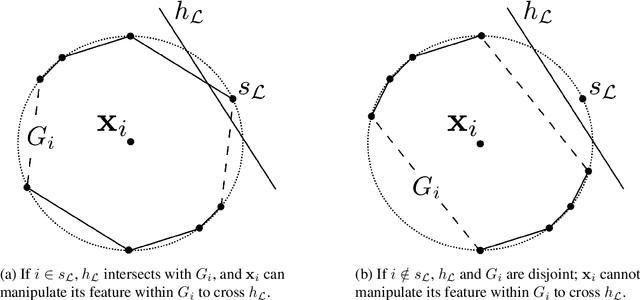
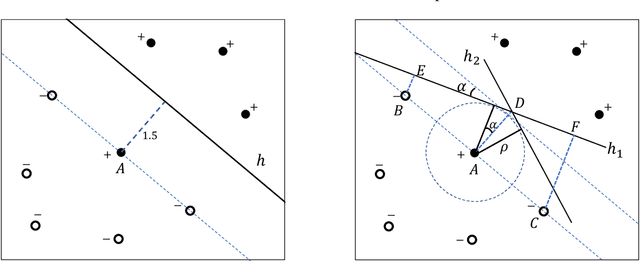
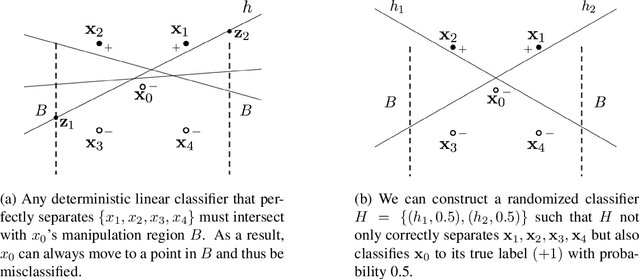
Machine learning (ML) algorithms may be susceptible to being gamed by individuals with knowledge of the algorithm (a.k.a. Goodhart's law). Such concerns have motivated a surge of recent work on strategic classification where each data point is a self-interested agent and may strategically manipulate his features to induce a more desirable classification outcome for himself. Previous works assume agents have homogeneous preferences and all equally prefer the positive label. This paper generalizes strategic classification to settings where different data points may have different preferences over the classification outcomes. Besides a richer model, this generalization allows us to include evasion attacks in adversarial ML also as a special case of our model where positive [resp. negative] data points prefer the negative [resp. positive] label, and thus for the first time allows strategic and adversarial learning to be studied under the same framework. We introduce the strategic VC-dimension (SVC), which captures the PAC-learnability of a hypothesis class in our general strategic setup. SVC generalizes the notion of adversarial VC-dimension (AVC) introduced recently by Cullina et al. arXiv:1806.01471. We then instantiate our framework for arguably the most basic hypothesis class, i.e., linear classifiers. We fully characterize the statistical learnability of linear classifiers by pinning down its SVC and the computational tractability by pinning down the complexity of the empirical risk minimization problem. Our bound of SVC for linear classifiers also strictly generalizes the AVC bound for linear classifiers in arXiv:1806.01471. Finally, we briefly study the power of randomization in our strategic classification setup. We show that randomization may strictly increase the accuracy in general, but will not help in the special case of adversarial classification under evasion attacks.

Attention improves concentration when learning node embeddings

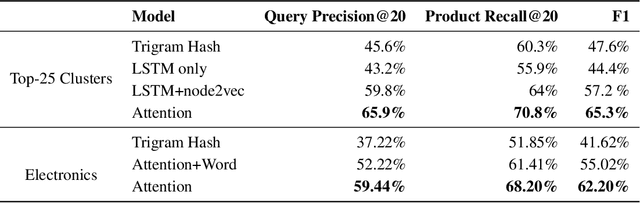
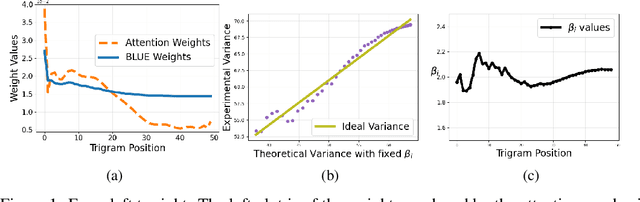
We consider the problem of predicting edges in a graph from node attributes in an e-commerce setting. Specifically, given nodes labelled with search query text, we want to predict links to related queries that share products. Experiments with a range of deep neural architectures show that simple feedforward networks with an attention mechanism perform best for learning embeddings. The simplicity of these models allows us to explain the performance of attention. We propose an analytically tractable model of query generation, AttEST, that views both products and the query text as vectors embedded in a latent space. We prove (and empirically validate) that the point-wise mutual information (PMI) matrix of the AttEST query text embeddings displays a low-rank behavior analogous to that observed in word embeddings. This low-rank property allows us to derive a loss function that maximizes the mutual information between related queries which is used to train an attention network to learn query embeddings. This AttEST network beats traditional memory-based LSTM architectures by over 20% on F-1 score. We justify this out-performance by showing that the weights from the attention mechanism correlate strongly with the weights of the best linear unbiased estimator (BLUE) for the product vectors, and conclude that attention plays an important role in variance reduction.

Skyline Identification in Multi-Armed Bandits

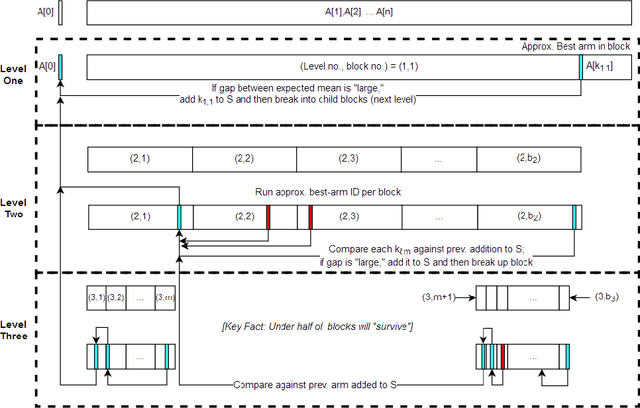
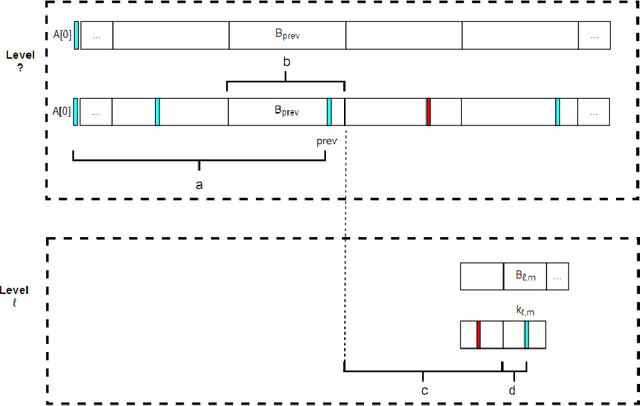
We introduce a variant of the classical PAC multi-armed bandit problem. There is an ordered set of $n$ arms $A[1],\dots,A[n]$, each with some stochastic reward drawn from some unknown bounded distribution. The goal is to identify the $skyline$ of the set $A$, consisting of all arms $A[i]$ such that $A[i]$ has larger expected reward than all lower-numbered arms $A[1],\dots,A[i-1]$. We define a natural notion of an $\varepsilon$-approximate skyline and prove matching upper and lower bounds for identifying an $\varepsilon$-skyline. Specifically, we show that in order to identify an $\varepsilon$-skyline from among $n$ arms with probability $1-\delta$, $$ \Theta\bigg(\frac{n}{\varepsilon^2} \cdot \min\bigg\{ \log\bigg(\frac{1}{\varepsilon \delta}\bigg), \log\bigg(\frac{n}{\delta}\bigg) \bigg\} \bigg) $$ samples are necessary and sufficient. When $\varepsilon \gg 1/n$, our results improve over the naive algorithm, which draws enough samples to approximate the expected reward of every arm; the algorithm of (Auer et al., AISTATS'16) for Pareto-optimal arm identification is likewise superseded. Our results show that the sample complexity of the skyline problem lies strictly in between that of best arm identification (Even-Dar et al., COLT'02) and that of approximating the expected reward of every arm.