Skyline Identification in Multi-Armed Bandits
Paper and Code
Jan 09, 2018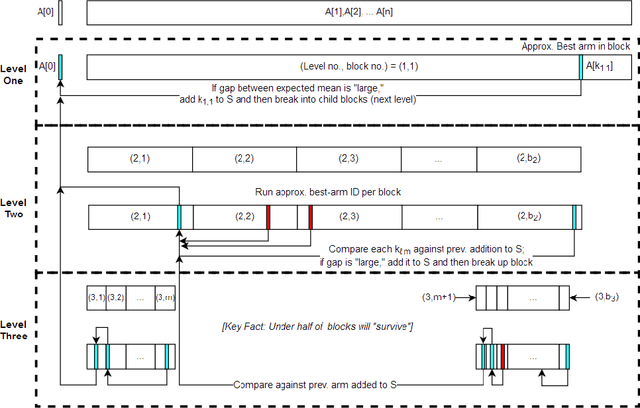
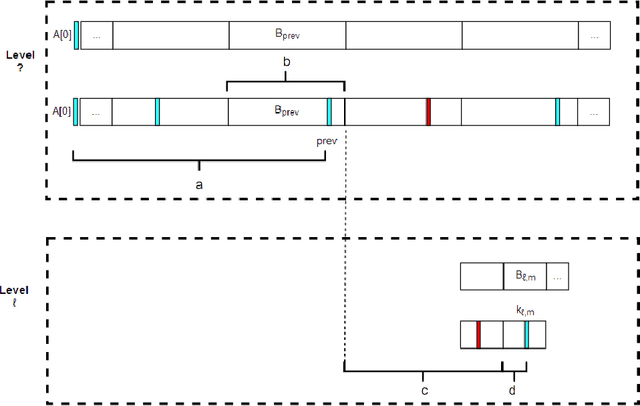
We introduce a variant of the classical PAC multi-armed bandit problem. There is an ordered set of $n$ arms $A[1],\dots,A[n]$, each with some stochastic reward drawn from some unknown bounded distribution. The goal is to identify the $skyline$ of the set $A$, consisting of all arms $A[i]$ such that $A[i]$ has larger expected reward than all lower-numbered arms $A[1],\dots,A[i-1]$. We define a natural notion of an $\varepsilon$-approximate skyline and prove matching upper and lower bounds for identifying an $\varepsilon$-skyline. Specifically, we show that in order to identify an $\varepsilon$-skyline from among $n$ arms with probability $1-\delta$, $$ \Theta\bigg(\frac{n}{\varepsilon^2} \cdot \min\bigg\{ \log\bigg(\frac{1}{\varepsilon \delta}\bigg), \log\bigg(\frac{n}{\delta}\bigg) \bigg\} \bigg) $$ samples are necessary and sufficient. When $\varepsilon \gg 1/n$, our results improve over the naive algorithm, which draws enough samples to approximate the expected reward of every arm; the algorithm of (Auer et al., AISTATS'16) for Pareto-optimal arm identification is likewise superseded. Our results show that the sample complexity of the skyline problem lies strictly in between that of best arm identification (Even-Dar et al., COLT'02) and that of approximating the expected reward of every arm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge