Benign Samples Matter! Fine-tuning On Outlier Benign Samples Severely Breaks Safety

Recent studies have uncovered a troubling vulnerability in the fine-tuning stage of large language models (LLMs): even fine-tuning on entirely benign datasets can lead to a significant increase in the harmfulness of LLM outputs. Building on this finding, our red teaming study takes this threat one step further by developing a more effective attack. Specifically, we analyze and identify samples within benign datasets that contribute most to safety degradation, then fine-tune LLMs exclusively on these samples. We approach this problem from an outlier detection perspective and propose Self-Inf-N, to detect and extract outliers for fine-tuning. Our findings reveal that fine-tuning LLMs on 100 outlier samples selected by Self-Inf-N in the benign datasets severely compromises LLM safety alignment. Extensive experiments across seven mainstream LLMs demonstrate that our attack exhibits high transferability across different architectures and remains effective in practical scenarios. Alarmingly, our results indicate that most existing mitigation strategies fail to defend against this attack, underscoring the urgent need for more robust alignment safeguards. Codes are available at https://github.com/GuanZihan/Benign-Samples-Matter.

Differentially Private Densest-$k$-Subgraph

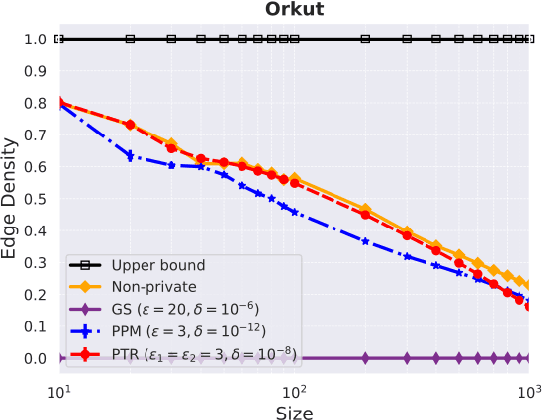
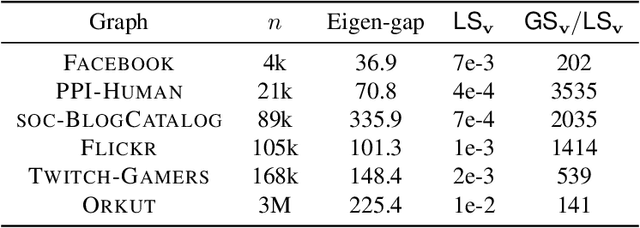
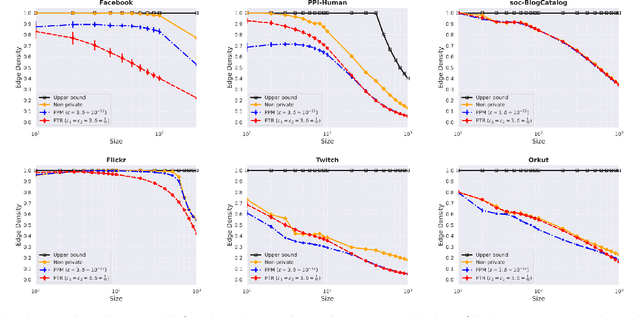
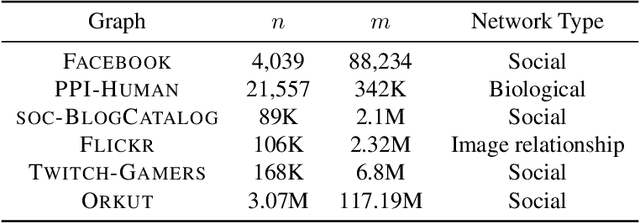
Many graph datasets involve sensitive network data, motivating the need for privacy-preserving graph mining. The Densest-$k$-subgraph (D$k$S) problem is a key primitive in graph mining that aims to extract a subset of $k$ vertices with the maximum internal connectivity. Although non-private algorithms are known for D$k$S, this paper is the first to design algorithms that offer formal differential privacy (DP) guarantees for the problem. We base our general approach on using the principal component (PC) of the graph adjacency matrix to output a subset of $k$ vertices under edge DP. For this task, we first consider output perturbation, which traditionally offer good scalability, but at the expense of utility. Our tight on the local sensitivity indicate a big gap with the global sensitivity, motivating the use of instance specific sensitive methods for private PC. Next, we derive a tight bound on the smooth sensitivity and show that it can be close to the global sensitivity. This leads us to consider the Propose-Test-Release (PTR) framework for private PC. Although computationally expensive in general, we design a novel approach for implementing PTR in the same time as computation of a non-private PC, while offering good utility for \DkS{}. Additionally, we also consider the iterative private power method (PPM) for private PC, albeit it is significantly slower than PTR on large networks. We run our methods on diverse real-world networks, with the largest having 3 million vertices, and show good privacy-utility trade-offs. Although PTR requires a slightly larger privacy budget, on average, it achieves a 180-fold improvement in runtime over PPM.

Contrastive explainable clustering with differential privacy

This paper presents a novel approach in Explainable AI (XAI), integrating contrastive explanations with differential privacy in clustering methods. For several basic clustering problems, including $k$-median and $k$-means, we give efficient differential private contrastive explanations that achieve essentially the same explanations as those that non-private clustering explanations can obtain. We define contrastive explanations as the utility difference between the original clustering utility and utility from clustering with a specifically fixed centroid. In each contrastive scenario, we designate a specific data point as the fixed centroid position, enabling us to measure the impact of this constraint on clustering utility under differential privacy. Extensive experiments across various datasets show our method's effectiveness in providing meaningful explanations without significantly compromising data privacy or clustering utility. This underscores our contribution to privacy-aware machine learning, demonstrating the feasibility of achieving a balance between privacy and utility in the explanation of clustering tasks.

Differentially private exact recovery for stochastic block models

Stochastic block models (SBMs) are a very commonly studied network model for community detection algorithms. In the standard form of an SBM, the $n$ vertices (or nodes) of a graph are generally divided into multiple pre-determined communities (or clusters). Connections between pairs of vertices are generated randomly and independently with pre-defined probabilities, which depend on the communities containing the two nodes. A fundamental problem in SBMs is the recovery of the community structure, and sharp information-theoretic bounds are known for recoverability for many versions of SBMs. Our focus here is the recoverability problem in SBMs when the network is private. Under the edge differential privacy model, we derive conditions for exact recoverability in three different versions of SBMs, namely Asymmetric SBM (when communities have non-uniform sizes), General Structure SBM (with outliers), and Censored SBM (with edge features). Our private algorithms have polynomial running time w.r.t. the input graph's size, and match the recovery thresholds of the non-private setting when $\epsilon\rightarrow\infty$. In contrast, the previous best results for recoverability in SBMs only hold for the symmetric case (equal size communities), and run in quasi-polynomial time, or in polynomial time with recovery thresholds being tight up to some constants from the non-private settings.

Efficient PAC Learnability of Dynamical Systems Over Multilayer Networks

Networked dynamical systems are widely used as formal models of real-world cascading phenomena, such as the spread of diseases and information. Prior research has addressed the problem of learning the behavior of an unknown dynamical system when the underlying network has a single layer. In this work, we study the learnability of dynamical systems over multilayer networks, which are more realistic and challenging. First, we present an efficient PAC learning algorithm with provable guarantees to show that the learner only requires a small number of training examples to infer an unknown system. We further provide a tight analysis of the Natarajan dimension which measures the model complexity. Asymptotically, our bound on the Nararajan dimension is tight for almost all multilayer graphs. The techniques and insights from our work provide the theoretical foundations for future investigations of learning problems for multilayer dynamical systems.

UFID: A Unified Framework for Input-level Backdoor Detection on Diffusion Models

Diffusion Models are vulnerable to backdoor attacks, where malicious attackers inject backdoors by poisoning some parts of the training samples during the training stage. This poses a serious threat to the downstream users, who query the diffusion models through the API or directly download them from the internet. To mitigate the threat of backdoor attacks, there have been a plethora of investigations on backdoor detections. However, none of them designed a specialized backdoor detection method for diffusion models, rendering the area much under-explored. Moreover, these prior methods mainly focus on the traditional neural networks in the classification task, which cannot be adapted to the backdoor detections on the generative task easily. Additionally, most of the prior methods require white-box access to model weights and architectures, or the probability logits as additional information, which are not always practical. In this paper, we propose a Unified Framework for Input-level backdoor Detection (UFID) on the diffusion models, which is motivated by observations in the diffusion models and further validated with a theoretical causality analysis. Extensive experiments across different datasets on both conditional and unconditional diffusion models show that our method achieves a superb performance on detection effectiveness and run-time efficiency. The code is available at https://github.com/GuanZihan/official_UFID.

Learning the Topology and Behavior of Discrete Dynamical Systems

Discrete dynamical systems are commonly used to model the spread of contagions on real-world networks. Under the PAC framework, existing research has studied the problem of learning the behavior of a system, assuming that the underlying network is known. In this work, we focus on a more challenging setting: to learn both the behavior and the underlying topology of a black-box system. We show that, in general, this learning problem is computationally intractable. On the positive side, we present efficient learning methods under the PAC model when the underlying graph of the dynamical system belongs to some classes. Further, we examine a relaxed setting where the topology of an unknown system is partially observed. For this case, we develop an efficient PAC learner to infer the system and establish the sample complexity. Lastly, we present a formal analysis of the expressive power of the hypothesis class of dynamical systems where both the topology and behavior are unknown, using the well-known formalism of the Natarajan dimension. Our results provide a theoretical foundation for learning both the behavior and topology of discrete dynamical systems.

Sample Complexity of Opinion Formation on Networks

Consider public health officials aiming to spread awareness about a new vaccine in a community interconnected by a social network. How can they distribute information with minimal resources, ensuring community-wide understanding that aligns with the actual facts? This concern mirrors numerous real-world situations. In this paper, we initialize the study of sample complexity in opinion formation to solve this problem. Our model is built on the recognized opinion formation game, where we regard each agent's opinion as a data-derived model parameter, not just a real number as in prior studies. Such an extension offers a wider understanding of opinion formation and ties closely with federated learning. Through this formulation, we characterize the sample complexity bounds for any network and also show asymptotically tight bounds for specific network structures. Intriguingly, we discover optimal strategies often allocate samples inversely to the degree, hinting at vital policy implications. Our findings are empirically validated on both synthesized and real-world networks.

A Look into Causal Effects under Entangled Treatment in Graphs: Investigating the Impact of Contact on MRSA Infection

Methicillin-resistant Staphylococcus aureus (MRSA) is a type of bacteria resistant to certain antibiotics, making it difficult to prevent MRSA infections. Among decades of efforts to conquer infectious diseases caused by MRSA, many studies have been proposed to estimate the causal effects of close contact (treatment) on MRSA infection (outcome) from observational data. In this problem, the treatment assignment mechanism plays a key role as it determines the patterns of missing counterfactuals -- the fundamental challenge of causal effect estimation. Most existing observational studies for causal effect learning assume that the treatment is assigned individually for each unit. However, on many occasions, the treatments are pairwisely assigned for units that are connected in graphs, i.e., the treatments of different units are entangled. Neglecting the entangled treatments can impede the causal effect estimation. In this paper, we study the problem of causal effect estimation with treatment entangled in a graph. Despite a few explorations for entangled treatments, this problem still remains challenging due to the following challenges: (1) the entanglement brings difficulties in modeling and leveraging the unknown treatment assignment mechanism; (2) there may exist hidden confounders which lead to confounding biases in causal effect estimation; (3) the observational data is often time-varying. To tackle these challenges, we propose a novel method NEAT, which explicitly leverages the graph structure to model the treatment assignment mechanism, and mitigates confounding biases based on the treatment assignment modeling. We also extend our method into a dynamic setting to handle time-varying observational data. Experiments on both synthetic datasets and a real-world MRSA dataset validate the effectiveness of the proposed method, and provide insights for future applications.

Spatial-Temporal Networks for Antibiogram Pattern Prediction

An antibiogram is a periodic summary of antibiotic resistance results of organisms from infected patients to selected antimicrobial drugs. Antibiograms help clinicians to understand regional resistance rates and select appropriate antibiotics in prescriptions. In practice, significant combinations of antibiotic resistance may appear in different antibiograms, forming antibiogram patterns. Such patterns may imply the prevalence of some infectious diseases in certain regions. Thus it is of crucial importance to monitor antibiotic resistance trends and track the spread of multi-drug resistant organisms. In this paper, we propose a novel problem of antibiogram pattern prediction that aims to predict which patterns will appear in the future. Despite its importance, tackling this problem encounters a series of challenges and has not yet been explored in the literature. First of all, antibiogram patterns are not i.i.d as they may have strong relations with each other due to genomic similarities of the underlying organisms. Second, antibiogram patterns are often temporally dependent on the ones that are previously detected. Furthermore, the spread of antibiotic resistance can be significantly influenced by nearby or similar regions. To address the above challenges, we propose a novel Spatial-Temporal Antibiogram Pattern Prediction framework, STAPP, that can effectively leverage the pattern correlations and exploit the temporal and spatial information. We conduct extensive experiments on a real-world dataset with antibiogram reports of patients from 1999 to 2012 for 203 cities in the United States. The experimental results show the superiority of STAPP against several competitive baselines.