Efficient PAC Learnability of Dynamical Systems Over Multilayer Networks

Networked dynamical systems are widely used as formal models of real-world cascading phenomena, such as the spread of diseases and information. Prior research has addressed the problem of learning the behavior of an unknown dynamical system when the underlying network has a single layer. In this work, we study the learnability of dynamical systems over multilayer networks, which are more realistic and challenging. First, we present an efficient PAC learning algorithm with provable guarantees to show that the learner only requires a small number of training examples to infer an unknown system. We further provide a tight analysis of the Natarajan dimension which measures the model complexity. Asymptotically, our bound on the Nararajan dimension is tight for almost all multilayer graphs. The techniques and insights from our work provide the theoretical foundations for future investigations of learning problems for multilayer dynamical systems.

Learning the Topology and Behavior of Discrete Dynamical Systems

Discrete dynamical systems are commonly used to model the spread of contagions on real-world networks. Under the PAC framework, existing research has studied the problem of learning the behavior of a system, assuming that the underlying network is known. In this work, we focus on a more challenging setting: to learn both the behavior and the underlying topology of a black-box system. We show that, in general, this learning problem is computationally intractable. On the positive side, we present efficient learning methods under the PAC model when the underlying graph of the dynamical system belongs to some classes. Further, we examine a relaxed setting where the topology of an unknown system is partially observed. For this case, we develop an efficient PAC learner to infer the system and establish the sample complexity. Lastly, we present a formal analysis of the expressive power of the hypothesis class of dynamical systems where both the topology and behavior are unknown, using the well-known formalism of the Natarajan dimension. Our results provide a theoretical foundation for learning both the behavior and topology of discrete dynamical systems.

Finding Nontrivial Minimum Fixed Points in Discrete Dynamical Systems

Networked discrete dynamical systems are often used to model the spread of contagions and decision-making by agents in coordination games. Fixed points of such dynamical systems represent configurations to which the system converges. In the dissemination of undesirable contagions (such as rumors and misinformation), convergence to fixed points with a small number of affected nodes is a desirable goal. Motivated by such considerations, we formulate a novel optimization problem of finding a nontrivial fixed point of the system with the minimum number of affected nodes. We establish that, unless P = NP, there is no polynomial time algorithm for approximating a solution to this problem to within the factor n^1-\epsilon for any constant epsilon > 0. To cope with this computational intractability, we identify several special cases for which the problem can be solved efficiently. Further, we introduce an integer linear program to address the problem for networks of reasonable sizes. For solving the problem on larger networks, we propose a general heuristic framework along with greedy selection methods. Extensive experimental results on real-world networks demonstrate the effectiveness of the proposed heuristics.

Guided Deep List: Automating the Generation of Epidemiological Line Lists from Open Sources

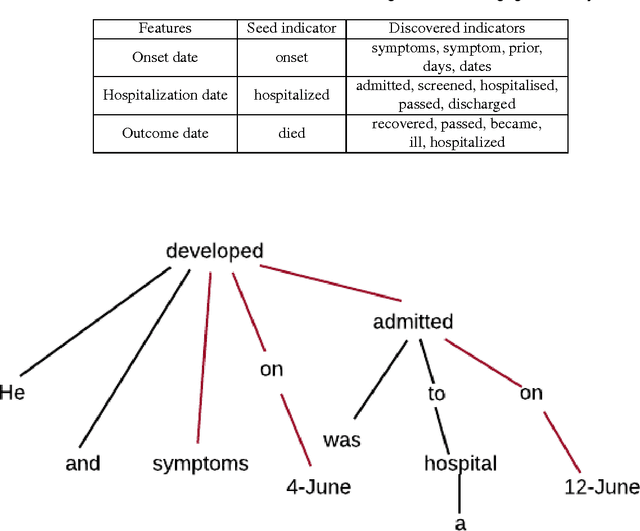
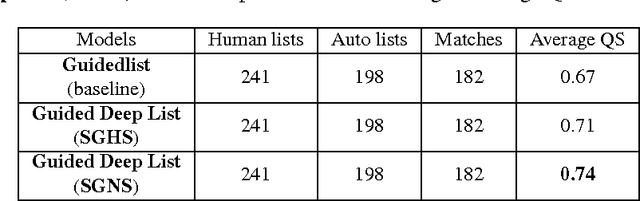
Real-time monitoring and responses to emerging public health threats rely on the availability of timely surveillance data. During the early stages of an epidemic, the ready availability of line lists with detailed tabular information about laboratory-confirmed cases can assist epidemiologists in making reliable inferences and forecasts. Such inferences are crucial to understand the epidemiology of a specific disease early enough to stop or control the outbreak. However, construction of such line lists requires considerable human supervision and therefore, difficult to generate in real-time. In this paper, we motivate Guided Deep List, the first tool for building automated line lists (in near real-time) from open source reports of emerging disease outbreaks. Specifically, we focus on deriving epidemiological characteristics of an emerging disease and the affected population from reports of illness. Guided Deep List uses distributed vector representations (ala word2vec) to discover a set of indicators for each line list feature. This discovery of indicators is followed by the use of dependency parsing based techniques for final extraction in tabular form. We evaluate the performance of Guided Deep List against a human annotated line list provided by HealthMap corresponding to MERS outbreaks in Saudi Arabia. We demonstrate that Guided Deep List extracts line list features with increased accuracy compared to a baseline method. We further show how these automatically extracted line list features can be used for making epidemiological inferences, such as inferring demographics and symptoms-to-hospitalization period of affected individuals.