IGraSS: Learning to Identify Infrastructure Networks from Satellite Imagery by Iterative Graph-constrained Semantic Segmentation

Accurate canal network mapping is essential for water management, including irrigation planning and infrastructure maintenance. State-of-the-art semantic segmentation models for infrastructure mapping, such as roads, rely on large, well-annotated remote sensing datasets. However, incomplete or inadequate ground truth can hinder these learning approaches. Many infrastructure networks have graph-level properties such as reachability to a source (like canals) or connectivity (roads) that can be leveraged to improve these existing ground truth. This paper develops a novel iterative framework IGraSS, combining a semantic segmentation module-incorporating RGB and additional modalities (NDWI, DEM)-with a graph-based ground-truth refinement module. The segmentation module processes satellite imagery patches, while the refinement module operates on the entire data viewing the infrastructure network as a graph. Experiments show that IGraSS reduces unreachable canal segments from around 18% to 3%, and training with refined ground truth significantly improves canal identification. IGraSS serves as a robust framework for both refining noisy ground truth and mapping canal networks from remote sensing imagery. We also demonstrate the effectiveness and generalizability of IGraSS using road networks as an example, applying a different graph-theoretic constraint to complete road networks.

Knowledge-Informed Deep Learning for Irrigation Type Mapping from Remote Sensing

Accurate mapping of irrigation methods is crucial for sustainable agricultural practices and food systems. However, existing models that rely solely on spectral features from satellite imagery are ineffective due to the complexity of agricultural landscapes and limited training data, making this a challenging problem. We present Knowledge-Informed Irrigation Mapping (KIIM), a novel Swin-Transformer based approach that uses (i) a specialized projection matrix to encode crop to irrigation probability, (ii) a spatial attention map to identify agricultural lands from non-agricultural lands, (iii) bi-directional cross-attention to focus complementary information from different modalities, and (iv) a weighted ensemble for combining predictions from images and crop information. Our experimentation on five states in the US shows up to 22.9\% (IoU) improvement over baseline with a 71.4% (IoU) improvement for hard-to-classify drip irrigation. In addition, we propose a two-phase transfer learning approach to enhance cross-state irrigation mapping, achieving a 51% IoU boost in a state with limited labeled data. The ability to achieve baseline performance with only 40% of the training data highlights its efficiency, reducing the dependency on extensive manual labeling efforts and making large-scale, automated irrigation mapping more feasible and cost-effective.

IrrMap: A Large-Scale Comprehensive Dataset for Irrigation Method Mapping

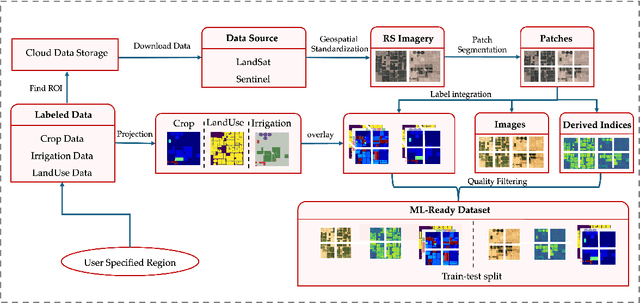
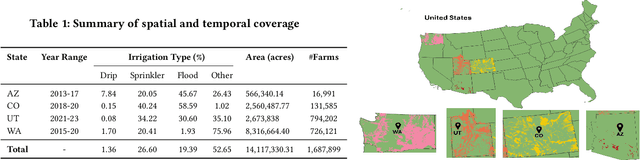
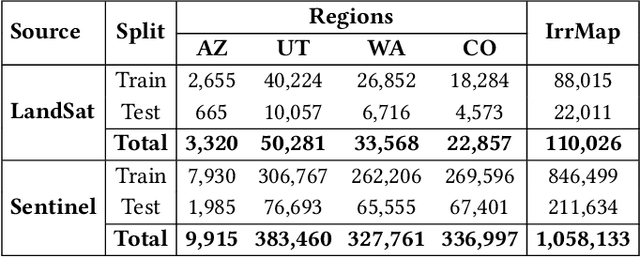
We introduce IrrMap, the first large-scale dataset (1.1 million patches) for irrigation method mapping across regions. IrrMap consists of multi-resolution satellite imagery from LandSat and Sentinel, along with key auxiliary data such as crop type, land use, and vegetation indices. The dataset spans 1,687,899 farms and 14,117,330 acres across multiple western U.S. states from 2013 to 2023, providing a rich and diverse foundation for irrigation analysis and ensuring geospatial alignment and quality control. The dataset is ML-ready, with standardized 224x224 GeoTIFF patches, the multiple input modalities, carefully chosen train-test-split data, and accompanying dataloaders for seamless deep learning model training andbenchmarking in irrigation mapping. The dataset is also accompanied by a complete pipeline for dataset generation, enabling researchers to extend IrrMap to new regions for irrigation data collection or adapt it with minimal effort for other similar applications in agricultural and geospatial analysis. We also analyze the irrigation method distribution across crop groups, spatial irrigation patterns (using Shannon diversity indices), and irrigated area variations for both LandSat and Sentinel, providing insights into regional and resolution-based differences. To promote further exploration, we openly release IrrMap, along with the derived datasets, benchmark models, and pipeline code, through a GitHub repository: https://github.com/Nibir088/IrrMap and Data repository: https://huggingface.co/Nibir/IrrMap, providing comprehensive documentation and implementation details.

A Unifying Information-theoretic Perspective on Evaluating Generative Models

Considering the difficulty of interpreting generative model output, there is significant current research focused on determining meaningful evaluation metrics. Several recent approaches utilize "precision" and "recall," borrowed from the classification domain, to individually quantify the output fidelity (realism) and output diversity (representation of the real data variation), respectively. With the increase in metric proposals, there is a need for a unifying perspective, allowing for easier comparison and clearer explanation of their benefits and drawbacks. To this end, we unify a class of kth-nearest-neighbors (kNN)-based metrics under an information-theoretic lens using approaches from kNN density estimation. Additionally, we propose a tri-dimensional metric composed of Precision Cross-Entropy (PCE), Recall Cross-Entropy (RCE), and Recall Entropy (RE), which separately measure fidelity and two distinct aspects of diversity, inter- and intra-class. Our domain-agnostic metric, derived from the information-theoretic concepts of entropy and cross-entropy, can be dissected for both sample- and mode-level analysis. Our detailed experimental results demonstrate the sensitivity of our metric components to their respective qualities and reveal undesirable behaviors of other metrics.

IrrNet: Advancing Irrigation Mapping with Incremental Patch Size Training on Remote Sensing Imagery

Irrigation mapping plays a crucial role in effective water management, essential for preserving both water quality and quantity, and is key to mitigating the global issue of water scarcity. The complexity of agricultural fields, adorned with diverse irrigation practices, especially when multiple systems coexist in close quarters, poses a unique challenge. This complexity is further compounded by the nature of Landsat's remote sensing data, where each pixel is rich with densely packed information, complicating the task of accurate irrigation mapping. In this study, we introduce an innovative approach that employs a progressive training method, which strategically increases patch sizes throughout the training process, utilizing datasets from Landsat 5 and 7, labeled with the WRLU dataset for precise labeling. This initial focus allows the model to capture detailed features, progressively shifting to broader, more general features as the patch size enlarges. Remarkably, our method enhances the performance of existing state-of-the-art models by approximately 20%. Furthermore, our analysis delves into the significance of incorporating various spectral bands into the model, assessing their impact on performance. The findings reveal that additional bands are instrumental in enabling the model to discern finer details more effectively. This work sets a new standard for leveraging remote sensing imagery in irrigation mapping.

High-resolution synthetic residential energy use profiles for the United States

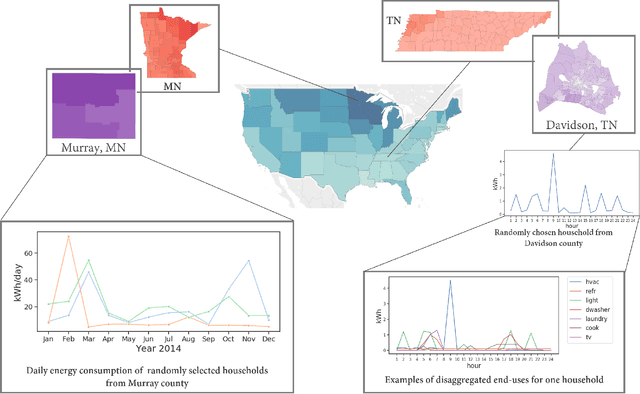
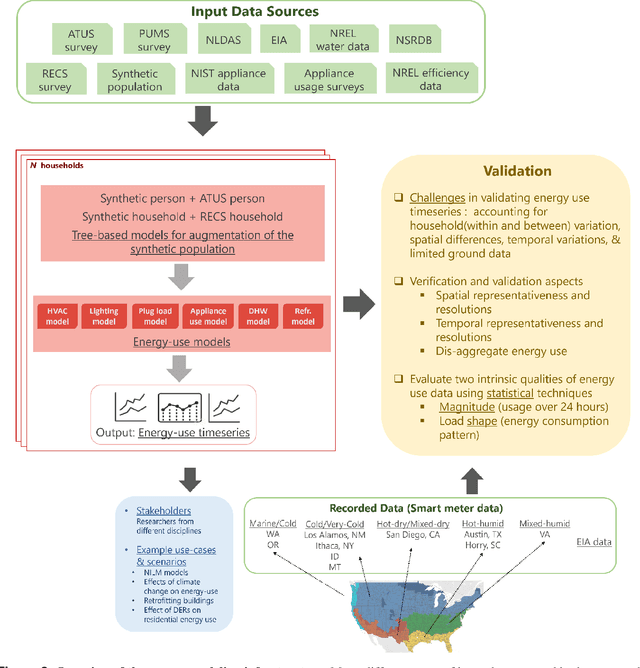
Efficient energy consumption is crucial for achieving sustainable energy goals in the era of climate change and grid modernization. Thus, it is vital to understand how energy is consumed at finer resolutions such as household in order to plan demand-response events or analyze the impacts of weather, electricity prices, electric vehicles, solar, and occupancy schedules on energy consumption. However, availability and access to detailed energy-use data, which would enable detailed studies, has been rare. In this paper, we release a unique, large-scale, synthetic, residential energy-use dataset for the residential sector across the contiguous United States covering millions of households. The data comprise of hourly energy use profiles for synthetic households, disaggregated into Thermostatically Controlled Loads (TCL) and appliance use. The underlying framework is constructed using a bottom-up approach. Diverse open-source surveys and first principles models are used for end-use modeling. Extensive validation of the synthetic dataset has been conducted through comparisons with reported energy-use data. We present a detailed, open, high-resolution, residential energy-use dataset for the United States.

A Scalable Data-Driven Technique for Joint Evacuation Routing and Scheduling Problems

Evacuation planning is a crucial part of disaster management where the goal is to relocate people to safety and minimize casualties. Every evacuation plan has two essential components: routing and scheduling. However, joint optimization of these two components with objectives such as minimizing average evacuation time or evacuation completion time, is a computationally hard problem. To approach it, we present MIP-LNS, a scalable optimization method that combines heuristic search with mathematical optimization and can optimize a variety of objective functions. We use real-world road network and population data from Harris County in Houston, Texas, and apply MIP-LNS to find evacuation routes and schedule for the area. We show that, within a given time limit, our proposed method finds better solutions than existing methods in terms of average evacuation time, evacuation completion time and optimality guarantee of the solutions. We perform agent-based simulations of evacuation in our study area to demonstrate the efficacy and robustness of our solution. We show that our prescribed evacuation plan remains effective even if the evacuees deviate from the suggested schedule upto a certain extent. We also examine how evacuation plans are affected by road failures. Our results show that MIP-LNS can use information regarding estimated deadline of roads to come up with better evacuation plans in terms evacuating more people successfully and conveniently.

Stratified Graph Spectra

In classic graph signal processing, given a real-valued graph signal, its graph Fourier transform is typically defined as the series of inner products between the signal and each eigenvector of the graph Laplacian. Unfortunately, this definition is not mathematically valid in the cases of vector-valued graph signals which however are typical operands in the state-of-the-art graph learning modeling and analyses. Seeking a generalized transformation decoding the magnitudes of eigencomponents from vector-valued signals is thus the main objective of this paper. Several attempts are explored, and also it is found that performing the transformation at hierarchical levels of adjacency help profile the spectral characteristics of signals more insightfully. The proposed methods are introduced as a new tool assisting on diagnosing and profiling behaviors of graph learning models.