Efficient PAC Learnability of Dynamical Systems Over Multilayer Networks

Networked dynamical systems are widely used as formal models of real-world cascading phenomena, such as the spread of diseases and information. Prior research has addressed the problem of learning the behavior of an unknown dynamical system when the underlying network has a single layer. In this work, we study the learnability of dynamical systems over multilayer networks, which are more realistic and challenging. First, we present an efficient PAC learning algorithm with provable guarantees to show that the learner only requires a small number of training examples to infer an unknown system. We further provide a tight analysis of the Natarajan dimension which measures the model complexity. Asymptotically, our bound on the Nararajan dimension is tight for almost all multilayer graphs. The techniques and insights from our work provide the theoretical foundations for future investigations of learning problems for multilayer dynamical systems.

Learning the Topology and Behavior of Discrete Dynamical Systems

Discrete dynamical systems are commonly used to model the spread of contagions on real-world networks. Under the PAC framework, existing research has studied the problem of learning the behavior of a system, assuming that the underlying network is known. In this work, we focus on a more challenging setting: to learn both the behavior and the underlying topology of a black-box system. We show that, in general, this learning problem is computationally intractable. On the positive side, we present efficient learning methods under the PAC model when the underlying graph of the dynamical system belongs to some classes. Further, we examine a relaxed setting where the topology of an unknown system is partially observed. For this case, we develop an efficient PAC learner to infer the system and establish the sample complexity. Lastly, we present a formal analysis of the expressive power of the hypothesis class of dynamical systems where both the topology and behavior are unknown, using the well-known formalism of the Natarajan dimension. Our results provide a theoretical foundation for learning both the behavior and topology of discrete dynamical systems.

Finding Nontrivial Minimum Fixed Points in Discrete Dynamical Systems

Networked discrete dynamical systems are often used to model the spread of contagions and decision-making by agents in coordination games. Fixed points of such dynamical systems represent configurations to which the system converges. In the dissemination of undesirable contagions (such as rumors and misinformation), convergence to fixed points with a small number of affected nodes is a desirable goal. Motivated by such considerations, we formulate a novel optimization problem of finding a nontrivial fixed point of the system with the minimum number of affected nodes. We establish that, unless P = NP, there is no polynomial time algorithm for approximating a solution to this problem to within the factor n^1-\epsilon for any constant epsilon > 0. To cope with this computational intractability, we identify several special cases for which the problem can be solved efficiently. Further, we introduce an integer linear program to address the problem for networks of reasonable sizes. For solving the problem on larger networks, we propose a general heuristic framework along with greedy selection methods. Extensive experimental results on real-world networks demonstrate the effectiveness of the proposed heuristics.

Resource Sharing Through Multi-Round Matchings

Applications such as employees sharing office spaces over a workweek can be modeled as problems where agents are matched to resources over multiple rounds. Agents' requirements limit the set of compatible resources and the rounds in which they want to be matched. Viewing such an application as a multi-round matching problem on a bipartite compatibility graph between agents and resources, we show that a solution (i.e., a set of matchings, with one matching per round) can be found efficiently if one exists. To cope with situations where a solution does not exist, we consider two extensions. In the first extension, a benefit function is defined for each agent and the objective is to find a multi-round matching to maximize the total benefit. For a general class of benefit functions satisfying certain properties (including diminishing returns), we show that this multi-round matching problem is efficiently solvable. This class includes utilitarian and Rawlsian welfare functions. For another benefit function, we show that the maximization problem is NP-hard. In the second extension, the objective is to generate advice to each agent (i.e., a subset of requirements to be relaxed) subject to a budget constraint so that the agent can be matched. We show that this budget-constrained advice generation problem is NP-hard. For this problem, we develop an integer linear programming formulation as well as a heuristic based on local search. We experimentally evaluate our algorithms on synthetic networks and apply them to two real-world situations: shared office spaces and matching courses to classrooms.

Towards Auditing Unsupervised Learning Algorithms and Human Processes For Fairness

Existing work on fairness typically focuses on making known machine learning algorithms fairer. Fair variants of classification, clustering, outlier detection and other styles of algorithms exist. However, an understudied area is the topic of auditing an algorithm's output to determine fairness. Existing work has explored the two group classification problem for binary protected status variables using standard definitions of statistical parity. Here we build upon the area of auditing by exploring the multi-group setting under more complex definitions of fairness.

Explainable Clustering via Exemplars: Complexity and Efficient Approximation Algorithms

Explainable AI (XAI) is an important developing area but remains relatively understudied for clustering. We propose an explainable-by-design clustering approach that not only finds clusters but also exemplars to explain each cluster. The use of exemplars for understanding is supported by the exemplar-based school of concept definition in psychology. We show that finding a small set of exemplars to explain even a single cluster is computationally intractable; hence, the overall problem is challenging. We develop an approximation algorithm that provides provable performance guarantees with respect to clustering quality as well as the number of exemplars used. This basic algorithm explains all the instances in every cluster whilst another approximation algorithm uses a bounded number of exemplars to allow simpler explanations and provably covers a large fraction of all the instances. Experimental results show that our work is useful in domains involving difficult to understand deep embeddings of images and text.

Resource Allocation to Agents with Restrictions: Maximizing Likelihood with Minimum Compromise

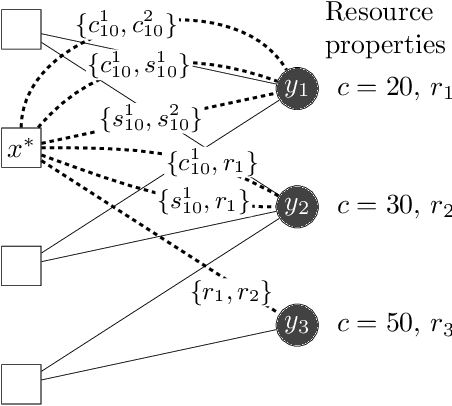
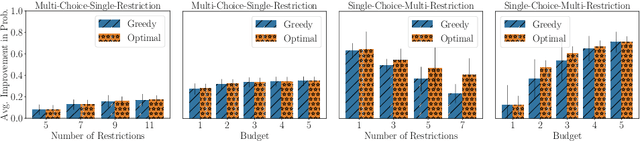
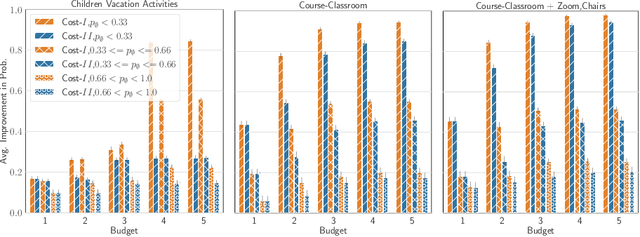
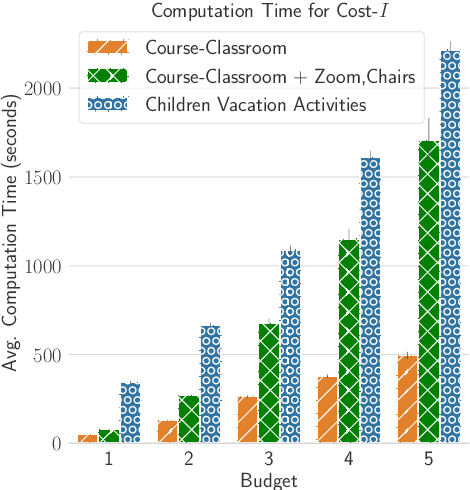
Many scenarios where agents with restrictions compete for resources can be cast as maximum matching problems on bipartite graphs. Our focus is on resource allocation problems where agents may have restrictions that make them incompatible with some resources. We assume that a Principle chooses a maximum matching randomly so that each agent is matched to a resource with some probability. Agents would like to improve their chances of being matched by modifying their restrictions within certain limits. The Principle's goal is to advise an unsatisfied agent to relax its restrictions so that the total cost of relaxation is within a budget (chosen by the agent) and the increase in the probability of being assigned a resource is maximized. We establish hardness results for some variants of this budget-constrained maximization problem and present algorithmic results for other variants. We experimentally evaluate our methods on synthetic datasets as well as on two novel real-world datasets: a vacation activities dataset and a classrooms dataset.

Efficient Algorithms for Generating Provably Near-Optimal Cluster Descriptors for Explainability

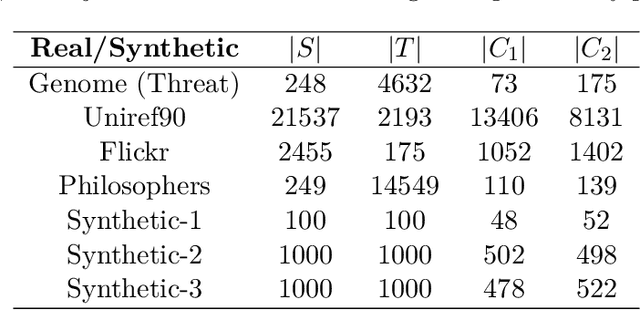
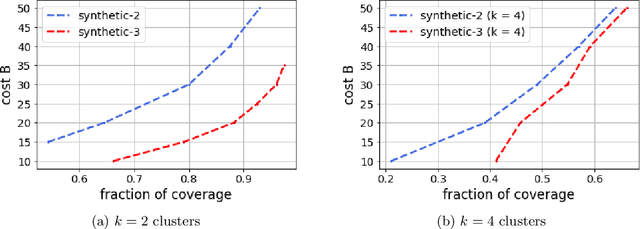
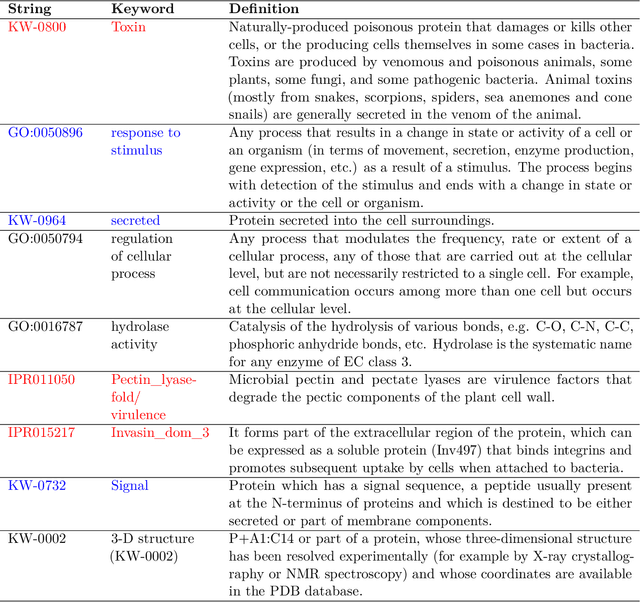
Improving the explainability of the results from machine learning methods has become an important research goal. Here, we study the problem of making clusters more interpretable by extending a recent approach of [Davidson et al., NeurIPS 2018] for constructing succinct representations for clusters. Given a set of objects $S$, a partition $\pi$ of $S$ (into clusters), and a universe $T$ of tags such that each element in $S$ is associated with a subset of tags, the goal is to find a representative set of tags for each cluster such that those sets are pairwise-disjoint and the total size of all the representatives is minimized. Since this problem is NP-hard in general, we develop approximation algorithms with provable performance guarantees for the problem. We also show applications to explain clusters from datasets, including clusters of genomic sequences that represent different threat levels.

A Graph-Based Approach for Active Learning in Regression

Active learning aims to reduce labeling efforts by selectively asking humans to annotate the most important data points from an unlabeled pool and is an example of human-machine interaction. Though active learning has been extensively researched for classification and ranking problems, it is relatively understudied for regression problems. Most existing active learning for regression methods use the regression function learned at each active learning iteration to select the next informative point to query. This introduces several challenges such as handling noisy labels, parameter uncertainty and overcoming initially biased training data. Instead, we propose a feature-focused approach that formulates both sequential and batch-mode active regression as a novel bipartite graph optimization problem. We conduct experiments on both noise-free and noisy settings. Our experimental results on benchmark data sets demonstrate the effectiveness of our proposed approach.