Identifying and Characterising Higher Order Interactions in Mobility Networks Using Hypergraphs

Understanding human mobility is essential for applications ranging from urban planning to public health. Traditional mobility models such as flow networks and colocation matrices capture only pairwise interactions between discrete locations, overlooking higher-order relationships among locations (i.e., mobility flow among two or more locations). To address this, we propose co-visitation hypergraphs, a model that leverages temporal observation windows to extract group interactions between locations from individual mobility trajectory data. Using frequent pattern mining, our approach constructs hypergraphs that capture dynamic mobility behaviors across different spatial and temporal scales. We validate our method on a publicly available mobility dataset and demonstrate its effectiveness in analyzing city-scale mobility patterns, detecting shifts during external disruptions such as extreme weather events, and examining how a location's connectivity (degree) relates to the number of points of interest (POIs) within it. Our results demonstrate that our hypergraph-based mobility analysis framework is a valuable tool with potential applications in diverse fields such as public health, disaster resilience, and urban planning.

Fair Disaster Containment via Graph-Cut Problems

Graph cut problems form a fundamental problem type in combinatorial optimization, and are a central object of study in both theory and practice. In addition, the study of fairness in Algorithmic Design and Machine Learning has recently received significant attention, with many different notions proposed and analyzed in a variety of contexts. In this paper we initiate the study of fairness for graph cut problems by giving the first fair definitions for them, and subsequently we demonstrate appropriate algorithmic techniques that yield a rigorous theoretical analysis. Specifically, we incorporate two different definitions of fairness, namely demographic and probabilistic individual fairness, in a particular cut problem modeling disaster containment scenarios. Our results include a variety of approximation algorithms with provable theoretical guarantees.

Efficient Algorithms for Generating Provably Near-Optimal Cluster Descriptors for Explainability

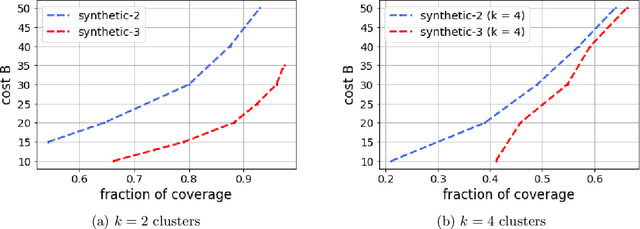
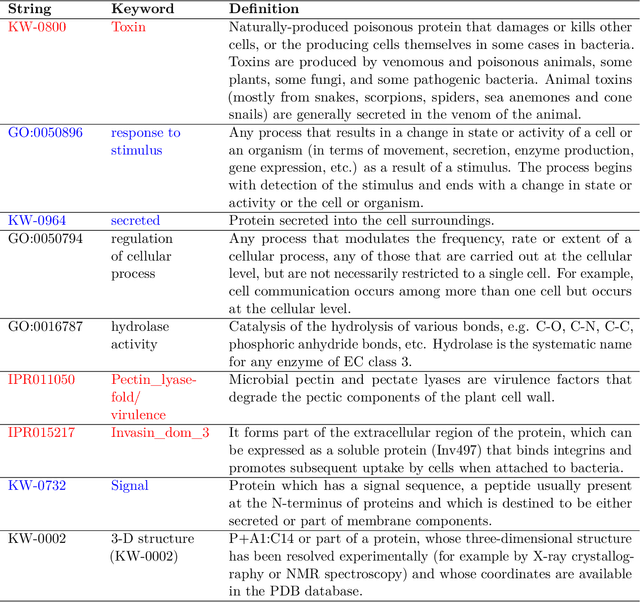
Improving the explainability of the results from machine learning methods has become an important research goal. Here, we study the problem of making clusters more interpretable by extending a recent approach of [Davidson et al., NeurIPS 2018] for constructing succinct representations for clusters. Given a set of objects $S$, a partition $\pi$ of $S$ (into clusters), and a universe $T$ of tags such that each element in $S$ is associated with a subset of tags, the goal is to find a representative set of tags for each cluster such that those sets are pairwise-disjoint and the total size of all the representatives is minimized. Since this problem is NP-hard in general, we develop approximation algorithms with provable performance guarantees for the problem. We also show applications to explain clusters from datasets, including clusters of genomic sequences that represent different threat levels.