Efficient Algorithms for Generating Provably Near-Optimal Cluster Descriptors for Explainability
Paper and Code
Feb 06, 2020

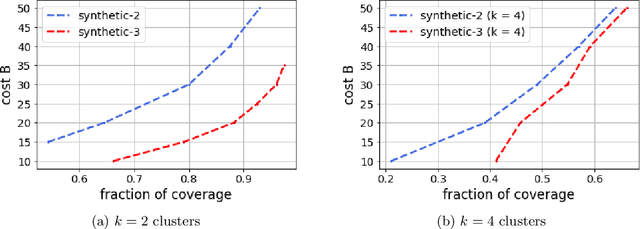
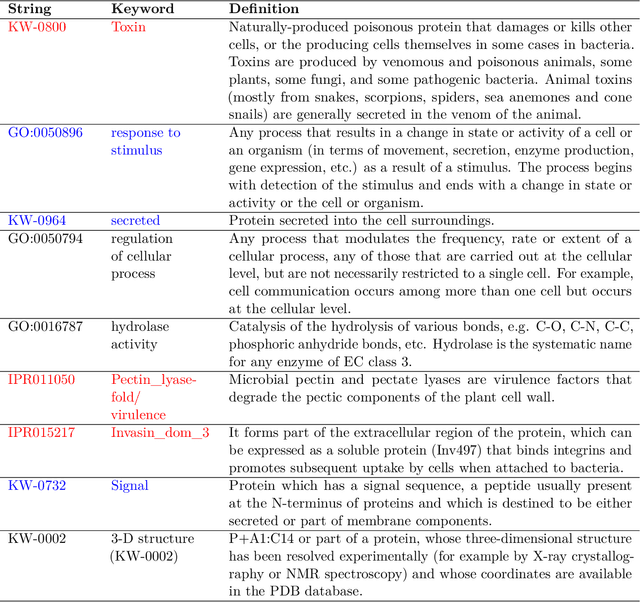
Improving the explainability of the results from machine learning methods has become an important research goal. Here, we study the problem of making clusters more interpretable by extending a recent approach of [Davidson et al., NeurIPS 2018] for constructing succinct representations for clusters. Given a set of objects $S$, a partition $\pi$ of $S$ (into clusters), and a universe $T$ of tags such that each element in $S$ is associated with a subset of tags, the goal is to find a representative set of tags for each cluster such that those sets are pairwise-disjoint and the total size of all the representatives is minimized. Since this problem is NP-hard in general, we develop approximation algorithms with provable performance guarantees for the problem. We also show applications to explain clusters from datasets, including clusters of genomic sequences that represent different threat levels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge